Conversores de código: BCD (8421) a/desde Excess-3 – Part 1

Requisito previo: sistema numérico y conversiones de base 

El código binario Excess-3 es un código BCD  autocomplementario no ponderado .
La propiedad autocomplementaria significa que el complemento a 1 de un número en exceso de 3 es el código en exceso de 3 del complemento a 9 del número decimal correspondiente. Esta propiedad es útil ya que un número decimal puede complementarse con nueves (para la resta) tan fácilmente como un número binario puede complementarse con unos; simplemente invirtiendo todos los bits. 
Por ejemplo, el código de exceso-3 para 3(0011) es 0110, y para encontrar el código de exceso-3 del complemento de 3, solo necesitamos encontrar el complemento a 1 de 0110 -> 1001, que también es el exceso- 3 código para el complemento a 9 de 3 -> (9-3) = 6.  

Convertir BCD(8421) a Exceso-3 –

Como su nombre lo indica claramente, un dígito BCD se puede convertir a su correspondiente código Excess-3 simplemente agregándole 3. Como solo tenemos 10 dígitos (0 a 9) en decimal, no nos importa el resto y los marcamos con una cruz (X).
Sean  los bits que representan los números binarios, donde  está el LSB y  el MSB, y 
Sean  los bits que representan el código gris de los números binarios, donde  está el LSB y  el MSB. 
La tabla de verdad para la conversión se da a continuación. La marca de la X es la condición de no importa. 
 

Para encontrar el circuito digital correspondiente, utilizaremos la técnica K-Map para cada uno de los bits del código Excess-3 como salida con todos los bits del número BCD como entrada.

Expresiones booleanas minimizadas correspondientes para Excess-3 bits de código –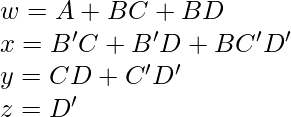 

El circuito digital correspondiente- 
 

Conversión de Exceso-3 a BCD (8421) –

El código Excess-3 se puede volver a convertir a BCD de la misma manera. 
Sean  los bits que representan los números binarios, donde  está el LSB y  el MSB, y 
Sean  los bits que representan el código gris de los números binarios, donde  está el LSB y  el MSB. 
La tabla de verdad para la conversión se da a continuación. La marca de la X es la condición de no importa. 
 

Mapa K para D- 

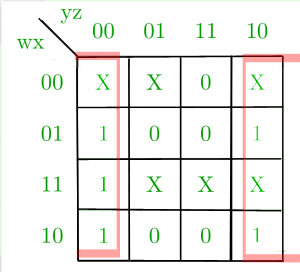
Mapa K para C- 

Mapa K para B- 

K-Map para A- 
<img src=”

 
Expresiones booleanas minimizadas correspondientes para Excess-3 bits de código –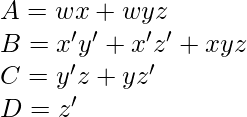 

El circuito digital correspondiente – 
Aquí  corresponden a  y  corresponden a  . 

 Este artículo es una contribución de Chirag Manwani . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks. 

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.