Espacio afín – Barcelona Geeks

Espacios afines

Espacio afín

Espacio afín es el conjunto E con espacio vectorial \vec{E} y una acción transitiva y libre del aditivo \vec{E} sobre el conjunto E. Los elementos del espacio A se llaman puntos. El espacio vectorial \vec{E} que está asociado con el espacio afín se conoce como vectores libres y la acción +: E * \vec{E} \rightarrow E cumple las siguientes condiciones:

Identidad Correcta: a + 0 = a $\, \forall \, a \,\epsilon \,A$
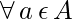
Asociatividad: $(a + u) + v = a + (u+v) \, \forall a \, \epsilon \, E \,\, \forall \, \, u, v \, \epsilon \, \vec{E}$
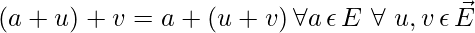
Para cualesquiera dos puntos a,b \epsilon E, existe un único u tal que:

$a + u =b$

donde u \epsilon \vec{E} y se puede denotar como ab o \vec{ab} oa veces como ba. Por lo tanto, podemos escribir la ecuación anterior

$b= a + ab$

Ejemplo:

. Considere el subconjunto L de $A^2$ que consta de todos los puntos (x, y) que satisfacen la ecuación:

$x+y - 1=0$

L es la recta de pendiente -1 que pasa por el punto (1,0) y (0,1). La línea L puede ser un espacio afín definiendo la acción +: L * R \rightarrow L de R sobre L definida de tal manera que todo punto (x, 1-x) sobre L y cualquier u \epsilon R.

$(x, 1-x) + u = (x+u, 1-x-u)$

Ahora, para dos puntos cualesquiera a =(a_1, 1- a_1) y b = (b_1, 1-b_1) en L, el único vector u \epsilon R tal que b = a+u es u = b_1 – a_1. Tenga en cuenta que el espacio vectorial R es isomorfo a la línea de ecuación x + y = 0 que pasa por el origen.

Identidad de Chasles

Dados tres puntos cualesquiera $a,b,c \epsilon$ , dado que c = a + ac, b = a + ab y c = b + bc, obtenemos

$c = b+ bc = a + ab +bc$

Aplicando las propiedades 2 y 3 anteriores,

$ab +bc = ac$

La ecuación anterior se conoce como identidad de Chasles. Ya que

a = a + aa

y usando la propiedad 1 obtenemos

a = a+ 0

Así, usando la propiedad 3, obtenemos:

$aa=0$

Reemplazando a en lugar de c en Chasles Identity, obtenemos:

ba =-ab

Ahora, para 4 puntos a,b,c,d \epsilon E. La identidad de chasles se puede dar como:

ad+bc = ad+ dc = ac

Combinaciones afines/ Baricentros

Similar a la combinación lineal en álgebra lineal, el concepto correspondiente en geometría afín es el de una combinación afín, también llamada baricentro.

Considere el espacio bidimensional como un espacio afín, con origen O= (0,0) y vectores base (1,0) y (0,1). Dados dos puntos cualesquiera a =(a1, a2) y b =(b1, b2) puede haber una combinación natural tal que \lambda a+ \mu b o:

$(\lambda a_1 + \mu b_1, \lambda a_2 + \mu b_2)$

cuando a = (-1, -1) yb = (2, 2), entonces a+b se puede dar como: c = (1,1).

Ahora, considere el nuevo sistema de coordenadas con respecto al origen c = (1, 1). Ahora, las coordenadas de a = (-2, -2), las coordenadas de b son (1, 1), y el punto de d = (-1, -1). Sin embargo, el punto d es idéntico al origen O = (0, 0) del primer sistema de coordenadas.

Así, a + b corresponde a dos puntos distintos según el sistema de coordenadas que se utilice para su cálculo. Esto significa que necesitamos condiciones adicionales para cálculos afines. Resulta que los escalares suman 1. Esto nos ayuda a definir los Baricentros

Para cualquier familia de puntos (a_i)_{i\epsilon I} en E, para cualquier familia de escalares tal que $\sum_{i \epsilon I } \lambda_i =1$ y para cualquier $a \epsilon E$ , el punto

$a + \sum_{i \epsilon I} \lambda_i a a_i$ is called the barycentres of the points a_i assigned the weights $\lambda_i$ and is denoted by:

$\sum_{i \epsilon E} \lambda_i a_i$ .

Los baricentros se denotan convenientemente mediante las notaciones $(a, \lambda)$ , mientras que $a \epsilon E$ es un punto y $\lambda \epsilon R$ se denomina escalar.

Subespacio afín

V es el subespacio afín de $\vec{E}$ en la dirección de $\vec{V}$

Dado un espacio afín $\left \langle E, \vec{E}, + \right \rangle$ , un subconjunto V de E es un subespacio afín de $\left \langle E, \vec{E}, + \right \rangle$ , si para toda familia de puntos ponderados $((ai , λi))_{i \epsilon I}$ en V tal que $\sum_{i \epsilon I} \lambda_i = 1$ , el baricentro $\sum_{i \epsilon I } \lambda_{i} a_i$ pertenece a V .