ML | Ecuación Normal en Regresión Lineal

La ecuación normal es un enfoque analítico de la regresión lineal con una función de costo de mínimos cuadrados. Podemos averiguar directamente el valor de θ sin usar Gradient Descent . Seguir este enfoque es una opción eficaz y que ahorra tiempo cuando se trabaja con un conjunto de datos con características pequeñas. El método de ecuación normal se basa en el concepto matemático de máximos y mínimos en el que la derivada y la derivada parcial de cualquier función serían cero en el punto mínimo y máximo. Entonces, en el método de Ecuación Normal, obtenemos el valor mínimo de la función de Costo encontrando su derivada parcial con respecto a cada peso e igualándola a cero.

La ecuación normal es la siguiente:

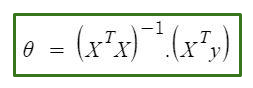
En la ecuación anterior, 

θ: parámetros de la hipótesis que mejor la definen. 
X: valor de característica de entrada de cada instancia. 
Y: valor de salida de cada instancia. 

Matemáticas Detrás de la ecuación:

Dada la función de hipótesis 

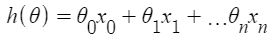
donde, 
n: el no. de características en el conjunto de datos. 
x ₀ : 1 (para la multiplicación de vectores) 
Tenga en cuenta que este es un producto escalar entre los valores de θ y x. Entonces, para la conveniencia de resolver, podemos escribirlo como:

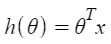
El motivo de la Regresión Lineal es minimizar la función de costo : 

donde, 
x ⁱ : el valor de entrada del ejemplo de entrenamiento  i ^{ih .}
m: no de instancias de entrenamiento 
n: no. de características del conjunto de datos 
y ⁱ : el resultado esperado de i ^-ésima instancia 

Representemos la función de costo en forma vectorial.

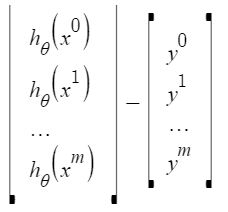
Hemos ignorado 1/2m aquí ya que no hará ninguna diferencia en el funcionamiento. Se usó por conveniencia matemática al calcular el descenso del gradiente. Pero ya no es necesario aquí. 

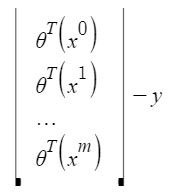
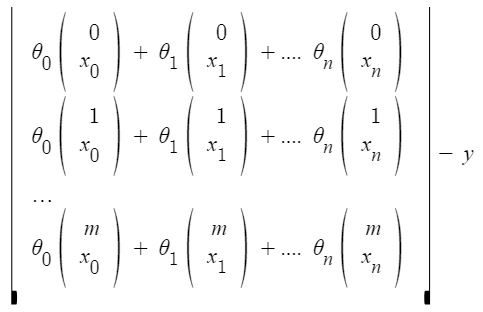
x ⁱ _j : valor de la característica j ^ih en el ejemplo de entrenamiento  i ^{ih .}

Esto puede reducirse aún más a 

Pero cada valor residual se eleva al cuadrado. No podemos simplemente elevar al cuadrado la expresión anterior. Como el cuadrado de un vector/array no es igual al cuadrado de cada uno de sus valores. Entonces, para obtener el valor al cuadrado, multiplique el vector/array con su transpuesta. Entonces, la ecuación final derivada es 

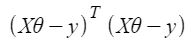
Por lo tanto, la función de costo es 

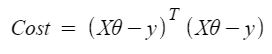
Entonces, ahora obteniendo el valor de θ usando la derivada parcial 

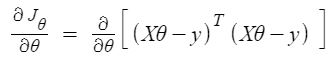
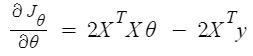
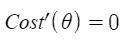
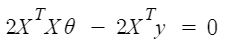
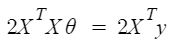
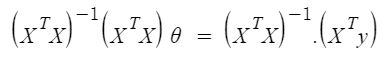
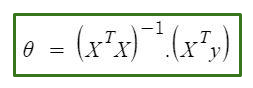
Entonces, esta es la Ecuación Normal finalmente derivada con θ dando el valor de costo mínimo.

Ejemplo:

# This code may not run on GFG IDE
# as required modules not found.
 
# import required modules
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
 
# Create data set.
x, y = make_regression(n_samples=100, n_features=1,
                       n_informative=1, noise=10, random_state=10)
 
# Plot the generated data set.
plt.scatter(x, y, s=30, marker='o')
plt.xlabel("Feature_1 --->")
plt.ylabel("Target_Variable --->")
plt.title('Simple Linear Regression')
plt.show()
 
# Convert  target variable array from 1d to 2d.
y = y.reshape(100, 1)

Producción:

Implementemos la Ecuación Normal:

# code
 
# Adding x0=1 to each instance
x_new = np.array([np.ones(len(x)), x.flatten()]).T
 
# Using Normal Equation.
theta_best_values = np.linalg.inv(x_new.T.dot(x_new)).dot(x_new.T).dot(y)
 
# Display best values obtained.
print(theta_best_values)

[[ 0.52804151]
 [30.65896337]]

Intente predecir para una nueva instancia de datos:

# sample data instance.
x_sample = np.array([[-2], [4]])
 
# Adding x0=1 to each instance.
x_sample_new = np.array([np.ones(len(x_sample)), x_sample.flatten()]).T
 
# Display the sample.
print("Before adding x0:\n", x_sample)
print("After adding x0:\n", x_sample_new)

Before adding x0:
 [[-2]
 [ 4]]
After adding x0:
 [[ 1. -2.]
 [ 1.  4.]]

# code
# predict the values for given data instance.
predict_value=x_sample_new.dot(theta_best_values)
print(predict_value)

[[-60.78988524]
 [123.16389501]]

Trazar la salida:

# code
 
# Plot the output.
plt.scatter(x,y,s=30,marker='o')
plt.plot(x_sample,predict_value,c='red')
plt.plot()
plt.xlabel("Feature_1 --->")
plt.ylabel("Target_Variable --->")
plt.title('Simple Linear Regression')
plt.show()

Verifique lo anterior usando la clase sklearn LinearRegression:

# code
 
# Verification.
from sklearn.linear_model import LinearRegression
lr=LinearRegression()    # Object.
lr.fit(x,y)              # fit method.
 
# Print obtained theta values.
print("Best value of theta:",lr.intercept_,lr.coef_,sep='\n')
 
#predict.
print("predicted value:",lr.predict(x_sample),sep='\n')

Best value of theta:
[0.52804151]
[[30.65896337]]

predicted value:
[[-60.78988524]
 [123.16389501]]