Raíz cuadrada inversa rápida

La raíz cuadrada inversa rápida es un algoritmo que estima  , el recíproco (o inverso multiplicativo) de la raíz cuadrada de un número de punto flotante de 32 bits x en formato de punto flotante IEEE 754. Calcular raíces cuadradas recíprocas es necesario en muchas aplicaciones, como la normalización de vectores en videojuegos y se usa principalmente en cálculos relacionados con la programación 3D. En gráficos 3D, normales de superficie, se utilizan vectores de 3 coordenadas de longitud 1 para expresar la iluminación y la reflexión. Había muchas superficies normales. Y calcularlos implica normalizar muchos vectores. La normalización es a menudo solo un término elegante para la división. El teorema de Pitágoras calcula la distancia entre puntos, y dividir por la distancia ayuda a normalizar los vectores: 
este algoritmo es mejor conocido por su implementación en 1999 en el código fuente deQuake III Arena Game , un videojuego de disparos en primera persona que hizo un uso intensivo de gráficos en 3D. En ese momento, generalmente era computacionalmente costoso calcular el recíproco de un número de coma flotante, especialmente a gran escala; la raíz cuadrada inversa rápida omitió este paso. Algoritmo: Paso 1: Reinterpreta los bits de la entrada de coma flotante como un número entero.

i  = * ( long * ) &y; 

Paso 2: toma el valor resultante y realiza operaciones aritméticas enteras que producen una aproximación del valor que estamos buscando.

i  = 0x5f3759df - ( i >> 1 );

Paso 3: Sin embargo, el resultado no es la aproximación en sí, es un número entero que resulta ser, si reinterpreta los bits como un número de coma flotante, la aproximación. Entonces, el código hace lo contrario de la conversión en el paso 1 para volver al punto flotante:

y  = * ( float * ) &i;

Paso 4: Y finalmente ejecuta una única iteración del método de Newton para mejorar la aproximación.

y  = y * ( threehalfs - ( x2 * y * y ) );         //threehalfs = 1.5F;

El algoritmo acepta un número de coma flotante de 32 bits como entrada y almacena un valor reducido a la mitad para su uso posterior. Luego, al tratar los bits que representan el número de coma flotante como un número entero de 32 bits, se realiza un desplazamiento lógico de un bit a la derecha y el resultado se resta del número mágico 0x5F3759DF. Esta es la primera aproximación de la raíz cuadrada inversa de la entrada. Tratando los bits nuevamente como un número de coma flotante, ejecuta una iteración del método de aproximación de Newton, lo que produce una aproximación más precisa. Digamos que hay un número en forma de exponente o notación científica:             = 100 millones Ahora, para encontrar la raíz cuadrada regular, simplemente dividiríamos el exponente entre 2:         Y si, quieres saber la raíz cuadrada inversa, dividimos el exponente entre -2 para voltear el signo: 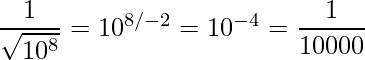       Entonces, el código convierte el número de coma flotante en un número entero. Luego cambia los bits por uno, lo que significa que los bits del exponente se dividen por 2 (cuando eventualmente volvemos a convertir los bits en un flotador). Y por último, para negar el exponente, restamos del número mágico 0x5f3759df. Esto hace algunas cosas: conserva la mantisa (la parte no exponente, también conocida como 5 en: 5 ·  ), maneja exponentes pares e impares, cambia bits del exponente a la mantisa y todo tipo de cosas divertidas. El siguiente código es la implementación de raíz cuadrada inversa rápida de Quake III Arena (comentario original exacto escrito en Quake III Arena Game). 

// CPP program for fast inverse square root.
#include<bits/stdc++.h>
using namespace std;
 
// function to find the inverse square root
float inverse_rsqrt( float number )
{
 const float threehalfs = 1.5F;
 
 float x2 = number * 0.5F;
 float y = number;
  
 // evil floating point bit level hacking
 long i = * ( long * ) &y;
  
 // value is pre-assumed
 i = 0x5f3759df - ( i >> 1 );
 y = * ( float * ) &i;
  
 // 1st iteration
 y = y * ( threehalfs - ( x2 * y * y ) );
  
 // 2nd iteration, this can be removed
 // y = y * ( threehalfs - ( x2 * y * y ) );
 
 return y;
}
 
// driver code
int main(){
  
 int n = 256;
 float f = inverse_rsqrt(n);
 cout << f << endl;
  
 return 0;
}

Producción :

0.0623942

Complejidad de tiempo: O(1)
Complejidad de espacio: O(1)