Número máximo de aristas en gráfico bipartito

Dado un número entero N que representa el número de vértices. La tarea es encontrar el máximo número de aristas posibles en un gráfico bipartito de N vértices.
Gráfica bipartita: 
 

1. Un grafo bipartito es aquel que tiene 2 conjuntos de vértices.
2. Los conjuntos son tales que los vértices del mismo conjunto nunca compartirán una arista entre ellos.

Ejemplos: 
 

Entrada: N = 10 
Salida: 25 
Ambos conjuntos contendrán 5 vértices y cada vértice del primer conjunto 
tendrá una arista con todos los demás vértices del segundo conjunto, 
es decir, aristas totales = 5 * 5 = 25
Entrada: N = 9 
Salida: 20 
 

Enfoque: El número de aristas será máximo cuando cada vértice de un conjunto dado tenga una arista con todos los demás vértices del otro conjunto, es decir, aristas = m * n donde m y n son el número de aristas en ambos conjuntos. para maximizar el número de aristas, m debe ser igual o lo más cercano posible a n . Por lo tanto, el número máximo de aristas se puede calcular con la fórmula, 
 

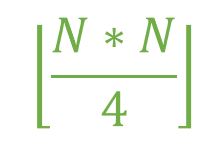
A continuación se muestra la implementación del enfoque anterior: 
 

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to return the maximum number
// of edges possible in a Bipartite
// graph with N vertices
int maxEdges(int N)
{
    int edges = 0;
 
    edges = floor((N * N) / 4);
 
    return edges;
}
 
// Driver code
int main()
{
    int N = 5;
    cout << maxEdges(N);
 
    return 0;
}

// Java implementation of the approach
 
class GFG {
 
    // Function to return the maximum number
    // of edges possible in a Bipartite
    // graph with N vertices
    public static double maxEdges(double N)
    {
        double edges = 0;
 
        edges = Math.floor((N * N) / 4);
 
        return edges;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        double N = 5;
        System.out.println(maxEdges(N));
    }
}
 
// This code is contributed by Naman_Garg.

# Python3 implementation of the approach
 
# Function to return the maximum number
# of edges possible in a Bipartite
# graph with N vertices
def maxEdges(N) :
 
    edges = 0;
 
    edges = (N * N) // 4;
 
    return edges;
 
# Driver code
if __name__ == "__main__" :
     
    N = 5;
    print(maxEdges(N));
 
# This code is contributed by AnkitRai01

// C# implementation of the approach
using System;
 
class GFG {
 
    // Function to return the maximum number
    // of edges possible in a Bipartite
    // graph with N vertices
    static double maxEdges(double N)
    {
        double edges = 0;
 
        edges = Math.Floor((N * N) / 4);
 
        return edges;
    }
 
    // Driver code
    static public void Main()
    {
        double N = 5;
        Console.WriteLine(maxEdges(N));
    }
}
 
// This code is contributed by jit_t.

<?php
// PHP implementation of the approach
 
// Function to return the maximum number
// of edges possible in a Bipartite
// graph with N vertices
 
function maxEdges($N)
{
    $edges = 0;
 
    $edges = floor(($N * $N) / 4);
 
    return $edges;
}
 
// Driver code
    $N = 5;
    echo maxEdges($N);
 
// This code is contributed by ajit.
?>

<script>
 
// Javascript implementation of the approach
 
// Function to return the maximum number
// of edges possible in a Bipartite
// graph with N vertices
function maxEdges(N)
{
    var edges = 0;
 
    edges = Math.floor((N * N) / 4);
 
    return edges;
}
 
// Driver code
var N = 5;
document.write( maxEdges(N));
 
</script>

6

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)