Dados dos números complejos Z1 y Z2 en forma cartesiana , la tarea es convertir el número complejo dado en forma polar y realizar todas las operaciones aritméticas (suma, resta, multiplicación y división) sobre ellos.
Ejemplos:
Entrada: Z1 = (2, 3), Z2 = (4, 6)
Salida:
Forma polar del primer número complejo: (3,605551275463989, 0,9827937232473292)
Forma polar del segundo número complejo: (7,211102550927978, 0,9827937232473292)
Suma de dos números complejos : (10.816653826391967, 0.9827937232473292)
resta de dos números complejos: (3.605551275463989, -0.98293723232473292)
Multiplicación de dos números complejos: (25.9999999999999996,
1.964444444444444442844444444444ESTACIÓNEntrada: Z1 = (1, 1), Z2 = (2, 2)
Salida:
Forma polar del primer número complejo: (1,4142135623730951, 0,7853981633974482)
Forma polar del segundo número complejo: (2,8284271247461903, 0,7853981633974482)
Suma de dos números complejos : (4.242640687119286, 0.78539816339744482)
resta de dos números complejos: (1.4142135623730951, -0.785398163339744482)
Multiplicación de dos números complejos: (4.0000000000000000001, 1.57079639639696969696963
)
Enfoque: El problema dado se puede resolver en base a las siguientes propiedades de los Números Complejos:
- Un número complejo Z en forma cartesiana se representa como:
,
donde a, b € R y b se conoce como la parte imaginaria del número complejo y
- La forma polar del número complejo Z es:
donde, r se conoce como módulos de un número complejo y
es el ángulo que forma con el eje X positivo.
- En la expresión de número complejo en forma polar tomando r como común realizando
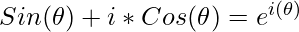 la expresión se convierte en:
la expresión se convierte en:
 , que se conoce como la forma Euleriana del Número Complejo .
, que se conoce como la forma Euleriana del Número Complejo .- Las formas euleriana y polar se representan como:
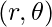 .
.
- La multiplicación y división de dos números complejos se puede hacer usando la forma euleriana:
Para la multiplicación:
=>Por División:
=>
Siga los pasos a continuación para resolver el problema:
- Convierta los números complejos en polares usando la fórmula discutida anteriormente e imprímala en el formulario para
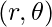 .
. - Defina una función, digamos Suma (Z1, Z2) para realizar la operación de suma:
- Encuentre la parte real del número complejo sumando dos partes reales Z1 y Z2, y guárdela en una variable, digamos a .
- Encuentre la parte imaginaria del número complejo sumando dos partes imaginarias de los números complejos Z1 y Z2 y guárdela en una variable, digamos b .
- Convierta la forma cartesiana del complejo a forma polar e imprímala.
- Defina una función, digamos Subtraction(Z1, Z2) para realizar la operación de resta:
- Encuentre la parte real del número complejo restando dos partes reales Z1 y Z2, y guárdela en una variable, digamos a.
- Encuentre la parte imaginaria del número complejo restando dos partes imaginarias de los números complejos Z1 y Z2 y guárdela en una variable, digamos b.
- Convierta la forma cartesiana del complejo a forma polar e imprímala.
- Imprime la multiplicación de dos números complejos Z1 y Z2 como
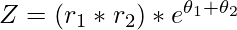
- Imprime la división de dos números complejos Z1 y Z2 como
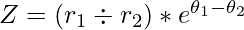
A continuación se muestra la implementación del enfoque anterior:
Python3
# Python program for the above approach
import math
# Function to find the polar form
# of the given Complex Number
def get_polar_form(z):
# Z is in cartesian form
re, im = z
# Stores the modulo of complex number
r = (re * re + im * im) ** 0.5
# If r is greater than 0
if r:
theta = math.asin(im / r)
return (r, theta)
# Otherwise
else:
return (0, 0)
# Function to add two complex numbers
def Addition(z1, z2):
# Z is in polar form
r1, theta1 = z1
r2, theta2 = z2
# Real part of complex number
a = r1 * math.cos(theta1) + r2 * math.cos(theta2)
# Imaginary part of complex Number
b = r1 * math.sin(theta1) + r2 * math.sin(theta2)
# Find the polar form
return get_polar_form((a, b))
# Function to subtract two
# given complex numbers
def Subtraction(z1, z2):
# Z is in polar form
r1, theta1 = z1
r2, theta2 = z2
# Real part of the complex number
a = r1 * math.cos(theta1) - r2 * math.cos(theta2)
# Imaginary part of complex number
b = r1 * math.sin(theta1) - r2 * math.sin(theta2)
# Converts (a, b) to polar
# form and return
return get_polar_form((a, b))
# Function to multiply two complex numbers
def Multiplication(z1, z2):
# z is in polar form
r1, theta1 = z1
r2, theta2 = z2
# Return the multiplication of Z1 and Z2
return (r1 * r2, theta1 + theta2)
# Function to divide two complex numbers
def Division(z1, z2):
# Z is in the polar form
r1, theta1 = z1
r2, theta2 = z2
# Return the division of Z1 and Z2
return (r1 / r2, theta1-theta2)
# Driver Code
if __name__ == "__main__":
z1 = (2, 3)
z2 = (4, 6)
# Convert into Polar Form
z1_polar = get_polar_form(z1)
z2_polar = get_polar_form(z2)
print("Polar form of the first")
print("Complex Number: ", z1_polar)
print("Polar form of the Second")
print("Complex Number: ", z2_polar)
print("Addition of two complex")
print("Numbers: ", Addition(z1_polar, z2_polar))
print("Subtraction of two ")
print("complex Numbers: ",
Subtraction(z1_polar, z2_polar))
print("Multiplication of two ")
print("Complex Numbers: ",
Multiplication(z1_polar, z2_polar))
print("Division of two complex ")
print("Numbers: ", Division(z1_polar, z2_polar))
Javascript
// JavaScript program for the above approach
// Function to find the polar form
// of the given Complex Number
function get_polar_form(z){
// Z is in cartesian form
let re = z[0];
let im = z[1];
// Stores the modulo of complex number
let r = (re * re + im * im) ** 0.5;
// If r is greater than 0
if(r){
let theta = Math.asin(im / r);
return [r, theta];
}
// Otherwise
else{
return [0, 0];
}
}
// Function to add two complex numbers
function Addition(z1, z2){
// Z is in polar form
let r1 = z1[0];
let theta1 = z1[1];
let r2 = z2[0];
let theta2 = z2[1];
// console.log(r1, r2, theta1, theta2)
// Real part of complex number
let a = r1 * Math.cos(theta1) + r2 * Math.cos(theta2);
// Imaginary part of complex Number
let b = r1 * Math.sin(theta1) + r2 * Math.sin(theta2);
console.log(a, b)
// Find the polar form
return get_polar_form([a, b]);
}
// Function to subtract two
// given complex numbers
function Subtraction(z1, z2){
// Z is in polar form
let r1 = z1[0];
let theta1 = z1[1];
let r2 = z2[0];
let theta2 = z2[1];
// Real part of the complex number
let a = r1 * Math.cos(theta1) - r2 * Math.cos(theta2);
// Imaginary part of complex number
let b = r1 * Math.sin(theta1) - r2 * Math.sin(theta2);
// Converts (a, b) to polar
// form and return
return get_polar_form([a, b]);
}
// Function to multiply two complex numbers
function Multiplication(z1, z2){
// z is in polar form
let r1 = z1[0];
let theta1 = z1[1];
let r2 = z2[0];
let theta2 = z2[1];
// Return the multiplication of Z1 and Z2
return [r1 * r2, theta1 + theta2];
}
// Function to divide two complex numbers
function Division(z1, z2){
// Z is in the polar form
let r1 = z1[0];
let theta1 = z1[1];
let r2 = z2[0];
let theta2 = z2[1];
// Return the division of Z1 and Z2
return [r1 / r2, theta1-theta2];
}
// Driver Code
z1 = [2, 3];
z2 = [4, 6];
// Convert into Polar Form
z1_polar = get_polar_form(z1)
z2_polar = get_polar_form(z2)
console.log("Polar form of the first");
console.log("Complex Number: ", z1_polar);
console.log("Polar form of the Second");
console.log("Complex Number: ", z2_polar);
console.log("Addition of two complex");
console.log("Numbers: ", Addition(z1_polar, z2_polar));
console.log("Subtraction of two ");
console.log("complex Numbers: ",
Subtraction(z1_polar, z2_polar));
console.log("Multiplication of two ");
console.log("Complex Numbers: ",
Multiplication(z1_polar, z2_polar));
console.log("Division of two complex ");
console.log("Numbers: ", Division(z1_polar, z2_polar));
// The code is contributed by Gautam goel (gautamgoel962)
Polar form of the first Complex Number: (3.605551275463989, 0.9827937232473292) Polar form of the Second Complex Number: (7.211102550927978, 0.9827937232473292) Addition of two complex Numbers: (10.816653826391967, 0.9827937232473292) Subtraction of two complex Numbers: (3.605551275463989, -0.9827937232473292) Multiplication of two Complex Numbers: (25.999999999999996, 1.9655874464946583) Division of two complex Numbers: (0.5, 0.0)
Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)