ML | Búsqueda de árboles de Monte Carlo (MCTS)

Monte Carlo Tree Search (MCTS) es una técnica de búsqueda en el campo de la Inteligencia Artificial (IA). Es un algoritmo de búsqueda heurístico y probabilístico que combina las implementaciones clásicas de búsqueda de árboles junto con los principios de aprendizaje automático del aprendizaje por refuerzo.
En la búsqueda de árbol, siempre existe la posibilidad de que la mejor acción actual en realidad no sea la acción más óptima. En tales casos, el algoritmo MCTS se vuelve útil ya que continúa evaluando otras alternativas periódicamente durante la fase de aprendizaje ejecutándolas, en lugar de la estrategia óptima percibida actual. Esto se conoce como el “ trade-off de exploración-explotación”.“. Explota las acciones y estrategias que se encuentran como las mejores hasta ahora, pero también debe continuar explorando el espacio local de decisiones alternativas y averiguar si podrían reemplazar a las mejores actuales.
La exploración ayuda a explorar y descubrir las partes inexploradas del árbol, lo que podría resultar en encontrar un camino más óptimo. En otras palabras, podemos decir que la exploración expande el ancho del árbol más que su profundidad. La exploración puede ser útil para garantizar que MCTS no pase por alto ningún camino potencialmente mejor. Pero rápidamente se vuelve ineficiente en situaciones con gran cantidad de pasos o repeticiones. Para evitarlo, se compensa con la explotación. La explotación se apega a un solo camino que tiene el mayor valor estimado. Este es un enfoque codicioso y esto extenderá la profundidad del árbol más que su ancho. En palabras simples, 
Por esta característica, MCTS se vuelve particularmente útil para tomar decisiones óptimas en problemas de Inteligencia Artificial (IA). 
  
Algoritmo Monte Carlo Tree Search (MCTS): 
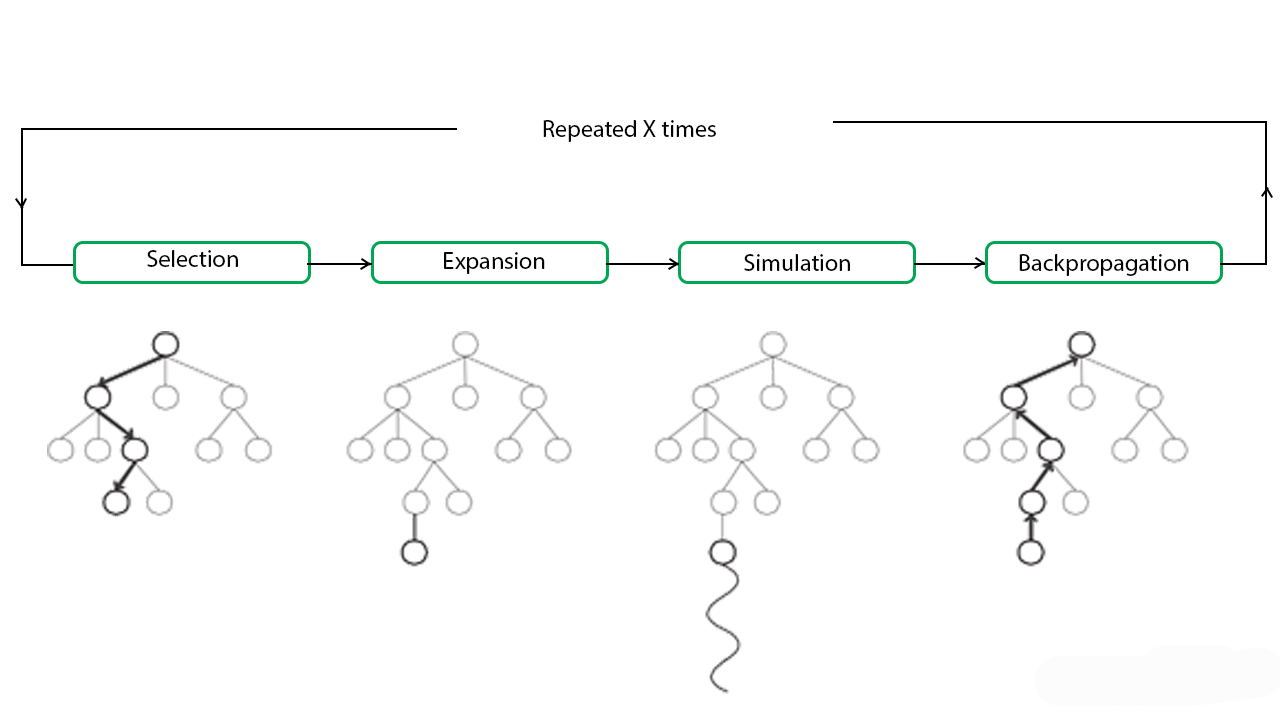
en MCTS, los Nodes son los componentes básicos del árbol de búsqueda. Estos Nodes se forman en función del resultado de una serie de simulaciones. El proceso de Monte Carlo Tree Search se puede dividir en cuatro pasos distintos, a saber, selección, expansión, simulación y retropropagación. Cada uno de estos pasos se explica en detalle a continuación: 
 

• Selección: en este proceso, el algoritmo MCTS atraviesa el árbol actual desde el Node raíz utilizando una estrategia específica. La estrategia utiliza una función de evaluación para seleccionar de manera óptima los Nodes con el valor estimado más alto. MCTS utiliza la fórmula Upper Confidence Bound (UCB) aplicada a los árboles como estrategia en el proceso de selección para atravesar el árbol. Equilibra el equilibrio entre exploración y explotación. Durante el recorrido del árbol, se selecciona un Node en función de algunos parámetros que devuelven el valor máximo. Los parámetros se caracterizan por la fórmula que se suele utilizar para este fin, que se indica a continuación. 
   

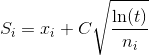
• dónde; 
  S _i = valor de un Node i 
  x _i = media empírica de un Node i 
  C = una constante 
  t = número total de simulaciones
  Al atravesar un árbol durante el proceso de selección, el Node hijo que arroja el mayor valor de la ecuación anterior será uno que será seleccionado. Durante el recorrido, una vez que se encuentra un Node secundario que también es un Node hoja, el MCTS salta al paso de expansión.
• Expansión: en este proceso, se agrega un nuevo Node secundario al árbol a ese Node que se alcanzó de manera óptima durante el proceso de selección.
• Simulación: En este proceso, se realiza una simulación eligiendo movimientos o estrategias hasta lograr un resultado o estado predefinido.
• Backpropagation: después de determinar el valor del Node recién agregado, el árbol restante debe actualizarse. Por lo tanto, se realiza el proceso de retropropagación, donde se retropropaga desde el nuevo Node hasta el Node raíz. Durante el proceso, se incrementa el número de simulaciones almacenadas en cada Node. Además, si la simulación del nuevo Node da como resultado una victoria, el número de victorias también se incrementa.

Los pasos anteriores se pueden entender visualmente por el diagrama que se muestra a continuación: 
 

Estos tipos de algoritmos son particularmente útiles en juegos basados ​​en turnos donde no hay ningún elemento de azar en la mecánica del juego, como Tic Tac Toe, Connect 4, Checkers, Chess, Go, etc. Esto ha sido utilizado recientemente por programas de inteligencia artificial como AlphaGo, para jugar contra los mejores jugadores de Go del mundo. Pero, su aplicación no se limita solo a los juegos. Se puede utilizar en cualquier situación descrita por pares de estado-acción y simulaciones utilizadas para pronosticar resultados.
Pseudocódigo para la búsqueda del árbol de Monte Carlo: 
 

# main function for the Monte Carlo Tree Search
def monte_carlo_tree_search(root):
     
    while resources_left(time, computational power):
        leaf = traverse(root)
        simulation_result = rollout(leaf)
        backpropagate(leaf, simulation_result)
         
    return best_child(root)
 
# function for node traversal
def traverse(node):
    while fully_expanded(node):
        node = best_uct(node)
         
    # in case no children are present / node is terminal
    return pick_unvisited(node.children) or node
 
# function for the result of the simulation
def rollout(node):
    while non_terminal(node):
        node = rollout_policy(node)
    return result(node)
 
# function for randomly selecting a child node
def rollout_policy(node):
    return pick_random(node.children)
 
# function for backpropagation
def backpropagate(node, result):
    if is_root(node) return
    node.stats = update_stats(node, result)
    backpropagate(node.parent)
 
# function for selecting the best child
# node with highest number of visits
def best_child(node):
    pick child with highest number of visits

Como podemos ver, el algoritmo MCTS se reduce a un conjunto muy reducido de funciones que podemos utilizar en cualquier elección de juegos o en cualquier estrategia de optimización.
Ventajas de la búsqueda de árboles de Monte Carlo: 
 

1. MCTS es un algoritmo simple de implementar.
2. Monte Carlo Tree Search es un algoritmo heurístico. MCTS puede operar de manera efectiva sin ningún conocimiento en el dominio particular, además de las reglas y las condiciones finales, y puede encontrar sus propios movimientos y aprender de ellos jugando playouts aleatorios.
3. El MCTS se puede guardar en cualquier estado intermedio y ese estado se puede usar en casos de uso futuros cuando sea necesario.
4. MCTS admite la expansión asimétrica del árbol de búsqueda en función de las circunstancias en las que opera.

Desventajas de la búsqueda de árboles Monte Carlo: 
 

1. Como el crecimiento del árbol se vuelve rápido después de algunas iteraciones, requiere una gran cantidad de memoria.
2. Hay un pequeño problema de confiabilidad con Monte Carlo Tree Search. En ciertos escenarios, puede haber una sola rama o camino, que puede conducir a la pérdida contra la oposición cuando se implementa para esos juegos por turnos. Esto se debe principalmente a la gran cantidad de combinaciones y es posible que cada uno de los Nodes no se visite la cantidad suficiente de veces para comprender su resultado a largo plazo.
3. El algoritmo MCTS necesita una gran cantidad de iteraciones para poder decidir de manera efectiva la ruta más eficiente. Entonces, hay un pequeño problema de velocidad allí.