Se recomienda encarecidamente leer primero el algoritmo de Dijkstra utilizando Priority Queue .
El problema de la ruta más ancha es un problema de encontrar una ruta entre dos vértices del gráfico que maximiza el peso del borde de peso mínimo en la ruta . Vea la siguiente imagen para hacerse una idea del problema:
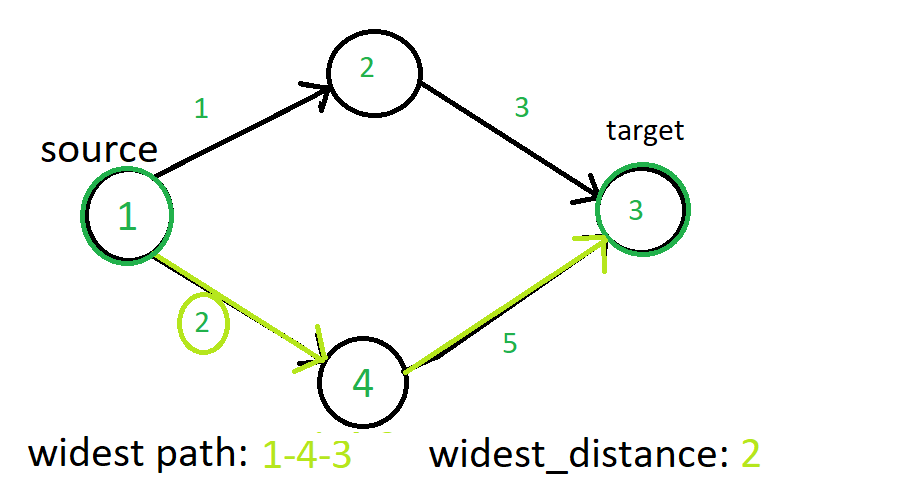
Ejemplo de aplicación práctica:
este problema es una variante famosa del algoritmo de Dijkstra. En la aplicación práctica, este problema se puede ver como un gráfico con enrutadores, ya que sus vértices y bordes representan el ancho de banda entre dos vértices. Ahora, si queremos encontrar la ruta de ancho de banda máximo entre dos lugares en la conexión a Internet, entonces este problema puede resolverse con este algoritmo.
¿Cómo resolver este problema?
Vamos a resolver este problema usando la cola de prioridad ((|E|+|V|)log|V|) implementación del algoritmo de Dijkstra con un ligero cambio.
Resolvemos este problema simplemente reemplazando la condición de relajación en el algoritmo de Dijkstra por:
max(min(distancia_mas_ancha[u], peso(u, v)), distancia_mas_ancha[v])
donde u es el vértice de origen de v. v es el vértice actual en el que estamos comprobando la condición.
Este algoritmo se ejecuta tanto para gráficos dirigidos como no dirigidos.
Vea la serie de imágenes a continuación para tener una idea sobre el problema y el algoritmo:
Los valores sobre los bordes representan los pesos de los bordes dirigidos.

Comenzaremos desde el vértice de origen y luego viajaremos por todos los vértices conectados a él y agregaremos una cola de prioridad según la condición de relajación.


Ahora aparecerá (2, 1) y 2 será el vértice de origen actual.

Ahora (3, 1) aparecerá de la cola. Pero como 3 no tiene ningún vértice conectado por la arista dirigida, no pasará nada. Entonces (4, 2) aparecerá a continuación.

Finalmente, el algoritmo se detiene, ya que no hay más elementos en la cola de prioridad.

La ruta con el valor máximo de la distancia más ancha es 1-4-3, que tiene el valor máximo de cuello de botella de 2. Así que terminamos obteniendo la distancia más ancha de 2 para alcanzar el vértice objetivo 3.
A continuación se muestra la implementación del enfoque anterior. :
CPP
// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
// Function to print the required path
void printpath(vector<int>& parent, int vertex, int target)
{
if (vertex == 0) {
return;
}
printpath(parent, parent[vertex], target);
cout << vertex << (vertex == target ? "\n" : "--");
}
// Function to return the maximum weight
// in the widest path of the given graph
int widest_path_problem(vector<vector<pair<int, int> > >& Graph,
int src, int target)
{
// To keep track of widest distance
vector<int> widest(Graph.size(), INT_MIN);
// To get the path at the end of the algorithm
vector<int> parent(Graph.size(), 0);
// Use of Minimum Priority Queue to keep track minimum
// widest distance vertex so far in the algorithm
priority_queue<pair<int, int>, vector<pair<int, int> >,
greater<pair<int, int> > >
container;
container.push(make_pair(0, src));
widest[src] = INT_MAX;
while (container.empty() == false) {
pair<int, int> temp = container.top();
int current_src = temp.second;
container.pop();
for (auto vertex : Graph[current_src]) {
// Finding the widest distance to the vertex
// using current_source vertex's widest distance
// and its widest distance so far
int distance = max(widest[vertex.second],
min(widest[current_src], vertex.first));
// Relaxation of edge and adding into Priority Queue
if (distance > widest[vertex.second]) {
// Updating bottle-neck distance
widest[vertex.second] = distance;
// To keep track of parent
parent[vertex.second] = current_src;
// Adding the relaxed edge in the priority queue
container.push(make_pair(distance, vertex.second));
}
}
}
printpath(parent, target, target);
return widest[target];
}
// Driver code
int main()
{
// Graph representation
vector<vector<pair<int, int> > > graph;
int no_vertices = 4;
graph.assign(no_vertices + 1, vector<pair<int, int> >());
// Adding edges to graph
// Resulting graph
// 1--2
// | |
// 4--3
// Note that order in pair is (distance, vertex)
graph[1].push_back(make_pair(1, 2));
graph[1].push_back(make_pair(2, 4));
graph[2].push_back(make_pair(3, 3));
graph[4].push_back(make_pair(5, 3));
cout << widest_path_problem(graph, 1, 3);
return 0;
}
Python3
# Python3 implementation of the approach # Function to print required path def printpath(parent, vertex, target): # global parent if (vertex == 0): return printpath(parent, parent[vertex], target) print(vertex ,end="\n" if (vertex == target) else "--") # Function to return the maximum weight # in the widest path of the given graph def widest_path_problem(Graph, src, target): # To keep track of widest distance widest = [-10**9]*(len(Graph)) # To get the path at the end of the algorithm parent = [0]*len(Graph) # Use of Minimum Priority Queue to keep track minimum # widest distance vertex so far in the algorithm container = [] container.append((0, src)) widest[src] = 10**9 container = sorted(container) while (len(container)>0): temp = container[-1] current_src = temp[1] del container[-1] for vertex in Graph[current_src]: # Finding the widest distance to the vertex # using current_source vertex's widest distance # and its widest distance so far distance = max(widest[vertex[1]], min(widest[current_src], vertex[0])) # Relaxation of edge and adding into Priority Queue if (distance > widest[vertex[1]]): # Updating bottle-neck distance widest[vertex[1]] = distance # To keep track of parent parent[vertex[1]] = current_src # Adding the relaxed edge in the priority queue container.append((distance, vertex[1])) container = sorted(container) printpath(parent, target, target) return widest[target] # Driver code if __name__ == '__main__': # Graph representation graph = [[] for i in range(5)] no_vertices = 4 # Adding edges to graph # Resulting graph #1--2 #| | #4--3 # Note that order in pair is (distance, vertex) graph[1].append((1, 2)) graph[1].append((2, 4)) graph[2].append((3, 3)) graph[4].append((5, 3)) print(widest_path_problem(graph, 1, 3)) # This code is contributed by mohit kumar 29
1--4--3 2
Complejidad temporal : O(E * logV), donde E es el número total de aristas y V es el número total de vértices en el gráfico.
Espacio Auxiliar : O(V).
Publicación traducida automáticamente
Artículo escrito por Aakash_Panchal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA