Mientras leemos sobre Machine Learning y Data Science, a menudo nos encontramos con un término llamado Distribución de clase desequilibrada , que generalmente ocurre cuando las observaciones en una de las clases son mucho más altas o más bajas que cualquier otra clase.
Como los algoritmos de Machine Learning tienden a aumentar la precisión al reducir el error, no consideran la distribución de clases. Este problema prevalece en ejemplos como la detección de fraude, la detección de anomalías, el reconocimiento facial, etc.
Dos métodos comunes de remuestreo son:
- Validación cruzada
- arranque
Validación cruzada –
La validación cruzada se utiliza para estimar el error de prueba asociado con un modelo para evaluar su rendimiento.
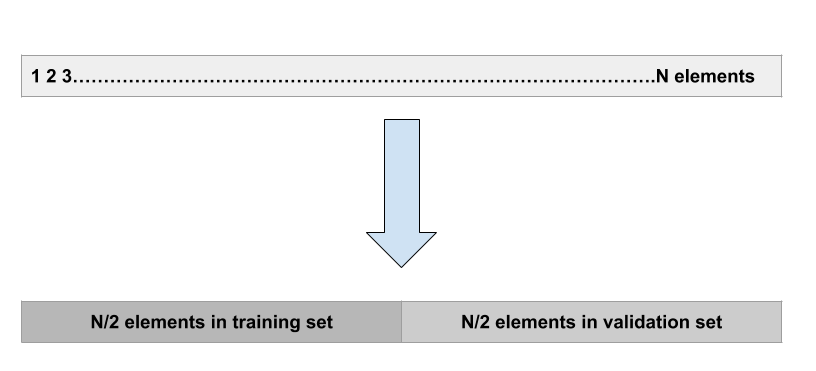
Enfoque de conjunto de validación:
Este es el enfoque más básico. Simplemente implica dividir aleatoriamente el conjunto de datos en dos partes: primero un conjunto de entrenamiento y segundo un conjunto de validación o conjunto de reserva. El modelo se ajusta al conjunto de entrenamiento y el modelo ajustado se usa para hacer predicciones en el conjunto de validación.
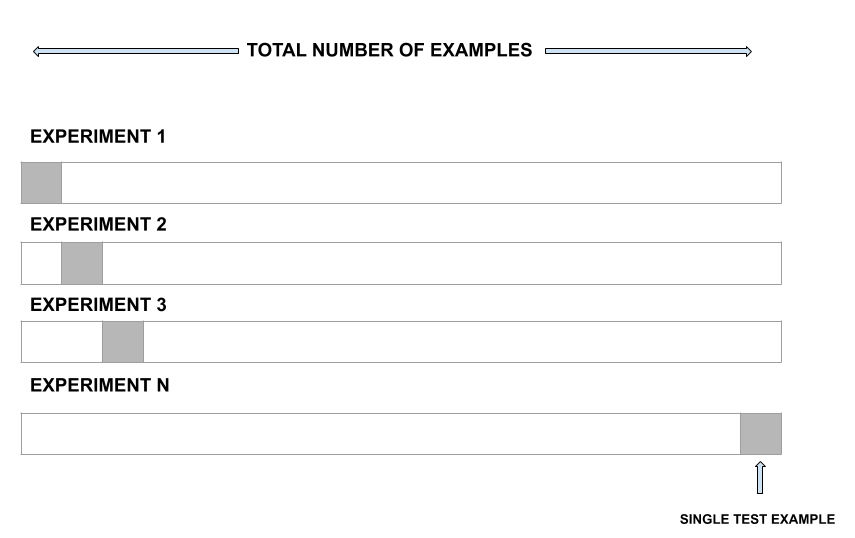
Validación cruzada de dejar uno fuera:
LOOCV es una mejor opción que el enfoque del conjunto de validación. En lugar de dividir todo el conjunto de datos en dos mitades, solo se usa una observación para la validación y el resto se usa para ajustar el modelo.
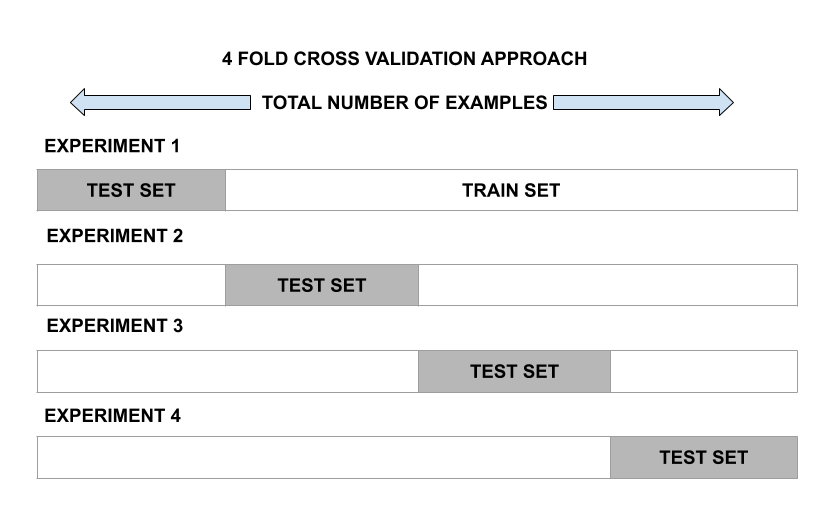
Validación cruzada de k veces:
este enfoque implica dividir aleatoriamente el conjunto de observaciones en k veces de tamaño casi igual. El primer pliegue se trata como un conjunto de validación y el modelo se ajusta en los pliegues restantes. Luego, el procedimiento se repite k veces, donde un grupo diferente cada vez se trata como el conjunto de validación.
arranque –
Bootstrap es una poderosa herramienta estadística utilizada para cuantificar la incertidumbre de un modelo dado. Sin embargo, el poder real de bootstrap es que podría aplicarse a una amplia gama de modelos donde la variabilidad es difícil de obtener o no se genera automáticamente.
Desafíos:
los algoritmos en el aprendizaje automático tienden a producir clasificadores insatisfactorios cuando se manejan con conjuntos de datos desequilibrados.
Por ejemplo, conjuntos de datos de reseñas de películas
Total Observations : 100 Positive Dataset : 90 Negative Dataset : 10 Event rate : 2%
El principal problema aquí es cómo obtener un conjunto de datos equilibrado.
Desafíos con los algoritmos de ML estándar:
las técnicas de ML estándar, como el árbol de decisión y la regresión logística, tienen un sesgo hacia la clase mayoritaria y tienden a ignorar la clase minoritaria. Tienden solo a predecir la clase mayoritaria, por lo tanto, tienen una clasificación errónea importante de la clase minoritaria en comparación con la clase mayoritaria.
La evaluación del algoritmo de clasificación se mide mediante la array de confusión.
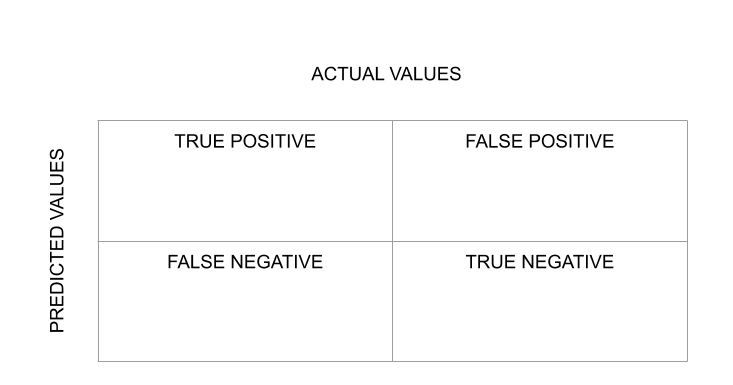
Una forma de evaluar los resultados es mediante la array de confusión, que muestra las predicciones correctas e incorrectas para cada clase. En la primera fila, la primera columna indica cuántas clases «Verdadero» se pronosticaron correctamente, y la segunda columna, cuántas clases «Verdadero» se predijeron como «Falso». En la segunda fila, observamos que todas las entradas de la clase «Falso» se predijeron como clase «Verdadero».
Por lo tanto, cuanto más altos sean los valores de la diagonal de la array de confusión, mejor será la predicción correcta.
Enfoque de manejo:
- Sobremuestreo aleatorio:
tiene como objetivo equilibrar la distribución de clases aumentando aleatoriamente los ejemplos de clases minoritarias al replicarlos.
Por ejemplo –
Total Observations : 100 Positive Dataset : 90 Negative Dataset : 10 Event Rate : 2%
- Replicamos el conjunto de datos negativos 15 veces
Positive Dataset: 90 Negative Dataset after Replicating: 150 Total Observations: 190 Event Rate : 150/240= 63%
- SMOTE (técnica de sobremuestreo de minorías sintéticas) sintetiza nuevas instancias minoritarias entre instancias minoritarias existentes. Selecciona aleatoriamente la clase minoritaria y calcula el vecino más cercano K para ese punto en particular. Finalmente, se agregan los puntos sintéticos entre los vecinos y el lugar elegido.
- Submuestreo aleatorio:
tiene como objetivo equilibrar la distribución de clases eliminando aleatoriamente los ejemplos de clases mayoritarias.
Por ejemplo –
Total Observations : 100 Positive Dataset : 90 Negative Dataset : 10 Event rate : 2% We take 10% samples of Positive Dataset and combine it with Negative Dataset. Positive Dataset after Random Under-Sampling : 10% of 90 = 9 Total observation after combining it with Negative Dataset: 10+9=19 Event Rate after Under-Sampling : 10/19 = 53%
- Cuando las instancias de dos clases diferentes están muy cerca una de la otra, eliminamos las instancias de la clase mayoritaria para aumentar los espacios entre las dos clases. Esto ayuda en el proceso de clasificación.
- Sobremuestreo basado en clústeres:
K significa que el algoritmo de agrupamiento se aplica de forma independiente tanto a las instancias de clase como para identificar clústeres en los conjuntos de datos. Todos los conglomerados se sobremuestrean de modo que los conglomerados de la misma clase tengan el mismo tamaño.
Por ejemplo –
Total Observations : 100 Positive Dataset : 90 Negative Dataset : 10 Event Rate : 2%
- Clase mayoritaria Conglomerado:
Conglomerado 1: 20 Observaciones
Conglomerado 2: 30 Observaciones
Conglomerado 3: 12 Observaciones
Conglomerado 4: 18 Observaciones
Conglomerado 5: 10 Observaciones
Clase minoritaria Conglomerado:
Conglomerado 1: 8 Observaciones
Conglomerado 2: 12 Observaciones
Después de sobremuestrear todos los conglomerados del mismo clase tienen el mismo número de observaciones.
Clase mayoritaria Conglomerado:
Conglomerado 1: 20 Observaciones
Conglomerado 2: 20 Observaciones
Conglomerado 3: 20 Observaciones
Conglomerado 4: 20 Observaciones
Conglomerado 5: 20 Observaciones
Clase minoritaria Conglomerado:
Conglomerado 1: 15 Observaciones
Conglomerado 2: 15 Observaciones
A continuación se muestra la implementación de algunas técnicas de remuestreo:
Puede descargar el conjunto de datos desde el siguiente enlace: Descarga del conjunto de datos
Python3
# importing libraries import pandas as pd import numpy as np import seaborn as sns from sklearn.preprocessing import StandardScaler from imblearn.under_sampling import RandomUnderSampler, TomekLinks from imblearn.over_sampling import RandomOverSampler, SMOTE
Python3
dataset = pd.read_csv(r'C:\Users\Abhishek\Desktop\creditcard.csv')
print("The Number of Samples in the dataset: ", len(dataset))
print('Class 0 :', round(dataset['Class'].value_counts()[0]
/len(dataset) * 100, 2), '% of the dataset')
print('Class 1(Fraud) :', round(dataset['Class'].value_counts()[1]
/len(dataset) * 100, 2), '% of the dataset')

Python3
X_data = dataset.iloc[:, :-1]
Y_data = dataset.iloc[:, -1:]
rus = RandomUnderSampler(random_state = 42)
X_res, y_res = rus.fit_resample(X_data, Y_data)
X_res = pd.DataFrame(X_res)
Y_res = pd.DataFrame(y_res)
print("After Under Sampling Of Major Class Total Samples are :", len(Y_res))
print('Class 0 :', round(Y_res[0].value_counts()[0]
/len(Y_res) * 100, 2), '% of the dataset')
print('Class 1(Fraud) :', round(Y_res[0].value_counts()[1]
/len(Y_res) * 100, 2), '% of the dataset')

Python3
tl = TomekLinks()
X_res, y_res = tl.fit_resample(X_data, Y_data)
X_res = pd.DataFrame(X_res)
Y_res = pd.DataFrame(y_res)
print("After TomekLinks Under Sampling Of Major Class Total Samples are :", len(Y_res))
print('Class 0 :', round(Y_res[0].value_counts()[0]
/len(Y_res) * 100, 2), '% of the dataset')
print('Class 1(Fraud) :', round(Y_res[0].value_counts()[1]
/len(Y_res) * 100, 2), '% of the dataset')
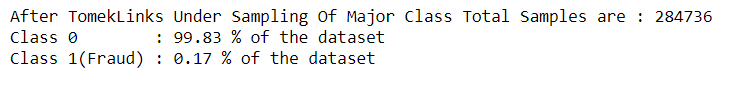
Python3
ros = RandomOverSampler(random_state = 42)
X_res, y_res = ros.fit_resample(X_data, Y_data)
X_res = pd.DataFrame(X_res)
Y_res = pd.DataFrame(y_res)
print("After Over Sampling Of Minor Class Total Samples are :", len(Y_res))
print('Class 0 :', round(Y_res[0].value_counts()[0]
/len(Y_res) * 100, 2), '% of the dataset')
print('Class 1(Fraud) :', round(Y_res[0].value_counts()[1]
/len(Y_res) * 100, 2), '% of the dataset')

Python3
sm = SMOTE(random_state = 42)
X_res, y_res = sm.fit_resample(X_data, Y_data)
X_res = pd.DataFrame(X_res)
Y_res = pd.DataFrame(y_res)
print("After SMOTE Over Sampling Of Minor Class Total Samples are :", len(Y_res))
print('Class 0 :', round(Y_res[0].value_counts()[0]
/len(Y_res) * 100, 2), '% of the dataset')
print('Class 1(Fraud) :', round(Y_res[0].value_counts()[1]
/len(Y_res) * 100, 2), '% of the dataset')

Publicación traducida automáticamente
Artículo escrito por ShauryaChauhan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA