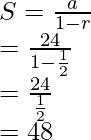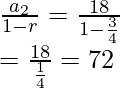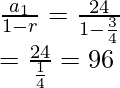Problemas verbales de secuencias y series | Clase 11 Matemáticas

Las secuencias y series tienen varias aplicaciones importantes en varias esferas de las actividades humanas. Cuando las secuencias siguen algunos patrones específicos, generalmente se les llama progresiones. Las progresiones aritméticas y geométricas son algunos ejemplos de progresiones comunes. Veamos algunos problemas sobre estas progresiones para entenderlas mejor.

Patrones de crecimiento

Estos tipos de problemas de secuencias numéricas describen primero cómo se genera una secuencia de números. Se dan algunos términos de la sucesión, y necesitamos descubrir los patrones en ellos y luego los siguientes términos de la sucesión.

Resolviendo tales secuencias:

Busca un patrón entre los números dados.
Decide si usar +, -, × o ÷
Usa el patrón para resolver la secuencia.

patrón creciente

Los patrones crecientes, como sugiere su nombre, siempre serán de naturaleza creciente. El siguiente término y el término inmediatamente anterior se relacionarán de manera similar con la ayuda de las operaciones (×, -, +).

Pregunta: 6,13,27,55, ….. En la sucesión dada, ¿cuál es el valor del siguiente término?

Responder:

Al observar detenidamente el patrón, se puede ver que

13 = 6 × 2 + 1

27 = 13 × 2 + 1

55 = 27 × 2 + 1

Esto muestra que cada término es el doble del término anterior más uno. Entonces, que el siguiente término sea «a».

a = 55 × 2 + 1

= 110 + 1

= 111

Por lo tanto, el siguiente término es 111.

Patrón decreciente

En Patrones decrecientes, el siguiente será menor que el término anterior y dos términos consecutivos seguirán un patrón determinado.

Pregunta: ¿Cuál es el siguiente término de la serie: 220,100,40, ….

Responder:

Las series siguen el patrón: 100 = (220×0.5)-10

40 = (100×0.5)-10

Por tanto, el siguiente término será (40×0.5)-10 = 10

Progresiones aritméticas

En las progresiones aritméticas, los términos consecutivos tendrán la misma diferencia y se denotan como ‘d’, el primer término se denomina ‘a’ y el número de términos se denota como ‘n’.

La fórmula para el término n ^es :

Tn = a+ ( _n -1)d

Pregunta 1: 2, 5, 8, 11, …. Encuentra el siguiente término de la sucesión.

Responder:

Se puede notar al estudiar cuidadosamente los términos de la secuencia que la diferencia entre cada término consecutivo permanece igual. Por ejemplo:

5 – 2 = 3

8 – 5 = 3

11 – 8 = 3

Entonces, el siguiente será a una diferencia de tres del último término. Como el último término de la sucesión es 11, los siguientes términos serán 14.

O

La fórmula para el término n en progresión ^aritmética también se puede usar aquí, se requiere el término 5 ^aquí :

un = 2

re = (3)

T ₅ = 2+(5-1)(3)

= 2+12

= 14

Pregunta 2: 15, 12, 9, … __. Encuentra el siguiente término.

Responder:

En este problema también, todos los términos tienen una diferencia de tres entre ellos. La diferencia es que la secuencia es de naturaleza decreciente. Como el último término es 9, el próximo término será 3 menos que el último término. Entonces, el último término será 6.

Secuencia Fibonacci

A veces hay secuencias para las que el patrón no es visible, la secuencia de Fibonacci es un ejemplo de tal secuencia. Es una secuencia muy común en el campo de las matemáticas y la informática.

El número está ordenado como, 1, 1, 2, 3, 5, 8…. Aquí el patrón no es visible, esta secuencia procede de una manera que depende de su historia.

Sea a _n el término n de la sucesión. En esta secuencia a _n = a _n-1 + a _n-2 .

Por ejemplo,

un ₂ = un ₁ + un ₀ es decir, 2 = 1 + 1,

un ₃ = un ₁ + un ₂ es decir, 3 = 2 + 1,

a ₄ = a ₃ + a ₂ es decir, 5 = 2 + 3 y,

un ₅ = un ₄ + un ₃ es decir, 8 = 5 + 3.

Pregunta: ¿Cuál es el siguiente término en la serie de Fibonacci: 1,1,2,3,5,8,13,……

Responder:

En la serie de Fibonacci, el siguiente término es la suma de los dos últimos términos.

Por tanto, el siguiente término será (8+13)= 21

Series geométricas

Antes de empezar con los problemas relacionados con una progresión geométrica. Hagamos un resumen rápido de las fórmulas para la suma y el enésimo término de un GP.

La forma general de una progresión geométrica es a, ar, ar ² , ar ³ …… donde a = primer término, r = razón común y a ⁿ el enésimo término.

El enésimo término de la progresión: a ⁿ = ar ^n-1 .
Suma de n-términos de GP: $S_{n} = a[\frac{r^{n}-1}{r-1}] \text{ where } r \ne 1$
Suma de GP infinitos: $S_{n} = \frac{a}{1-r}$

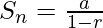
Problemas de GP finitos

Este tipo de problemas incluyen las series geométricas donde hay un número finito de términos.

Pregunta 1: El número de bacterias en un determinado cultivo se duplica cada hora. Si originalmente había 30 bacterias presentes en el cultivo, ¿cuántas bacterias estarán presentes al final de la segunda hora, la cuarta hora y la enésima hora?

Responder:

El crecimiento de la bacteria hace un GP, 30, 60, 120,….. y así sucesivamente.

En este PG, a = 30, r = 2. Sea a n el número de bacterias en la hora _n .

En n = 2, a ² = ar ^2-1

= (30)(2) ^2-1 = 30 × 2 = 60

En n = 4, a ⁴ = ar ^4-1

= (30)(2) ^4-1 = 30 × 2 ³ = 240

En el paso n an = ar ^(n-1) = 30 × 2 ^n-1

Pregunta 2: Una persona tiene 2 padres, 4 abuelos, 8 bisabuelos, etc. Encuentre el número de sus antepasados durante las diez generaciones anteriores a la suya.

Responder:

Este es un problema de GP finito. La secuencia se puede pensar así,

2, 4, 8, 16, …..

Entonces, el número total de antepasados en 10 generación de su familia.

2, 4, 8, 16, 32, …..10 términos.

Aquí, a = 2, r = 2 y n = 10

S10 = un $S_{n} = a[\frac{r^{n}-1}{r-1}] \\ = 2[\frac{2^{10} - 1}{2 - 1}] \\ = 2[1023] = 2046$

Problemas infinitos de GP

Una serie geométrica infinita es la suma de una secuencia geométrica infinita. Esta serie no tendría un último término.

$S_\infty = \sum_{n=1}^{\infty}ar^{n-1} = \frac{a}{1-r}; -1<{r}<1$

Pregunta 1: Un mono se balancea de un árbol. En el primer giro, atraviesa un arco de 24 m. Con cada golpe, atraviesa un arco de 24 m. Con cada golpe, pasa a través de un arco de la mitad de la longitud del golpe anterior. ¿Cuál es la distancia total recorrida por el mono cuando completa su swing número 100000?

Responder:

Ahora este movimiento representa un GP con a = 24 y r = 1/2. Ahora, dado que el GP está disminuyendo y la pregunta pide la suma hasta el término 100000. Para ahorrarnos el cálculo, podemos considerarlo un GP infinito y redondear la respuesta que obtengamos.

Suma de un GP infinito = $\frac{a}{1-r}$

Aquí, a = 24 y r = 1/2. Sea la suma S

$S = \frac{a}{1-r} \\ = \frac{24}{1-\frac{1}{2}} \\ = \frac{24}{\frac{1}{2}}\\ = 48$

Así que el mono viaja casi 24 m en todos estos columpios.

Pregunta 2: Se dejó caer una pelota desde una mesa de 24 pulgadas de alto. La pelota rebota y siempre llega a las tres cuartas partes de la distancia caída. ¿Cuál es la distancia aproximada que recorre la pelota antes de finalmente detenerse en el suelo?

Responder:

Debe notarse que este problema en realidad involucra dos series geométricas infinitas. La primera serie involucra la caída de la pelota y la otra serie involucra la elevación de la pelota después de rebotar en el suelo.

Cayendo: a ₁ = 24 , r = 3/4

Ascendente: a ₂ = 24(3/4) = 18 ,r = 3/4

Usando la fórmula para series geométricas infinitas,

S = $\frac{a}{1-r}$

Sea S la distancia total recorrida:

S = S _ascendente + S _descendente

S _ascendente = $\frac{a_{2}}{1 - r} = \frac{18}{1 - \frac{3}{4}} \\ = \frac{18}{\frac{1}{4}} = 72$

S _cayendo = $\frac{a_{1}}{1-r} = \frac{24}{1 - \frac{3}{4}} \\ = \frac{24}{\frac{1}{4}} = 96$

Ahora, S = S _ascendente + S _descendente = 72 + 96 = 168

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Patrones de crecimiento

patrón creciente

Patrón decreciente

Progresiones aritméticas

Secuencia Fibonacci

Series geométricas

Problemas de GP finitos

Problemas infinitos de GP

Deja una respuesta Cancelar la respuesta