El valor aritmético que se usa para representar la cantidad y se usa para hacer cálculos se define como Números. Un símbolo como «4,5,6» que representa un número se conoce como números. Sin números, no podemos contar cosas, fecha, hora, dinero, etc. Estos números también se usan para medir y etiquetar.
Las propiedades de los números los hacen útiles para realizar operaciones aritméticas con ellos. Estos números se pueden escribir en formas numéricas y también en palabras.
Por ejemplo, 3 se escribe como tres en palabras, 35 se escribe como treinta y cinco en palabras, etc. Los estudiantes pueden escribir los números del 1 al 100 en palabras para aprender más.
Hay diferentes tipos de números, que podemos aprender. Son números enteros y naturales, números pares e impares, números racionales e irracionales, etc.
¿Qué es el sistema numérico?
Un Sistema Numérico es un método de mostrar números por escrito, que es una forma matemática de representar los números de un conjunto dado, usando los números o símbolos de manera matemática. El sistema de escritura para denotar números usando dígitos o símbolos de manera lógica se define como Sistema Numérico.
Podemos usar los dígitos del 0 al 9 para formar todos los números. Con estos dígitos, cualquiera puede crear números infinitos.
Por ejemplo, 156,3907, 3456, 1298, 784859, etc.
¿Qué es una raíz cuadrada?
El valor del número de raíces cuadradas, que al multiplicarse por sí mismo da el número original. Supongamos que a es la raíz cuadrada de b, entonces se representa como a=√b o podemos expresar la misma ecuación como a 2 = b. Aquí, ‘√’ este símbolo que usamos para representar la raíz de los números se denomina radical. El número positivo cuando se va a multiplicar por sí mismo representa el cuadrado del número. La raíz cuadrada del cuadrado de cualquier número positivo da el número original.
Por ejemplo, el cuadrado de 4 es 16, 4 2 = 16, y la raíz cuadrada de 16, √16 = 4. Dado que 4 es un cuadrado perfecto, es fácil encontrar la raíz cuadrada de tales números, pero para un cuadrado imperfecto, es muy complicado.
La raíz cuadrada se representa como ‘√’. Se llama un símbolo radical. Para representar un número ‘a’ como raíz cuadrada usando este símbolo se puede escribir como ‘√a’, donde a es el número.
El número aquí debajo del símbolo radical se llama radicando. Por ejemplo, la raíz cuadrada de 4 también se representa como un radical de 4. Ambos representan el mismo valor.
y La fórmula para encontrar la raíz cuadrada es: b = √a
Propiedades de la raíz cuadrada
Se define como una función uno a uno que toma un número positivo como entrada y devuelve la raíz cuadrada del número de entrada dado.
f(x) = √x
Por ejemplo, aquí si x = 9, entonces la función devuelve el valor de salida como 3.
Estas propiedades de la raíz cuadrada son las siguientes:
- Si un número es un número cuadrado perfecto, definitivamente existe una raíz cuadrada perfecta.
- Si un número termina con un número par de ceros (0), entonces podemos tener una raíz cuadrada.
- Los dos valores de la raíz cuadrada se pueden multiplicar. Por ejemplo, √3 se puede multiplicar por √2, entonces el resultado será √6.
- Cuando se multiplican dos raíces cuadradas iguales, el resultado debe ser un número radical. Muestra que el resultado es un número que no es raíz cuadrada. Por ejemplo, cuando √7 se multiplica por √7, el resultado obtenido es 7.
- La raíz cuadrada de los números negativos no está definida. por lo tanto, el cuadrado perfecto no puede ser negativo.
- Parte de un número termina en 2, 3, 7 u 8 (en el dígito de la unidad), entonces la raíz cuadrada perfecta no existe.
- Parte de un número termina con 1, 4, 5, 6 o 9 en el dígito de la unidad, entonces el número tendrá una raíz cuadrada.
Métodos para encontrar la raíz cuadrada
Es fácil encontrar la raíz cuadrada de un número que es un cuadrado perfecto.
Los cuadrados perfectos son aquellos números positivos que se pueden escribir como la multiplicación de un número por sí mismo. o puedes decir que los cuadrados perfectos son números que es el valor de la potencia 2 de cualquier número entero.
Podemos usar cuatro métodos para encontrar la raíz cuadrada de los números y estos métodos son los siguientes:
- Método de resta repetida de la raíz cuadrada
- Método de raíz cuadrada por factorización prima
- Raíz cuadrada por método de estimación
- Método de raíz cuadrada por división larga
Los tres métodos anteriores se pueden usar convenientemente para cuadrados perfectos, mientras que el cuarto método, es decir, el método de división larga, se puede usar para todos los números, ya sea un cuadrado perfecto o no.
Método de resta repetida de la raíz cuadrada
Es un método muy simple, aquí restaremos los números impares consecutivos del número para el cual estamos encontrando la raíz cuadrada hasta llegar a 0. En este método, el número de veces que restamos es la raíz cuadrada del número dado. Este método solo funciona para números cuadrados perfectos. Encontremos la raíz cuadrada de 25 usando este método.
Ejemplo:
25 – 1 = 24
24 – 3 = 21
21 – 5 = 16
16 – 7 = 9
9 – 9 = 0
Aquí hemos restado 5 veces por lo que la raíz cuadrada perfecta de 25 es 5
Método de raíz cuadrada por factorización prima
La descomposición en factores primos de cualquier número significa representar ese número en particular como un producto de números primos. Para encontrar la raíz cuadrada de un número dado a través del método de descomposición en factores primos, se deben seguir algunos pasos:
Paso 1: Aquí dividiremos el número dado en sus factores primos.
Paso 2: Forme pares de factores similares de modo que ambos factores en cada par sean iguales.
Paso 3: Toma un factor del par.
Paso 4: Encuentra el producto de los factores obtenidos al tomar un factor de cada par.
Paso 5: Ese producto es la raíz cuadrada del número dado.
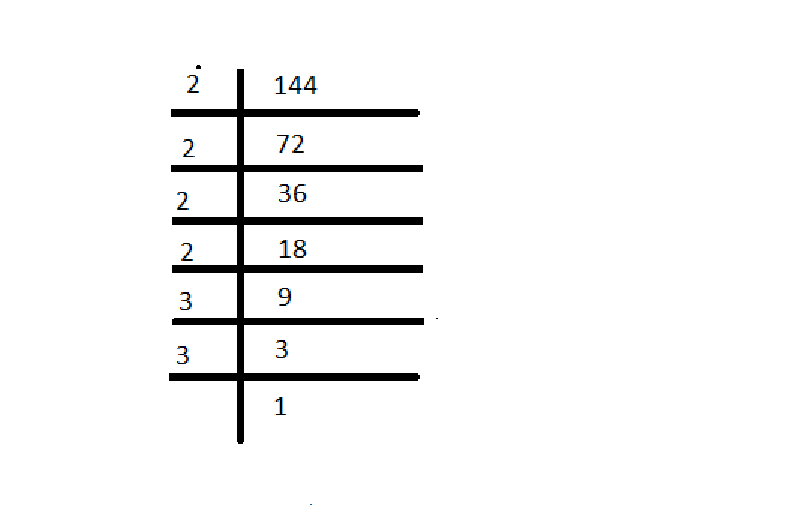
Ejemplo: Encuentra la raíz cuadrada de 144 por este método
Entonces, la raíz cuadrada de 144 es 2 × 2 × 2 × 2 × 3 × 3
= 2 2 × 2 2 × 3 2
podemos escribir como = (2 × 2 × 3) 2
= (12) 2
Raíz cuadrada perfecta de 225

Aquí la raíz cuadrada de 225 es
Podemos escribir como 5 × 5 × 3 × 3
= 5 2 × 3 2
= (5 × 3) 2
= (15) 2
Raíz cuadrada por método de estimación
La estimación y la aproximación se refieren a una suposición razonable del valor real para facilitar los cálculos. Este método también ayuda a estimar y aproximar la raíz cuadrada de un número dado.
Usemos este método para encontrar √15 y encontrar los números cuadrados perfectos más cercanos a 15 .
Sabemos que 9 y 16 son los números cuadrados perfectos más cercanos a 15. También sabemos que √16 = 4 y √9 = 3.
Esto también implica que √15 se encuentra entre 3 y 4 . Ahora, necesitamos ver si √15 está más cerca de 3 o de 4.
Consideremos 3.5 y 4.
3.5 2 = 12.25 y 4 2 = 16. Por lo tanto, √15 se encuentra entre 3.5 y 4 y más cerca de 4.
Ahora, encontraremos los cuadrados de 3.8 y 3.9.
3,8 2 = 14,44 y 3,9 2 = 15,21.
Esto también implica que √15 se encuentra entre 3,8 y 3,9. Repetimos el proceso y comprobamos entre 3,85 y 3,9.
Entonces podemos observar que √15 = 3.872.
Este es un proceso que consume mucho tiempo.
Método de raíz cuadrada por división larga
Es un método para dividir números grandes en pasos o partes, dividiendo el problema de división en una secuencia de pasos más fáciles. Con este método, podemos encontrar la raíz cuadrada exacta de cualquier número dado.
Primero, tenemos que emparejar el número en dos partes, para los dígitos antes del número decimal, emparejamos desde la derecha, mientras que para los números después del decimal, emparejamos desde la derecha del decimal.
Así que ahora aquí algunos ejemplos de la raíz cuadrada de 20.8849 y nos da una raíz cuadrada perfecta.
Encuentra la raíz cuadrada correcta hasta 2 decimales 60.92
Usando el método de división larga
Pasos que hemos usado aquí para calcular:
1) Primero tenemos que emparejar el número 60.92 en dos partes
para los dígitos antes del número decimal, emparejamos desde la derecha
mientras que para los números después del decimal emparejamos desde la derecha del decimal….
Entonces la raíz cuadrada de 60.92 es 7.805126 no tiene una raíz cuadrada perfecta….
Usando el método de resta repetida
Solución:
60,92 – 1 = 59,92
59,92 – 3 = 56,92
56,92 – 5 = 51,92
51,92 – 7 = 44,92
44,92 – 9 = 35,92
35,92 – 11= 24,92
24,92 – 13 = 11,92
11,92 – 15 = – 4,92
A partir de aquí, muestra que con este método no obtendremos el 0 después de continuar con la resta, ya que el resultado ahora es menos … por lo que muestra que 60.92 no tiene una raíz cuadrada perfecta … por lo tanto, este método no es exitoso o puede decir solo exitoso para los números que tienen raíz cuadrada perfecta…
Publicación traducida automáticamente
Artículo escrito por adnanirshad158 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA