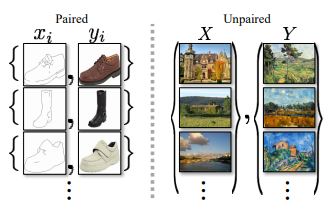
Cycle Generative Adversarial Network (CycleGAN)

Las GAN fueron propuestas por Ian Goodfellow. Cycle GAN se utiliza para transferir características de una imagen a otra o puede mapear la distribución de imágenes a otra. En CycleGAN tratamos el problema como un problema de reconstrucción de imágenes. Primero tomamos una entrada de imagen (x) y usamos el generador G para convertirla en la imagen reconstruida. Luego invertimos este proceso de imagen reconstruida a imagen original usando un generador F. Luego calculamos la pérdida de error cuadrático medio entre la imagen real y la reconstruida. La característica más importante de este ciclo_GAN es que puede hacer esta traducción de imagen en una imagen no emparejada donde no existe relación entre la imagen de entrada y la imagen de salida.

Arquitectura

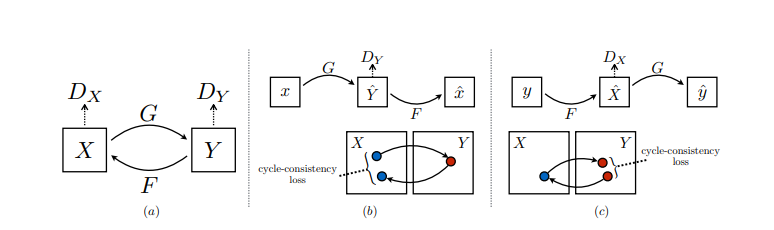
Al igual que toda la red antagónica, CycleGAN también tiene dos partes, Generador y Discriminador, el trabajo del generador para producir las muestras de la distribución deseada y el trabajo del discriminador es averiguar si la muestra es de la distribución real (real) o de la que son generado por generador (falso).

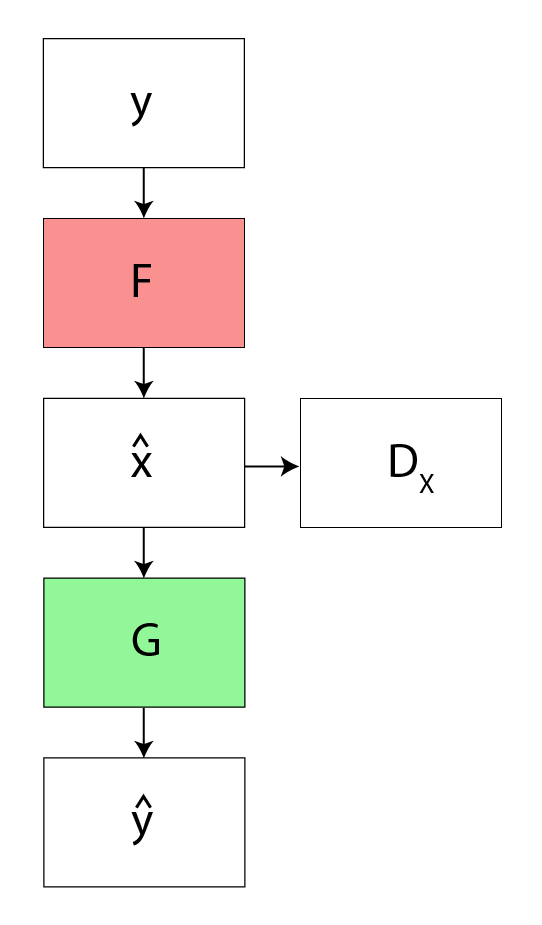
La arquitectura CycleGAN se diferencia de otras GAN en que contiene 2 funciones de mapeo ( G y F ) que actúan como generadores y sus correspondientes Discriminadores (Dx y Dy): Las funciones de mapeo del generador son las siguientes:

$\begin{array}{l} G : X \rightarrow Y \\ F : Y \rightarrow X \end{array}$

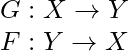
donde X es la distribución de la imagen de entrada e Y es la distribución de salida deseada (como los estilos de Van Gogh). Los discriminadores correspondientes a estos son:

Dx: distingue G (X) (salida generada) de Y (salida real)

Dy: distingue F(Y)(Salida inversa generada) de X (Distribución de entrada)

Para regularizar aún más las asignaciones, los autores usaron dos funciones de pérdida más además de la pérdida contradictoria. La pérdida de consistencia del ciclo hacia adelante y la pérdida de consistencia del ciclo hacia atrás. La pérdida de consistencia del ciclo directo refina el ciclo:

$x --> G(x) -->F(G(x)) \approx x$

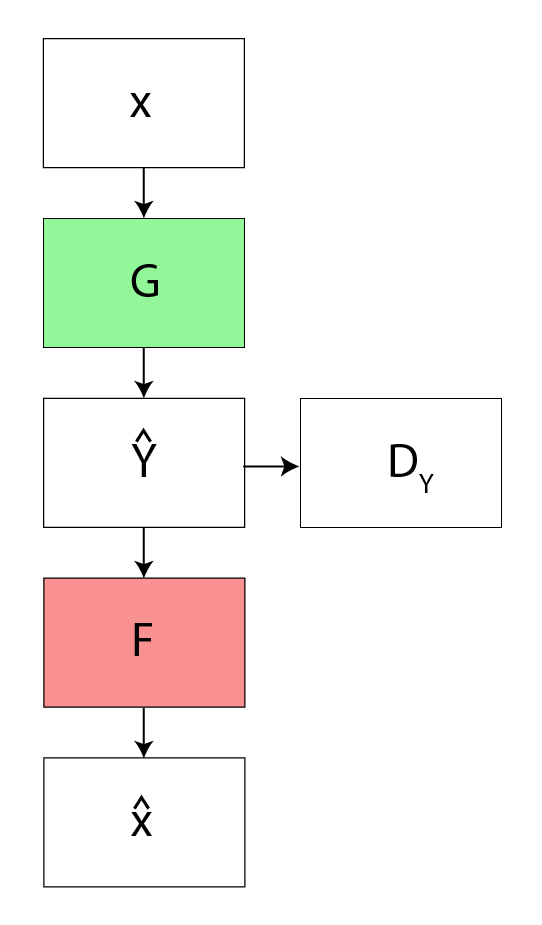
La pérdida de consistencia del ciclo hacia atrás refina el ciclo:

$y--> F(y) -->G(F(y)) \approx y$

Arquitectura del generador:

Cada generador CycleGAN tiene tres secciones:

codificador
Transformador
Descifrador

La imagen de entrada se pasa al codificador. El codificador extrae características de la imagen de entrada mediante el uso de circunvoluciones y comprime la representación de la imagen, pero aumenta el número de canales. El codificador consta de 3 convoluciones que reducen la representación en 1/4 del tamaño real de la imagen. Considere una imagen de tamaño (256, 256, 3) que ingresamos en el codificador, la salida del codificador será (64, 64, 256).

Luego, la salida del codificador después de aplicar la función de activación se pasa al transformador. El transformador contiene 6 o 9 bloques residuales según el tamaño de la entrada. La salida del transformador luego se pasa al decodificador que utiliza un bloque de deconvolución de 2 pasos de fracción para aumentar el tamaño de la representación al tamaño original.

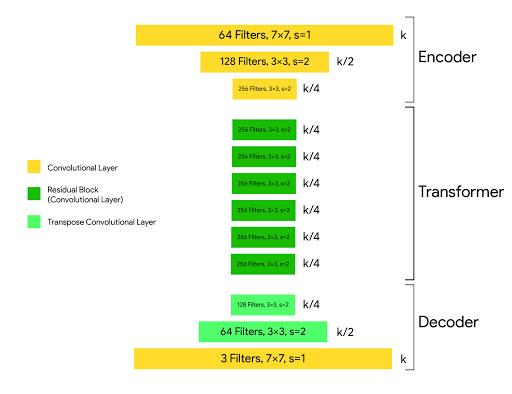
La arquitectura del generador es:

c7s1-64, d128, d256, R256, R256, R256,

R256, R256, R256, u128, u64, c7s1-3

donde c7s1-k denota una capa Convolution-InstanceNorm-ReLU de 7×7 con k filtros y zancada 1. dk denota una capa Convolution-InstanceNorm-ReLU de 3 × 3 con k filtros y zancada 2. Rk denota un bloque residual que contiene dos 3 × 3 capas de convolución con el mismo número de filtros en ambas capas. uk denota una capa de 3 × 3 fraccionales-zancadas-Convolución-InstanciaNorma-ReLU con k filtros y zancada 1/2 (es decir, operación de deconvolución).

Arquitectura discriminadora:

En el discriminador los autores usan el discriminador PatchGAN. La diferencia entre un PatchGAN y un discriminador GAN normal es que, más bien, el GAN normal mapea desde una imagen de 256 × 256 a una única salida escalar, lo que significa «real» o «falso», mientras que PatchGAN mapea desde 256 × 256 a un NxN ( aquí 70 × 70) array de salidas X, donde cada X _ij significa si el parche ij en la imagen es real o falso.

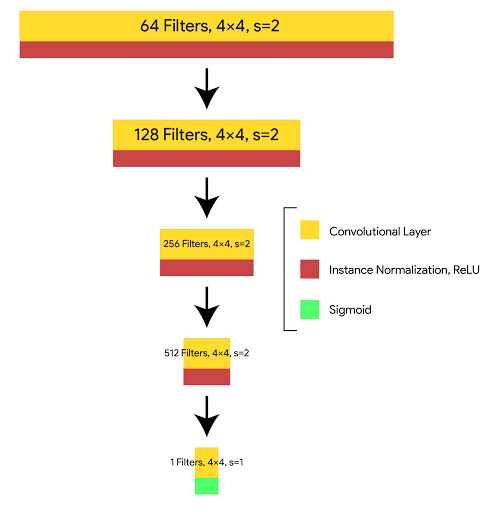
La arquitectura del discriminador es:

C64-C128-C256-C512

donde Ck es una capa de convolución-InstanceNorm-LeakyReLU de 4 × 4 con k filtros y zancada 2. No aplicamos InstanceNorm en la primera capa (C64). Después de la última capa, aplicamos la operación de convolución para producir una salida de 1×1.

Función de costo:

Pérdida por adversario: aplicamos la pérdida por adversario a nuestros mapeos de generadores y discriminadores. Esta pérdida del adversario se escribe como:

$Loss_{advers}\left ( G, D_y, X, Y \right ) =\frac{1}{m}\sum \left ( 1 - D_y\left ( G\left ( x \right ) \right ) \right )^{2} \,$
$Loss_{advers}\left ( F, D_x, Y, X \right ) =\frac{1}{m}\sum \left ( 1 - D_x\left ( F\left ( y \right ) \right ) \right )^{2}$

Pérdida de consistencia del ciclo : dado un conjunto aleatorio de imágenes, la red antagónica puede asignar el conjunto de imágenes de entrada a una permutación aleatoria de imágenes en el dominio de salida, lo que puede inducir una distribución de salida similar a la distribución de destino. Por lo tanto, el mapeo contradictorio no puede garantizar la entrada x _i a y _i . Para que esto suceda, el autor propuso que el proceso debe ser coherente con el ciclo. Esta función de pérdida se usa en Cycle GAN para medir la tasa de error del mapeo inverso G(x) -> F(G(x)). El comportamiento inducido por esta función de pérdida hace que coincida estrechamente la entrada real (x) y F(G(x))

$Loss_{cyc}\left ( G, F, X, Y \right ) =\frac{1}{m}\left [ \left ( F\left ( G\left ( x_i \right ) \right )-x_i \right ) +\left ( G\left ( F\left ( y_i \right ) \right )-y_i \right ) \right ]$

La función de costo que usamos es la suma de la pérdida contradictoria y la pérdida constante cíclica:

$L\left ( G, F, D_x, D_y \right ) = L_{advers}\left (G, D_y, X, Y \right ) + L_{advers}\left (F, D_x, Y, X \right ) + \lambda L_{cycl}\left ( G, F, X, Y \right )$

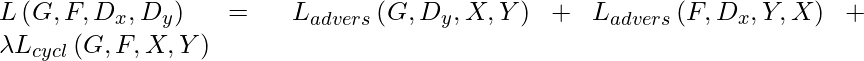
y nuestro objetivo es:

$arg \underset{G, F}{min}\underset{D_x, D_y}{max}L\left ( G, F, D_x, D_y \right )$

Aplicaciones:

Transferencia de estilo de colección: los autores entrenaron al modelo con fotografías de paisajes descargadas de Flickr y WikiArt. A diferencia de otros trabajos sobre la transferencia de estilo neuronal, CycleGAN aprende a imitar el estilo de una colección completa de obras de arte, en lugar de transferir el estilo de una sola obra de arte seleccionada. Por lo tanto puede generar diferentes estilos como: Van Gogh, Cezanne, Monet y Ukiyo-e.

Resultados de transferencia de estilo

Comparación de diferentes resultados de transferencia de estilo

Transformación de objetos : CycleGAN puede transformar objetos de una clase de ImageNet a otra, como: cebra a caballos y viceversa, manzanas a naranjas y viceversa, etc.
- Manzana <—> Naranjas:

Transferencia de temporada : CycleGAN también puede transferir imágenes de la temporada de invierno a la temporada de verano y viceversa. Para ello, la modelo se entrena con 854 fotos de invierno y 1273 fotos de verano de Yosemite de Flickr.

Generación de fotografías a partir de pinturas : CycleGAN también se puede utilizar para transformar fotografías a partir de pinturas y viceversa. Sin embargo, para mejorar esta transformación, los autores también introdujeron una pérdida adicional llamada Pérdida de identidad. Esta pérdida se puede definir como:

$L_{identity}\left ( G, F \right ) =\mathbb{E}_{y~p\left ( y \right )}\left [ \left \| G(y)-y \right \|_1 \right ] + \mathbb{E}_{x~p\left ( x \right )}\left [ \left \| F(x)-x \right \|_1 \right ]$

Mejora de fotografías : CycleGAN también se puede utilizar para mejorar fotografías. Para esto, el modelo toma imágenes de dos categorías que se capturan desde la cámara del teléfono inteligente (generalmente tienen una profundidad de campo profunda debido a la baja apertura) a DSLR (que tienen una profundidad de campo más baja). Para esta tarea, el modelo transforma imágenes de teléfonos inteligentes a imágenes de calidad DSLR.

Métricas de evaluación:

Estudios perceptuales de AMT: para la tarea de fotografía aérea del mapa, los autores realizan estudios perceptivos «reales frente a falsos» en Amazon Mechanical Turk (AMT) para evaluar el realismo de nuestros resultados. . A los participantes se les mostró una secuencia de pares de imágenes, una foto o mapa real y otra falsa (generada por nuestro algoritmo o una línea de base), y se les pidió que hicieran clic en la imagen que creían que era real.
Puntuaciones FCN: Para el conjunto de datos fotográficos de Cityscapeslabels, la puntuación FCN de los autores. El FCN predice un mapa de etiquetas para una foto generada. Este mapa de etiquetas se puede comparar con las etiquetas de verdad de campo de entrada utilizando métricas de segmentación semántica estándar. Aquí las métricas de segmentación estándar que se utilizan en el conjunto de datos de Cityscapes, como la precisión por píxel, por IoU de clase y IoU de clase media.

Resultados:

Para la tarea aérea del mapa, los resultados de la prueba AMT «real vs fake» son los siguientes:

En esta tarea, los autores extrajeron datos de Google Maps y Google Earth y los evaluaron en diferentes métodos GAN y los compararon con Ground Truth.

Rendimiento de clasificación para diferentes métricas

Algunos de los resultados del conjunto de datos de Cityscapes son los siguientes

Inconvenientes y limitaciones:

CycleGAN puede ser útil cuando necesitamos realizar una transformación de color o textura, sin embargo, cuando se aplica para realizar una transformación geométrica, CycleGAN no funciona muy bien. Esto se debe a la arquitectura del generador que está entrenada para realizar cambios de apariencia en la imagen.

Casos de Falla del Ciclo GAN

Referencias:

Traducción de imagen a imagen no emparejada utilizando redes antagónicas coherentes con el ciclo

Publicación traducida automáticamente

Artículo escrito por pawangfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta