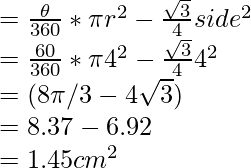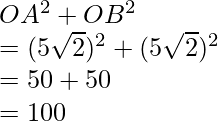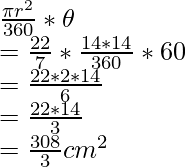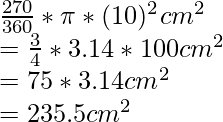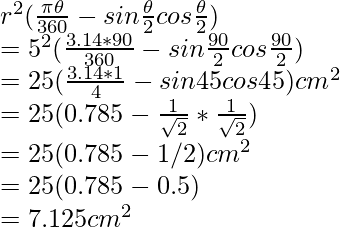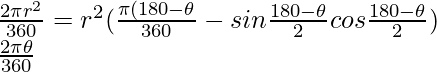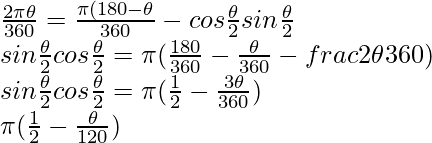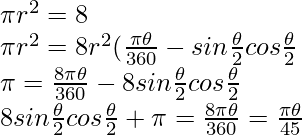Clase 10 RD Sharma- Capítulo 15 Áreas relacionadas con círculos – Ejercicio 15.3

Pregunta 1. AB es una cuerda de un círculo con centro O y radio 4 cm. AB tiene una longitud de 4 cm y divide el círculo en dos segmentos. Encuentra el área del segmento menor.

Solución:

Dado,

Radio de la circunferencia de centro O, dado por OA y OB = r = 4 cm

Además, la longitud de la cuerda dada AB = 4 cm

Como todos los lados son iguales, OAB es un triángulo equilátero donde el ángulo AOB = 60°

Así, el ángulo subtendido en el centro θ es igual a 60°

Ahora,

Área del segmento menor = (Área del sector) – (Área del triángulo AOB)

$= \frac{\theta}{360} * \pi r^2 - \frac{\sqrt3}{4}side^2 \\ = \frac{60}{360} * \pi4^2 - \frac{\sqrt3}{4}4^2 \\ = (8\pi /3 - 4\sqrt3) \\ = 8.37 - 6.92 \\ = 1.45 cm^2$

Por lo tanto, ahora el área requerida del segmento está dada por (8π/3 – 4√3) cm ²

Pregunta 2. Una cuerda PQ de 12 cm de longitud subtiende un ángulo de 120o en el centro de un círculo. Encuentre el área del segmento menor cortado por la cuerda PQ.

Solución:

Tenemos, ∠POQ = 120 ^o y el segmento de recta PQ = 12 cm

Dibuja el segmento de línea OV ⊥ PQ,

Ahora,

VP = PQ × (0,5) = 12 × 0,5 = 6 cm

Como, ∠POV = 120 ^o

También,

∠POV = ∠QOV = 60 ^o

Tenemos,

En el triángulo OPQ tenemos

Sin θ = PV/ OA

Sen 60 ^o = 6/ OA

Sustituyendo los valores, obtenemos,

√3/2 = 6/ OA

AO = 12/ √3 = 4√3 = r

Ahora, calculando el área del segmento menor

Área del segmento = área del sector OPUQO – área de △OPQ

= θ/360 x πr2 – ½ x PQ x OV

= 120/360 x π(4√3)2 – ½ x 12 x 2√3

= 16π – 12√3 = 4(4π – 3√3)

Por eso,

Área del segmento menor = 4(4π – 3√3) cm2

Pregunta 3. Una cuerda de un círculo de 14 cm de radio forma un ángulo recto en el centro. Encuentra las áreas de los segmentos mayor y menor del círculo.

Solución:

Dado,

El radio (r) del círculo está dado por = 14 cm

Ángulo subtendido por la cuerda con el centro del círculo, θ está dado por 90°

Ahora,

Área del segmento menor = θ/360 x πr ² – ½ xr ² sen θ

Sustituyendo los valores, obtenemos,

= 90/360 x π(14) ² – ½ x 14 ² sen (90°)

= ¼ x (22/7) (14) ² – 7 × 14

⁼ 56cm2

Área del círculo = πr ²

Sustituyendo los valores,

= 22/7 x (14) ² = 616 cm ²

Así, sabemos,

El área del segmento mayor = Área del círculo – Área del segmento menor

= 616 – 56 = 560 ^cm2

Pregunta 4. Se dibuja una cuerda de 10 cm de largo en un círculo cuyo radio es de 5√2 cm. Encuentra el área de ambos segmentos.

Solución:

Dado,

Radio del círculo, r = 5√2 cm = OA = OB

Longitud de la cuerda AB = 10 cm

Ahora,

En el triángulo OAB,

$OA^2 + OB^2 \\ = (5\sqrt2)^2+ (5\sqrt2)^2 \\ = 50 + 50 \\ = 100$

AB2 ⁼ 100

Por lo tanto, se cumple el teorema de Pitágoras, es decir, OAB es un triángulo rectángulo.

Ángulo subtendido por la cuerda en el centro del círculo, θ = 90°

Sabemos,

Área del segmento menor = área del sector – área del triángulo

Sustituyendo los valores,

= θ/360 × πr ² – ½ xr ² sen θ

= 90/360 × (3,14) 5√2 ² – ½ x (5√2) ² sen 90

= [¼ x 3,14 x 25 x 2] – [½ x 25 x 2 x 1]

Obtenemos,

= 25(1.57 – 1)

= 14,25 cm2

Área del círculo = πr ² = 3,14 x (5√2) ² = 3,14 x 50 = 157 cm ²

De este modo,

Área del segmento mayor = Área del círculo – Área del segmento menor

= 157 – 14,25

= 142,75 ^cm2

Pregunta 5. Una cuerda AB de un círculo de 14 cm de radio forma un ángulo de 60° en el centro de un círculo. Encuentra el área del segmento menor del círculo.

Solución:

Dado,

El radio del circulo (r) esta dado por= 14 cm = OA = OB

Ángulo subtendido por la cuerda en el centro del círculo, θ = 60°

En el triángulo AOB, dado que los ángulos opuestos a los lados iguales son iguales,

Por lo tanto, ángulo A = ángulo B

Por la propiedad de la suma de los ángulos,

∠A + ∠B + ∠O = 180

x + x + 60° = 180°

2x = 120°, x = 60°

Como todos los ángulos miden 60° cada uno, el triángulo OAB es un equilátero con OA = OB = AB

Sabemos,

Área del segmento menor = área del sector – área del triángulo OAB

= θ/360 × πr ² – 1/2 r ² sen θ

= θ/360 × πr ² – 1/2 x (14) ² sen 60°

= 60/360 × (22/7) 142 – 1/2 × (14) ² × √3/2

= 60/360 x (22/7) 142 – √3/4 x (14) ²

= 142 [(1/6) x (22/7)] – 0,4330

= 142 [(22/42)] – 0,4330

= 142 [(11-9.093)/21]

= 142 [0,09080]

= 17,79

Por tanto, el área del segmento menor = 17,79 cm ²

Pregunta 6. Halla el área del segmento menor de un círculo de radio 14 cm, cuando el ángulo del sector correspondiente es de 60°. [Ejemplo Ncert]

Solución:

Tenemos,

Radio del círculo, r = 14 cm

Angulo central del sector correspondiente = 60 ^°

Como OA = OB = r, entonces, el triángulo AOB es un triángulo isósceles.

∠OAB = ∠OBA = θ

Ahora, en el triángulo OAB, por la propiedad de la suma de ángulos

∠AOB + ∠OAB + ∠OBA = 180°

Sustituyendo valores,

60° + θ + θ = 180°

resolver,

θ = 60°

Ahora bien, como todos los ángulos son iguales, entonces es un triángulo equilátero, con lados iguales, es decir,

OA = OB = AB = 14 cm

Área del triángulo OAB = $\sqrt3/4 * (14)^2$

Sustituyendo los valores, obtenemos

Área = 49 √3 cm ²

También,

Área del sector OBAO = $\frac{\pi r^2}{360 \degree} * \theta \\ = \frac{22}{7} * \frac{14*14}{360} * 60\degree \\ = \frac{22 * 2 * 14}{6} \\ = \frac{22 * 14}{3} \\ = \frac{308}{3} cm^2$

Ahora,

Área del segmento menor = Área del sector OBAO – Área del triángulo OAB = $\frac{308}{3} - 49\sqrt3 cm^2$

Pregunta 7. Una cuerda de un círculo de 20 cm de radio subtiende un ángulo de 90° en el centro. Encuentre el área del segmento mayor correspondiente del círculo. (Use π = 3.14) [Ncert Ejemplar]

Solución:

Sea AB la cuerda de una circunferencia de 10 cm de radio, con O como centro de la circunferencia

Sabemos,

∠AOB = 90°

Por lo tanto,

Ángulo del sector mayor = 360° – 90° = 270°

Por lo tanto,

Área del sector principal =

$\frac{270}{360} * \pi * (10)^2 cm^2 \\ = \frac{3}{4} * 3.14 * 100 cm^2 \\ = 75 * 3.14 cm^2 \\ = 235.5 cm^2$

Ahora,

Dibujar OM perpendicular a AB

Asi que,

AM = 1/2 AB y ∠AOM = 1/2×90° = 45°

Ahora,

$\frac{AM}{OA} = \sin 45\degree = \frac{1}{\sqrt2}$

Asi que,

AM = 10/√2

Por tanto, AB = 10√2 cm y también, OM=OA

$\cos 45\degree = 10 * 1/\sqrt2 cm = 5\sqrt2cm$

Asi que,

Area del triangulo OAB = 1/2 * base * altura

$\frac{1}{2}10\sqrt2 * 5\sqrt2 cm^2 = 50 cm^2$

Área del segmento principal requerido = 235,5 cm ² + 50 cm ² = 285,5 cm ²

También,

Área del triángulo OAB = 1/2 × OA × OB

= 1/2 × 10 × 10 cm2 ⁼ 50 ^cm2

Pregunta 8. El radio de un círculo con centro O es de 5 cm (ver figura). Se dibujan dos radios OA y OB en ángulo recto entre sí. Encuentre las áreas de los segmentos formados por la cuerda AB (Tome π = 3.14).

Solución:

Radio del círculo ,r = 5 cm

Como OA y OB están en ángulo recto

Por lo tanto, ∠AOB = 90°

∵ Chord AB hace dos segmentos que son segmento menor y segmento mayor respectivamente.

Ahora,

Área del segmento menor

$r^2(\frac{\pi\theta}{360\degree} -sin\frac{\theta}{2}cos\frac{\theta}{2}) \\ = 5^2(\frac{3.14*90\degree}{360\degree}-sin\frac{90\degree}{2}cos\frac{90\degree}{2}) \\ = 25(\frac{3.14*1}{4}-sin45\degree cos45\degree) cm^2 \\ = 25(0.785 - \frac{1}{\sqrt2}*\frac{1}{\sqrt2}) \\ = 25(0.785 - 1/2) cm^2 \\ = 25(0.785-0.5) \\= 7.125 cm^2$

Área del círculo = pi * r ² = 78,50 cm ²

Por lo tanto, área del segmento principal = 71.375 unidades cuadradas.

Pregunta 9. AB es el diámetro de un círculo, centro O. C es un punto de la circunferencia tal que ∠COB = 0. El área del segmento menor cortado por AC es igual al doble del área del sector BOC. Pruebalo.

$sin \frac{\theta}{2} cos \frac{\theta}{2} = \pi (\frac{1}{2} - \frac{\theta}{120})$

Solución:

Dado,

∠AOC = 180° – θ

Supongamos que r es el radio del círculo.

Área del sector BOC = $\pi r^2 * \frac{\theta}{360\degree}$

Ahora,

Área del segmento menor AC = 2 * Área del sector BOC

$\frac{2\pi r^2}{360\degree} = r^2(\frac{\pi(180\degree - \theta}{360\degree}-sin\frac{180\degree-\theta}{2}cos\frac{180\degree-\theta}{2}) \\ \frac{2\pi\theta}{360\degree}$

$2 * \pi r^2 \frac{\theta}{360\degree} = \frac{2\pi r^2 \theta}{360 \degree}$

Pero, Área del segmento = $(\frac{\pi(180\degree - \theta}{360\degree}-sin\frac{180\degree-\theta}{2}cos\frac{180\degree-\theta}{2})r^2$

Ahora, $\frac{2\pi r^2}{360\degree} = r^2(\frac{\pi(180\degree - \theta}{360\degree}-sin\frac{180\degree-\theta}{2}cos\frac{180\degree-\theta}{2}) \\ \frac{2\pi\theta}{360\degree}$

También,

$\\ \frac{2\pi\theta}{360\degree} = \frac{\pi(180\degree-\theta}{360\degree} - cos\frac{\theta}{2}sin\frac{\theta}{2} \\ sin\frac{\theta}{2}cos\frac{\theta}{2}= \pi (\frac{180\degree}{360\degree}-\frac{\theta}{360\degree}-frac{2\theta}{360\degree}) \\ sin\frac{\theta}{2}cos\frac{\theta}{2}= \pi (\frac{1}{2}-\frac{3\theta}{360\degree}) \\ \pi (\frac{1}{2}-\frac{\theta}{120})$

Pregunta 10. Una cuerda de un círculo subtiende un ángulo de 0 en el centro del círculo. El área del segmento menor cortado por la cuerda es un octavo del área del círculo. Pruebalo

$8 sin \frac{\theta}{2} \cos{2}{\theta} + \pi = \frac{\pi\theta}{45}$

Solución:

Sea la cuerda AB que subtiende un ángulo de 0° en el centro de una circunferencia de radio r

Ahora área del círculo = nr ¹ y área del segmento menor ACB.

Pero.

Área del segmento menor ACB = 1/8 = área del círculo

$\pi r^2 = 8 \\ \pi r^2 = 8r^2 (\frac{\pi\theta}{360\degree} - sin\frac{\theta}{2}cos\frac{\theta}{2} \\ \pi = \frac{8\pi\theta}{360} - 8 sin\frac{\theta}{2}cos\frac{\theta}{2} \\ 8 sin \frac{\theta}{2}cos\frac{\theta}{2}+\pi = \frac{8\pi\theta}{360} = \frac{\pi\theta}{45}$

Publicación traducida automáticamente

Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. AB es una cuerda de un círculo con centro O y radio 4 cm. AB tiene una longitud de 4 cm y divide el círculo en dos segmentos. Encuentra el área del segmento menor.

Pregunta 2. Una cuerda PQ de 12 cm de longitud subtiende un ángulo de 120o en el centro de un círculo. Encuentre el área del segmento menor cortado por la cuerda PQ.

Pregunta 3. Una cuerda de un círculo de 14 cm de radio forma un ángulo recto en el centro. Encuentra las áreas de los segmentos mayor y menor del círculo.

Pregunta 4. Se dibuja una cuerda de 10 cm de largo en un círculo cuyo radio es de 5√2 cm. Encuentra el área de ambos segmentos.

Pregunta 5. Una cuerda AB de un círculo de 14 cm de radio forma un ángulo de 60° en el centro de un círculo. Encuentra el área del segmento menor del círculo.

Pregunta 6. Halla el área del segmento menor de un círculo de radio 14 cm, cuando el ángulo del sector correspondiente es de 60°. [Ejemplo Ncert]

Pregunta 7. Una cuerda de un círculo de 20 cm de radio subtiende un ángulo de 90° en el centro. Encuentre el área del segmento mayor correspondiente del círculo. (Use π = 3.14) [Ncert Ejemplar]

Pregunta 8. El radio de un círculo con centro O es de 5 cm (ver figura). Se dibujan dos radios OA y OB en ángulo recto entre sí. Encuentre las áreas de los segmentos formados por la cuerda AB (Tome π = 3.14).

Pregunta 9. AB es el diámetro de un círculo, centro O. C es un punto de la circunferencia tal que ∠COB = 0. El área del segmento menor cortado por AC es igual al doble del área del sector BOC. Pruebalo.

Pregunta 10. Una cuerda de un círculo subtiende un ángulo de 0 en el centro del círculo. El área del segmento menor cortado por la cuerda es un octavo del área del círculo. Pruebalo

Deja una respuesta Cancelar la respuesta