Pregunta 11. Los radios de dos círculos son 19 cm y 9 cm respectivamente. Encuentra el radio y el área del círculo que tiene circunferencias es igual a la suma de la circunferencia de dos círculos.
Solución:
Radio del círculo 1 = r 1 = 19 cm
Radio del círculo 2 = r 2 = 9 cm
Entonces, C 1 = 2πr 1, C 2 = 2πr 2
do = do 1 + do 2
2πr = 2πr 1 + 2πr 2
r = r 1 + r 2
r = 19 + 9
r = 28 cm
Por lo tanto, el radio del círculo = 28 cm
Por lo tanto, área del círculo requerido = πr 2
= (22/7) × 28 × 28
= 2464cm2
Pregunta 12. El área de un patio circular es de 22176 m 2 . Encuentre el costo de cercar este terreno a razón de ₹ 50 por metro.
Solución:
Área del patio circular = 22176 m 2
Área = πr 2
πr2 = 22176
r2 = 22176(7/22)
= 7056
r = 84 metros
Circunferencia del suelo = 2πr
= 2(22/7)84
= 528 metros
Costo de cercado 528 m = ₹ 50 x 528
= ₹ 26400
Por lo tanto, el costo de cercar el suelo = ₹ 26400.
Pregunta 13. El lado de un cuadrado mide 10 cm. Encuentra el área de los círculos inscritos y circunscritos.
Solución:
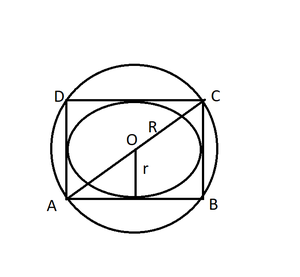
Diagonal del cuadrado = AC = √2 x lado
= 10√2 centímetros
Radio del círculo circunscrito = Diagonal/2
R = 5√2cm
R = 7,07 cm
Área= πR 2
= (22/7) × 7,07 × 7,07
= 157,09 cm2
Por lo tanto, el Área del círculo Circunscrito = 157,09 cm 2
Para círculo inscrito diámetro del círculo = lado del cuadrado = AB
Radio = lado del cuadrado/2
= 10/2
r = 5 metros
Área = πr 2
= (22/7) × 5 × 5
= 78,5 cm2
Por tanto, el área del círculo circunscrito = 157,09 cm 2 y el área del círculo inscrito = 78,5 cm 2 .
Pregunta 14. Si un cuadrado está inscrito en un círculo, encuentra la razón de las áreas del círculo y el cuadrado.
Solución:
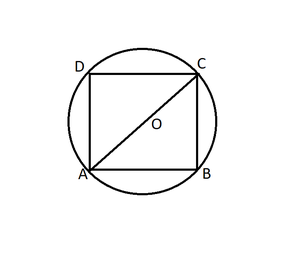
Sea x cm el lado del cuadrado AB que está inscrito en una circunferencia.
Radio del círculo (r) = 1/2 (diagonal del cuadrado)
= 1/2(a√2)
r = a/√2
Área del cuadrado = a 2
Área del círculo = πr 2
= π(a 2 /2)
Razón de áreas = Área del círculo: Área del cuadrado
= π(un 2 /2) : un 2
= π : 2
Por tanto, la razón de las áreas del círculo y del cuadrado = π : 2
Pregunta 15. El área del círculo inscrito en un triángulo equilátero es 154 cm 2 . Encuentra el perímetro del triángulo.
Solución:
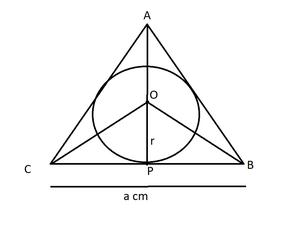
Área de un círculo = πr 2
(22/7) × r2 = 154
r2 = (154 x 7)/22
= 7 × 7
= 49
r = 7 cm
OP es la bisectriz perpendicular de BC (ya que BP es tangente y es un triángulo equilátero)
PA = ½ x BC
Considere que el lado del triángulo equilátero es un cm.
En el triángulo rectángulo OPB
OB 2 = OP 2 + BP 2 (Por el teorema de Pitágoras)
OB 2 = r 2 + (a/2) 2 (BP es la mitad de a)
OB 2 = 49 + un 2 /4
OB = √(49 + a 2 /2) ….. (1)
AP = (√3/2)a (altura de un triángulo equilátero)
OA = (√3/2)a – r
Similarmente
OB = (√3/2)a – r …. (2)
De (1) y (2)
Cuadrando ambos lados
49 + a 2 /4 = (3/4)a 2 + r 2 – √3ar
r = 7
49 + un 2 /4 = (3/4) un 2 + 49 – 7√3a
a 2 /4- (3/4)a 2 = -7√3a
Tomando 4 como MCM
(a 2 – 3a 2 ) / 4 = -7√3a
-2a 2 /4 = -7√3a
a = 14√3cm
Perímetro del triángulo equilátero = 3a
= 42√3
Por tanto, el perímetro del triángulo = 42(1,73)
= 72,7 centímetros
Publicación traducida automáticamente
Artículo escrito por kashika1145 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA