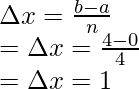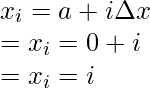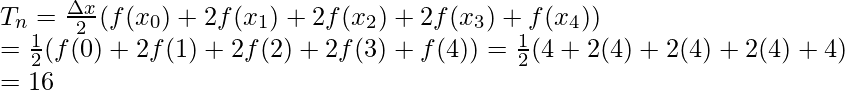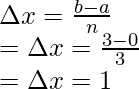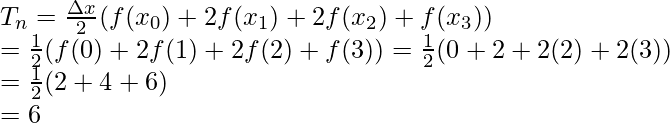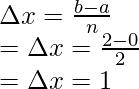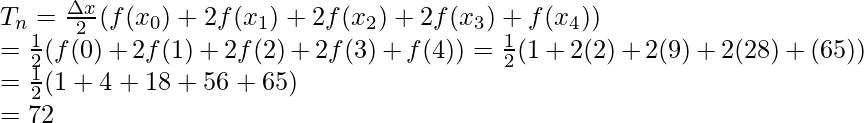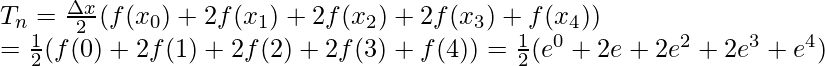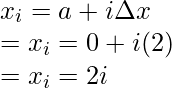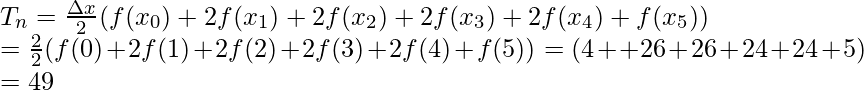Las sumas de Riemann se utilizan para aproximar un área bajo la curva. El área bajo la curva se divide en rectángulos, luego se calcula el área de los rectángulos individuales y su suma da el área total. Este método de aproximación también se puede utilizar para llegar a la definición de las integrales. La regla trapezoidal utiliza un enfoque similar. En esta regla, el área bajo la curva se divide en muchos trapecios cuyo área se calcula y se suma para obtener una aproximación del área total.
Sumas trapezoidales
Esta regla es una de las reglas más importantes en la teoría de la integración. Cualquier área que se va a calcular se divide en muchas partes. Como sugiere el nombre, el área esta vez está dividida en una forma trapezoidal. Para una función f(x), el área encerrada por la función y el eje x se da en la siguiente figura. El objetivo es calcular el área entre x = a y x = b.
Ahora, dividamos el área bajo la curva entre los límites en diferentes trapecios.
Observe que todavía queda algo de área. Esto significa que esta regla es una aproximación, pero la diferencia entre el área real y el área aproximada disminuye a medida que aumenta el número de trapecios. En teoría, cuando el número de trapecios alcanza el infinito, el área aproximada se vuelve igual al área real.
Considere la función f(x) dada en la figura anterior. Sea f(x) continua en el intervalo. Este intervalo se divide en n intervalos iguales, entonces el ancho de cada intervalo se convierte en,
![]()
tal que,
a = x 0 < x 1 < x 2 < …. x norte = segundo
Conocemos el área de un trapezoide = ![]()
Entonces, el área total de la función bajo esta aproximación será,
![]()
Reordenando la ecuación anterior,
![]()
Ahora, a medida que aumenta el número de trapecios, la suma se acerca más al área actual.
![]()
aquí, ![]() y
y ![]()
Notación de suma de la regla trapezoidal
Sabemos que el área de un trapezoide es básicamente el promedio de las longitudes de los lados paralelos multiplicado por la altura. Entonces, en este caso, considere un trapezoide para el i -ésimo intervalo,
![]()
Como el área total es la suma de todas las áreas,
UNA = UNA 1 + UNA 2 + ….+ UNA norte
un = ![]()
⇒A = ![]()
Esto se llama la notación sigma de las sumas trapezoidales.
Sumas de Riemann
Al igual que en el caso anterior, Riemann resume el trabajo sobre la idea de dividir el área bajo la curva en diferentes partes rectangulares. A medida que aumenta el número de rectángulos, el área se acerca cada vez más al área actual. En la figura que se muestra a continuación, hay una función f(x). El área bajo esta función se divide en muchos rectángulos. El área total bajo la curva es la suma de las áreas de todos los rectángulos.

Observe que aquí, el extremo derecho de los rectángulos toca la curva. Esto se llama sumas de Riemann por la derecha. En otro caso, cuando el extremo izquierdo de los rectángulos toca la curva, se les llama sumas de Riemann por la izquierda. La siguiente figura muestra un ejemplo de la suma de Riemann por la izquierda.

Digamos que ![]() es el ancho del intervalo y n es el número de intervalos como se declaró anteriormente. Entonces la suma está dada por,
es el ancho del intervalo y n es el número de intervalos como se declaró anteriormente. Entonces la suma está dada por,
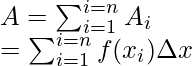
Sumas de punto medio: notación de suma
En las sumas de Riemann, el extremo izquierdo o derecho del rectángulo toca la curva. En este caso, el punto medio del rectángulo toca la curva. Todo lo demás es igual que las sumas de Riemann. La siguiente figura muestra la función f(x) y diferentes rectángulos en las sumas del punto medio.

Digamos que A i denota el área del i -ésimo rectángulo. El área de este rectángulo en este caso será,
![]()
Ahora, el área total en la notación de suma será,

Veamos algunos ejemplos de problemas relacionados con la regla del trapezoide.
Problemas de muestra
Pregunta 1: Encuentra el área encerrada por la función f(x) entre x = 0 a x = 4 con 4 intervalos.
f(x) = 4
Solución:
Aquí a = 0, b = 4 y n = 4.
La regla trapezoidal para n = 4 es,
Sustituyendo los valores en esta ecuación,
Pregunta 2: Encuentra el área encerrada por la función f(x) entre x = 0 a x = 3 con 3 intervalos.
f(x) = x
Solución:
Aquí a = 0, b = 3 y n = 3.
La regla trapezoidal para n = 3 es,
Sustituyendo los valores en esta ecuación,
Pregunta 3: Encuentra el área encerrada por la función f(x) entre x = 0 a x = 2 con 2 intervalos.
f(x) = 2x
Solución:
Aquí a = 0, b = 2 y n = 2.
La regla trapezoidal para n = 2 es,
Sustituyendo los valores en esta ecuación,
Pregunta 4: Encuentra el área encerrada por la función f(x) entre x = 0 a x = 3 con 3 intervalos.
f(x) = x2
Solución:
Aquí a = 0, b = 3 y n = 3.
La regla trapezoidal para n = 3 es,
Sustituyendo los valores en esta ecuación,
Pregunta 5: Encuentra el área encerrada por la función f(x) entre x = 0 a x = 4 con 4 intervalos.
f(x) = x3 + 1
Solución:
Aquí a = 0, b = 4 y n = 4.
La regla trapezoidal para n = 4 es,
Sustituyendo los valores en esta ecuación,
Pregunta 6: Encuentra el área encerrada por la función f(x) entre x = 0 ax = 4 con 4 intervalos.
f(x) = e x
Solución:
Aquí a = 0, b = 4 y n = 4.
La regla trapezoidal para n = 4 es,
Sustituyendo los valores en esta ecuación,
Pregunta 7: Encuentra el área encerrada por la función f(x) dada a continuación entre x = 0 a x = 10 con 5 intervalos.
Solución:
Aquí a = 0, b = 10 y n = 5.
La regla trapezoidal para n = 5 es,
De la gráfica se pueden inferir los valores de la función,
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA