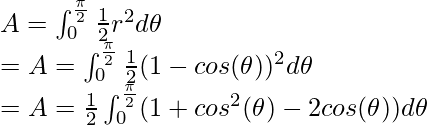Los sistemas de coordenadas permiten la formulación matemática de la posición y comportamiento de un cuerpo en el espacio. Estos sistemas se utilizan en casi todas partes en la vida real. Por lo general, se ve el sistema de coordenadas cartesianas rectangulares, pero hay otro tipo de sistema de coordenadas que es útil para ciertos tipos de curvas. Este sistema de coordenadas es el sistema de coordenadas polares. El sistema de coordenadas polares funciona sobre la base de un ángulo y la distancia desde el origen. Estos sistemas de coordenadas son muy útiles en el caso de formas como espirales, círculos, etc. Se vuelve fundamental estudiar cómo encontrar el área bajo las curvas utilizando este sistema de coordenadas. Veámoslo en detalle.
Sistema de coordenadas polares
Los sistemas de coordenadas no son más que una forma de definir la posición de un punto en el espacio. Un sistema de coordenadas cartesianas o rectangulares utiliza la distancia horizontal (x) y vertical (y) de un punto desde el origen. Hasta ahora, el sistema de coordenadas rectangulares ha sido el centro de todos los conceptos matemáticos. Pero no siempre es fácil manejar coordenadas rectangulares. La posición de un punto también se puede describir usando la distancia (r) de ese punto desde el origen y el ángulo() que forma con el eje x. La siguiente figura muestra la posición de un punto con respecto al origen de ambos sistemas de coordenadas.
Estas coordenadas (r,
Los gráficos polares son las curvas que se definen en los sistemas de coordenadas polares. Las gráficas de las ecuaciones en los sistemas de coordenadas polares se denominan gráficas polares. El concepto del área bajo la curva es el mismo para ambos casos: el sistema de coordenadas rectangulares y el sistema de coordenadas polares. La siguiente figura representa un gráfico polar y la región «A» denota la región entre
Observe que en esta región, el ángulo cambia lentamente. Esta región se puede dividir en sectores muy pequeños como se muestra en la siguiente figura. La suma del área de estos sectores será el área encerrada por la curva.
Para encontrar el área total, considera un sector. El área de un sector en un círculo está dada por,
![]()
Ahora, como el ángulo es muy pequeño, se puede escribir como d
![]()
El área total de la región está dada por la suma de todos esos rectángulos,
![]()
Esto se puede reescribir como,
![]()
Área encerrada por un cardioide
Una cardioide es una curva polar que se asemeja a la forma de un corazón. La forma del cardioide también se puede comparar con la forma de una manzana. Es una curva que se define como el lugar geométrico de un punto que se encuentra sobre la circunferencia de una circunferencia que rueda sin deslizamiento alguno. El gráfico y la ecuación de la curva se dan a continuación,
r = 1 + cos(
o
r= 1 – cos(
En este caso, a = 0 y b = 90° y r = 1 – cos(
Introduciendo estos valores en la fórmula,
Reordenando la ecuación con la identidad cos(2θ) = 1 – 2cos 2 (θ)
un =
un =
un =
Todos los conceptos y métodos que se aplican para calcular diferentes áreas en los sistemas cartesianos se pueden extender fácilmente a los gráficos polares. Considere dos gráficos polares que están dados por, r = 3sin(
La región común se puede dividir en dos partes iguales por la línea que pasa como se muestra en la siguiente figura. El área de la intersección será,
un = ![Rendered by QuickLaTeX.com \frac{1}{2}\int^{\frac{\pi}{4}}_{0}(r^2d\theta) \\ = \frac{1}{2}\int^{\frac{\pi}{4}}_{0}(3^2sin^2(\theta))d\theta \\ = \frac{9}{2}\int^{\frac{\pi}{4}}_{0}sin^2(\theta)d\theta \\ = \frac{9}{4}\int^{\frac{\pi}{4}}_{0}(1 - cos(2\theta))d\theta \\ = \frac{9}{4}[ \theta - \frac{sin(2\theta)}{2}]^{\frac{\pi}{4}}_{0} \\ = \frac{9}{4}[\frac{\pi}{4} - \frac{1}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1c055341c7c7d2558008292a41042d97_l3.png)
El área total será el doble del área calculada.
Problemas de muestra
Pregunta 1: Encuentra el área encerrada por la curva r = 3 en el primer cuadrante.
Responder:
La ecuación dada es la ecuación de un círculo. El área se puede calcular usando la fórmula estudiada anteriormente,
un =
un =
un =
un =
Pregunta 2: Encuentra el área encerrada por la curva r = 5 + en los dos primeros cuadrantes.
Responder:
La ecuación dada es la ecuación de un círculo. El área se puede calcular usando la fórmula estudiada anteriormente,
un =
un =
un =
un =
un =
Pregunta 3: Encuentra el área encerrada por la curva r = 5 + e en los dos primeros cuadrantes.
Responder:
La ecuación dada es la ecuación de un círculo. El área se puede calcular usando la fórmula estudiada anteriormente,
un =
un =
un =
un =
un =
En este caso, a = 0 y b = 180° y r = 1 + cos(θ)
Introduciendo estos valores en la fórmula,
Reordenando la ecuación con la identidad cos(2θ) = 1 – 2cos 2 (θ)
un =
un =
un =
un =
Pregunta 5: Encuentra el área fuera del círculo r = 3 y dentro del círculo r = 5.
Responder:
La ecuación dada es la ecuación de un círculo. El área se puede calcular usando la fórmula estudiada anteriormente,
Área del círculo mayor,
un 5 =
un 5 =
un 5 =
un 5 =
El área del círculo más pequeño será,
un 3 =
un 3 =
un 3 =
un 3 =
El área de la región común será,
UN = UN 5 – UN 3
A = 50π – 9π
A = 41π
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA