Regresión lineal (Implementación de Python)

Este artículo analiza los conceptos básicos de la regresión lineal y su implementación en el lenguaje de programación Python.
La regresión lineal es un método estadístico para modelar relaciones entre una variable dependiente con un conjunto dado de variables independientes.

Nota: En este artículo, nos referimos a las variables dependientes como respuestas y a las variables independientes como características para simplificar.
Para proporcionar una comprensión básica de la regresión lineal, comenzamos con la versión más básica de la regresión lineal, es decir, la regresión lineal simple .

Regresión lineal simple

La regresión lineal simple es un enfoque para predecir una respuesta usando una característica única .
Se supone que las dos variables están linealmente relacionadas. Por lo tanto, tratamos de encontrar una función lineal que prediga el valor de respuesta (y) con la mayor precisión posible como función de la característica o variable independiente (x).
Consideremos un conjunto de datos donde tenemos un valor de respuesta y para cada característica x:

Para generalizar, definimos:
x como vector de características , es decir, x = [x_1, x_2, …., x_n],
y como vector de respuesta , es decir, y = [y_1, y_2, …., y_n]
para n observaciones (en el ejemplo anterior , n=10).
Un diagrama de dispersión del conjunto de datos anterior se parece a: –

Ahora, la tarea es encontrar una línea que encaje mejor en el diagrama de dispersión anterior para que podamos predecir la respuesta para cualquier valor de característica nueva. (es decir, un valor de x no presente en un conjunto de datos)
Esta línea se llama línea de regresión .
La ecuación de la línea de regresión se representa como:
$h(x_i) = \beta _0 + \beta_1x_i$

Aquí,

h(x_i) representa el valor de respuesta pronosticado para la i- ^ésima observación.
b_0 y b_1 son coeficientes de regresión y representan la intersección y y la pendiente de la línea de regresión, respectivamente.

Para crear nuestro modelo, debemos “aprender” o estimar los valores de los coeficientes de regresión b_0 y b_1. Y una vez que hayamos estimado estos coeficientes, ¡podemos usar el modelo para predecir las respuestas!
En este artículo, vamos a utilizar el principio de los mínimos cuadrados .
Ahora considere:
$y_i = \beta_0 + \beta_1x_i + \varepsilon_i = h(x_i) + \varepsilon_i \Rightarrow \varepsilon_i = y_i -h(x_i)$
Aquí, e_i es un error residual en i-ésima observación.
Por lo tanto, nuestro objetivo es minimizar el error residual total.
Definimos el error al cuadrado o función de costo, J como: ¡
$J(\beta_0,\beta_1)= \frac{1}{2n} \sum_{i=1}^{n} \varepsilon_i^{2}$
y nuestra tarea es encontrar el valor de b_0 y b_1 para el cual J(b_0,b_1) es mínimo!
Sin entrar en detalles matemáticos, presentamos el resultado aquí:
$\beta_1 = \frac{SS_{xy}}{SS_{xx}}$
$\beta_0 = \bar{y} - \beta_1\bar{x}$
donde SS_xy es la suma de las desviaciones cruzadas de y y x:
$SS_{xy} = \sum_{i=1}^{n} (x_i-\bar{x})(y_i-\bar{y}) = \sum_{i=1}^{n} y_ix_i - n\bar{x}\bar{y}$
y SS_xx es la suma de las desviaciones al cuadrado de x:
$SS_{xx} = \sum_{i=1}^{n} (x_i-\bar{x})^2 = \sum_{i=1}^{n}x_i^2 - n(\bar{x})^2$
Nota: La derivación completa para encontrar estimaciones de mínimos cuadrados en regresión lineal simple se puede encontrar aquí .

Código: implementación de Python de la técnica anterior en nuestro pequeño conjunto de datos

Python

import numpy as np
import matplotlib.pyplot as plt
  
def estimate_coef(x, y):
    # number of observations/points
    n = np.size(x)
  
    # mean of x and y vector
    m_x = np.mean(x)
    m_y = np.mean(y)
  
    # calculating cross-deviation and deviation about x
    SS_xy = np.sum(y*x) - n*m_y*m_x
    SS_xx = np.sum(x*x) - n*m_x*m_x
  
    # calculating regression coefficients
    b_1 = SS_xy / SS_xx
    b_0 = m_y - b_1*m_x
  
    return (b_0, b_1)
  
def plot_regression_line(x, y, b):
    # plotting the actual points as scatter plot
    plt.scatter(x, y, color = "m",
               marker = "o", s = 30)
  
    # predicted response vector
    y_pred = b[0] + b[1]*x
  
    # plotting the regression line
    plt.plot(x, y_pred, color = "g")
  
    # putting labels
    plt.xlabel('x')
    plt.ylabel('y')
  
    # function to show plot
    plt.show()
  
def main():
    # observations / data
    x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
    y = np.array([1, 3, 2, 5, 7, 8, 8, 9, 10, 12])
  
    # estimating coefficients
    b = estimate_coef(x, y)
    print("Estimated coefficients:\nb_0 = {}  \
          \nb_1 = {}".format(b[0], b[1]))
  
    # plotting regression line
    plot_regression_line(x, y, b)
  
if __name__ == "__main__":
    main()

Producción:

Estimated coefficients:
b_0 = -0.0586206896552
b_1 = 1.45747126437

Y el gráfico obtenido se ve así:

Regresión lineal múltiple

La regresión lineal múltiple intenta modelar la relación entre dos o más características y una respuesta ajustando una ecuación lineal a los datos observados.
Claramente, no es más que una extensión de la regresión lineal simple.
Considere un conjunto de datos con características p (o variables independientes) y una respuesta (o variable dependiente).
Además, el conjunto de datos contiene n filas/observaciones.
Definimos:
X ( array de características ) = una array de tamaño n X p donde x_{ij} denota los valores de j-ésima característica para la i-ésima observación.
Entonces,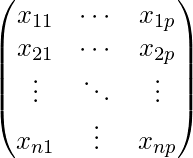
$\begin{pmatrix} x_{11} & \cdots & x_{1p} \\ x_{21} & \cdots & x_{2p} \\ \vdots & \ddots & \vdots \\ x_{n1} & \vdots & x_{np} \end{pmatrix}$
y
( vector de respuesta ) = un vector de tamaño ndonde y_{i} denota el valor de la respuesta para la i-ésima observación.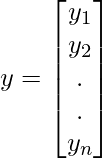
$y = \begin{bmatrix} y_1\\ y_2\\ .\\ .\\ y_n \end{bmatrix}$
La línea de regresión para características p se representa como:
$h(x_i) = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + .... + \beta_px_{ip}$
donde h(x_i) es el valor de respuesta pronosticado para i-ésima observación y b_0, b_1, …, b_p son los coeficientes de regresión .
Además, podemos escribir: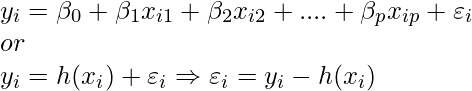
$\newline y_i = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + .... + \beta_px_{ip} + \varepsilon_i \newline or \newline y_i = h(x_i) + \varepsilon_i \Rightarrow \varepsilon_i = y_i - h(x_i)$
donde e_i representa el error residual en la i-ésima observación.
Podemos generalizar nuestro modelo lineal un poco más representando la array de características X como:
$X = \begin{pmatrix} 1 & x_{11} & \cdots & x_{1p} \\ 1 & x_{21} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & \cdots & x_{np} \end{pmatrix}$
Así que ahora, el modelo lineal se puede expresar en términos de arrays como:
$y = X\beta + \varepsilon$
donde,
$\beta = \begin{bmatrix} \beta_0\\ \beta_1\\ .\\ .\\ \beta_p \end{bmatrix}$
y
$\varepsilon = \begin{bmatrix} \varepsilon_1\\ \varepsilon_2\\ .\\ .\\ \varepsilon_n \end{bmatrix}$
Ahora, determinamos una estimación de b , es decir, b’ usando elLeast Squares method.
As already explained, the Least Squares method tends to determine b’ for which total residual error is minimized.
We present the result directly here:
$\hat{\beta} = ({X}'X)^{-1} {X}'y$
where ‘ represents the transpose of the matrix while -1 represents the matrix inverse.
Knowing the least square estimates, b’, the multiple linear regression model can now be estimated as:
$\hat{y} = X\hat{\beta}$
where y’ is the estimated response vector.
Note: The complete derivation for obtaining least square estimates in multiple linear regression can be found here.

Código: implementación de Python de múltiples técnicas de regresión lineal en el conjunto de datos de precios de viviendas de Boston utilizando Scikit-learn.

Python

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metrics
  
# load the boston dataset
boston = datasets.load_boston(return_X_y=False)
  
# defining feature matrix(X) and response vector(y)
X = boston.data
y = boston.target
  
# splitting X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4,
                                                    random_state=1)
  
# create linear regression object
reg = linear_model.LinearRegression()
  
# train the model using the training sets
reg.fit(X_train, y_train)
  
# regression coefficients
print('Coefficients: ', reg.coef_)
  
# variance score: 1 means perfect prediction
print('Variance score: {}'.format(reg.score(X_test, y_test)))
  
# plot for residual error
  
## setting plot style
plt.style.use('fivethirtyeight')
  
## plotting residual errors in training data
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
            color = "green", s = 10, label = 'Train data')
  
## plotting residual errors in test data
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
            color = "blue", s = 10, label = 'Test data')
  
## plotting line for zero residual error
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
  
## plotting legend
plt.legend(loc = 'upper right')
  
## plot title
plt.title("Residual errors")
  
## method call for showing the plot
plt.show()

Producción:

Coefficients:
[ -8.80740828e-02   6.72507352e-02   5.10280463e-02   2.18879172e+00
-1.72283734e+01   3.62985243e+00   2.13933641e-03  -1.36531300e+00
2.88788067e-01  -1.22618657e-02  -8.36014969e-01   9.53058061e-03
-5.05036163e-01]
Variance score: 0.720898784611

y el diagrama de error residual se ve así:

En el ejemplo anterior, determinamos la puntuación de precisión utilizando la puntuación de varianza explicada .
Definimos:
puntuación_de_varianza_explicada = 1 – Var{y – y’}/Var{y}
donde y’ es el resultado objetivo estimado, y el resultado objetivo correspondiente (correcto) y Var es la varianza, el cuadrado de la desviación estándar.
La mejor puntuación posible es 1,0, los valores más bajos son peores.

Suposiciones:

A continuación se presentan las suposiciones básicas que hace un modelo de regresión lineal con respecto a un conjunto de datos en el que se aplica:

Relación lineal : la relación entre la respuesta y las variables de característica debe ser lineal. La suposición de linealidad se puede probar usando diagramas de dispersión. Como se muestra a continuación, la primera figura representa variables linealmente relacionadas, mientras que las variables en la segunda y tercera figura probablemente no sean lineales. Entonces, la primera figura dará mejores predicciones usando regresión lineal.

Poca o ninguna multicolinealidad : se supone que hay poca o ninguna multicolinealidad en los datos. La multicolinealidad ocurre cuando las características (o variables independientes) no son independientes entre sí.
Poca o ninguna autocorrelación : otra suposición es que hay poca o ninguna autocorrelación en los datos. La autocorrelación ocurre cuando los errores residuales no son independientes entre sí. Puede consultar aquí para obtener más información sobre este tema.
Homocedasticidad : la homocedasticidad describe una situación en la que el término de error (es decir, el «ruido» o perturbación aleatoria en la relación entre las variables independientes y la variable dependiente) es el mismo en todos los valores de las variables independientes. Como se muestra a continuación, la figura 1 tiene homocedasticidad mientras que la figura 2 tiene heterocedasticidad.

Al llegar al final de este artículo, analizamos algunas aplicaciones de la regresión lineal a continuación.

Aplicaciones:

Líneas de tendencia: una línea de tendencia representa la variación de los datos cuantitativos con el paso del tiempo (como el PIB, los precios del petróleo, etc.). Estas tendencias suelen seguir una relación lineal. Por lo tanto, la regresión lineal se puede aplicar para predecir valores futuros. Sin embargo, este método adolece de una falta de validez científica en los casos en que otros cambios potenciales pueden afectar los datos.
Economía: La regresión lineal es la herramienta empírica predominante en economía. Por ejemplo, se utiliza para predecir el gasto del consumidor, el gasto de inversión fija, la inversión en inventarios, las compras de exportaciones de un país, el gasto en importaciones, la demanda para mantener activos líquidos, la demanda laboral y la oferta laboral.
Finanzas: el modelo de activos de precio de capital utiliza la regresión lineal para analizar y cuantificar los riesgos sistemáticos de una inversión.
4. Biología: la regresión lineal se usa para modelar relaciones causales entre parámetros en sistemas biológicos.

Referencias:

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Regresión lineal simple

Python

Regresión lineal múltiple

Python

Suposiciones:

Aplicaciones:

Referencias:

Deja una respuesta Cancelar la respuesta