Pregunta 1. En un triángulo OAB, si P, Q son puntos de trisección de AB, Demostrar que OP 2 + OQ 2 = 5/9 AB 2 .
Solución:
Dado que en el triángulo OAB,
∠AOB = 90°, y P, Q son puntos de trisección de AB.
Considere ‘O’ como origen, los vectores de posición de A y B son
y
respectivamente.
Como P y Q son puntos de trisección de AB, AP:PB = 1:2 y AQ:QB = 2:1.
De la fórmula de la sección, el vector de posición de P es
El vector de posición de Q es
Ahora, OP 2 + OQ 2 =
⇒
⇒
Sabemos que
, ya que
y
son perpendiculares.
⇒
Usando el teorema de Pitágoras, obtenemos
Por lo tanto probado.
Pregunta 2. Demuestra que si las diagonales de un cuadrilátero se bisecan en ángulo recto, entonces es un rombo.
Solución:
Consideremos que OABC es un cuadrilátero y las diagonales AB y OC se bisecan a 90°.
Considere ‘0’ como origen y los vectores de posición de A y B están dados por
y
respectivamente.
Ahora, el vector de posición de E es
Usando la ley del triángulo de la suma de vectores,
⇒
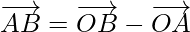
⇒
Como las diagonales se bisecan a 90°,
⇒
⇒
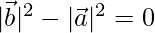
⇒ |
⇒OA = OB
Por lo tanto, probamos que los lados adyacentes del cuadrilátero son iguales si sus diagonales se bisecan a 90°.
Pregunta 3. Demostrar por el método vectorial que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (Teorema de Pitágoras).
Solución:
Consideremos que ABC es el triángulo rectángulo con ∠BAC = 90°.
Considere ‘A’ como origen y los vectores de posición
Como AB y AC son perpendiculares entre sí,
Ahora, AB 2 + AC 2 =
…(1)
De la ley del triángulo de la suma de vectores,
⇒
⇒
Ahora, BC 2 =
⇒
⇒
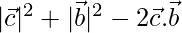
⇒
…(2)
Por lo tanto, de eq(1) y eq(2) obtenemos,
⇒
Por lo tanto probado.
Pregunta 4. Demostrar por el método vectorial que la suma de los cuadrados de las diagonales del paralelogramo es igual a la suma de los cuadrados de sus lados.
Solución:
Consideremos ABCD como un paralelogramo y AC, BD como sus diagonales.
Considere A como origen, Deje que los vectores de posición de AB, AD sean
respectivamente.
Usando la ley del triángulo de la suma de vectores, tenemos
⇒
⇒
En el triángulo ABC,
Ahora, cuadrados de lados del paralelogramo =
⇒
⇒
⇒
…(1)
Además, cuadrados de diagonales =
⇒
⇒
⇒
…(2)
Por, observando eq(1) y eq(2),
Probamos que la suma de los cuadrados de los lados de un paralelogramo es igual a la suma de los cuadrados de sus diagonales.
Pregunta 5. Demostrar mediante el método vectorial que el cuadrilátero obtenido al unir los puntos medios de los lados adyacentes del rectángulo es un rombo.
Solución:
Consideremos que ABCD es un rectángulo y P, Q, R, S son puntos medios de AB, BC, CD, DA respectivamente.
Considere A como origen, los vectores de posición de AB, AD son
respectivamente.
Ahora, usando la ley del triángulo de la suma de vectores,
⇒
⇒
Similarmente,
⇒
⇒
Al observar, encontramos que PQ || SR, entonces podemos decir que es un paralelogramo
Hallemos si forma un rombo calculando la longitud de los lados adyacentes,
⇒
…(1)
También, de la figura,
⇒
⇒
⇒
…(2)
De eq(1) y eq(2) PQ y PS son lados adyacentes y |PQ|=|PS|,
entonces PQRS es un rombo.
Por lo tanto, Por lo tanto demostrado
Pregunta 6. Demuestra que las diagonales de un rombo son bisectrices perpendiculares entre sí.
Solución:
Consideremos que OABC es un rombo, OB y AC son diagonales de rombo.
Considere O como origen, los vectores de posición de OA y OC son
respectivamente.
De figura,
⇒
De figura,
⇒
Ahora,
⇒
Sabemos que los lados adyacentes son iguales en un rombo,
⇒
Por lo tanto, las diagonales de un rombo son bisectrices perpendiculares entre sí.
Pregunta 7. Demuestra que las diagonales del rectángulo son perpendiculares si y solo si el rectángulo es un cuadrado.
Solución:
Consideremos que ABCD es un rectángulo, AC, BD son diagonales del rectángulo.
Considere A como origen, los vectores de posición de AB, AD son
respectivamente.
De figura,
⇒
Similarmente,
⇒
Si las diagonales son perpendiculares, entonces
⇒
⇒
⇒
Por lo tanto, si las diagonales de un rectángulo son perpendiculares, entonces es un cuadrado.
Pregunta 8. Si AD es la mediana del triángulo ABC, prueba con vectores que
Solución:
Consideremos que ABC es un triángulo y AD es una mediana.
Considere que A es un origen, los vectores de posición de AB y AC lo son
respectivamente.
El vector de posición de AD es
El vector de posición de CD es
⇒
Ahora, AB 2 + AC 2 =
…(1)
Además, 2(AD 2 + CD 2 ) =
⇒
⇒
…(2)
De eq(1) y eq(2), obtenemos
Por lo tanto, Por lo tanto probado.
Pregunta 9. Si la mediana a la base del triángulo es perpendicular a la base, entonces el triángulo es isósceles.
Solución:
Consideremos que ABC es un triángulo y AD es una mediana.
Considere A como origen, el vector de posición de AB, AC son
respectivamente.
Ahora, el vector de posición de AD es
Usando la ley del triángulo de la suma de vectores,
⇒
Como AD y BC son perpendiculares,
⇒
⇒
⇒
⇒
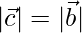
⇒ CA = AB
Por lo tanto, el Triángulo ABC es un triángulo Isósceles.
Pregunta 10. En un cuadrilátero ABCD, demostrar que , donde P, Q son puntos medios de las diagonales AC y BD.
Solución:
Consideremos que ABCD es un cuadrilátero, AC, BD son diagonales.
Considere A como origen, los vectores de posición de AB, AC, AD son
respectivamente.
Sean P y Q los puntos medios de AC, BD.
El vector de posición de P es
El vector de posición de Q es
Ahora, AB 2 + BC 2 + CD 2 + DA 2 =
⇒
⇒
…(1)
Además, AC 2 + BD 2 + 4PQ 2 =
⇒
⇒
⇒
…(2)
De eq(1) y eq(2), obtenemos,
Por lo tanto, Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por srinivasteja18 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA









