Dado un árbol binario (no un árbol de búsqueda binario) y cualquier número de Nodes clave, la tarea es encontrar el ancestro menos común de todos los Nodes clave.
La siguiente es la definición de LCA de Wikipedia :
Sea T un árbol enraizado. El ancestro común más bajo entre dos Nodes n1 y n2 se define como el Node más bajo en T que tiene tanto n1 como n2 como descendientes (donde permitimos que un Node sea descendiente de sí mismo).
El LCA de cualquier número de Nodes en T es el ancestro común compartido de los Nodes que se encuentra más alejado de la raíz.
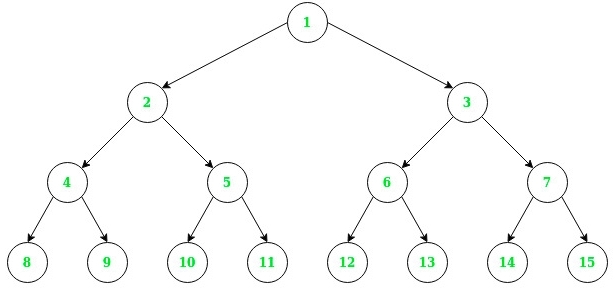
Ejemplo: En la figura anterior:
LCA of nodes 12, 14, 15 is node 3 LCA of nodes 3, 14, 15 is node 3 LCA of nodes 6, 7, 15 is node 3 LCA of nodes 5, 13, 14, 15 is node 1 LCA of nodes 6, 12 is node 6
Enfoque:
El siguiente es el enfoque simple para el ancestro mínimo común para cualquier número de Nodes.
- Para cada Node, calcule el número coincidente de Nodes en ese Node y su subárbol.
- Si root también es un Node coincidente.
MatchingNodes = MatchingNodes en el subárbol izquierdo + MatchingNodes en el subárbol derecho + 1
- Si la raíz no es un Node coincidente.
MatchingNodes = MatchingNodes en el subárbol izquierdo + MatchingNodes en el subárbol derecho
- Si el recuento de Nodes coincidentes en cualquier Node es igual al número de claves, agregue ese Node a la lista de antepasados.
- El primer Node en la lista de antepasados es el antepasado menos común de todas las claves dadas.
A continuación se muestra la implementación del enfoque anterior.
C++
// C++ implementation to find
// Ancestors of any number of nodes
#include <bits/stdc++.h>
using namespace std;
// Tree Class
class TreeNode
{
public:
int data;
TreeNode *left, *right;
TreeNode(int value)
{
this->data = value;
this->left = NULL;
this->right = NULL;
}
};
int getKeysCount(TreeNode *root, vector<int> &keyNodes,
int matchingNodes,
vector<TreeNode *> &ancestors)
{
// Base Case. When root is Null
if (root == NULL)
{
return 0;
}
// Search for left and right subtree
// for matching child Key Node.
matchingNodes += getKeysCount(root->left, keyNodes,
matchingNodes, ancestors) +
getKeysCount(root->right, keyNodes,
matchingNodes, ancestors);
// Condition to check if Root Node
// is also in Key Node
if (find(keyNodes.begin(),
keyNodes.end(), root->data) != keyNodes.end())
{
matchingNodes++;
}
// Condition when matching Nodes is
// equal to the Key Nodes found
if (matchingNodes == keyNodes.size())
{
ancestors.push_back(root);
}
return matchingNodes;
}
// Function to find Least Common
// Ancestors of N number of nodes
TreeNode *lcaOfNodes(TreeNode *root,
vector<int> &keyNodes)
{
// Create a new list for
// capturing all the ancestors
// of the given nodes
vector<TreeNode *> ancestors;
// Initially there is No Matching Nodes
int matchingNodes = 0;
getKeysCount(root, keyNodes,
matchingNodes, ancestors);
// First Node in the Ancestors list
// is the Least Common Ancestor of
// Given keyNodes
return ancestors[0];
}
// Driver Code
int main()
{
// Creation of Tree
TreeNode *root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
root->right->left = new TreeNode(6);
root->right->right = new TreeNode(7);
root->left->left->left = new TreeNode(8);
root->left->left->right = new TreeNode(9);
root->left->right->left = new TreeNode(10);
root->left->right->right = new TreeNode(11);
root->right->left->left = new TreeNode(12);
root->right->left->right = new TreeNode(13);
root->right->right->left = new TreeNode(14);
root->right->right->right = new TreeNode(15);
// Key Nodes for LCA
vector<int> keyNodes;
keyNodes.push_back(12);
keyNodes.push_back(14);
keyNodes.push_back(15);
cout << lcaOfNodes(root, keyNodes)->data
<< endl;
return 0;
}
// This code is contributed by sanjeev2552
Java
// Java implementation to find
// Ancestors of any number of nodes
import java.util.ArrayList;
// Tree Class
class TreeNode {
int data;
TreeNode left;
TreeNode right;
public TreeNode(int value)
{
this.data = value;
left = right = null;
}
}
public class LCAofAnyNumberOfNodes {
// Function to find Least Common
// Ancestors of N number of nodes
public static TreeNode lcaOfNodes(
TreeNode root,
ArrayList<Integer> keyNodes)
{
// Create a new list for
// capturing all the ancestors
// of the given nodes
ArrayList<TreeNode> ancestors =
new ArrayList<TreeNode>();
// Initially there is No Matching Nodes
int matchingNodes = 0;
getKeysCount(root, keyNodes,
matchingNodes, ancestors);
// First Node in the Ancestors list
// is the Least Common Ancestor of
// Given keyNodes
return ancestors.get(0);
}
private static int getKeysCount(
TreeNode root, ArrayList<Integer> keyNodes,
int matchingNodes,
ArrayList<TreeNode> ancestors)
{
// Base Case. When root is Null
if (root == null)
return 0;
// Search for left and right subtree
// for matching child Key Node.
matchingNodes += getKeysCount(root.left,
keyNodes, matchingNodes, ancestors)
+ getKeysCount(root.right,
keyNodes, matchingNodes, ancestors);
// Condition to check if Root Node
// is also in Key Node
if (keyNodes.contains(root.data)){
matchingNodes++;
}
// Condition when matching Nodes is
// equal to the Key Nodes found
if (matchingNodes == keyNodes.size())
ancestors.add(root);
return matchingNodes;
}
// Driver Code
public static void main(String[] args)
{
// Creation of Tree
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right =
new TreeNode(5);
root.right.left =
new TreeNode(6);
root.right.right =
new TreeNode(7);
root.left.left.left =
new TreeNode(8);
root.left.left.right =
new TreeNode(9);
root.left.right.left =
new TreeNode(10);
root.left.right.right =
new TreeNode(11);
root.right.left.left =
new TreeNode(12);
root.right.left.right =
new TreeNode(13);
root.right.right.left =
new TreeNode(14);
root.right.right.right =
new TreeNode(15);
// Key Nodes for LCA
ArrayList<Integer> keyNodes =
new ArrayList<Integer>();
keyNodes.add(12);
keyNodes.add(14);
keyNodes.add(15);
System.out.println(
lcaOfNodes(root, keyNodes).data
);
}
}
Python3
# Python3 implementation to find # Ancestors of any number of nodes # Tree Class class TreeNode: def __init__(self, value): self.data = value self.left = None self.right = None # Create a new list for # capturing all the ancestors # of the given nodes ancestors = [] # Function to find Least Common # Ancestors of N number of nodes def lcaOfNodes(root, keyNodes): # Initially there is No Matching Nodes matchingNodes = 0 getKeysCount(root, keyNodes, matchingNodes) # First Node in the Ancestors list # is the Least Common Ancestor of # Given keyNodes ancestors[0].data-=1 return ancestors[0] def getKeysCount(root, keyNodes, matchingNodes): # Base Case. When root is Null if root == None: return 0 # Search for left and right subtree # for matching child Key Node. matchingNodes += getKeysCount(root.left, keyNodes, matchingNodes) + getKeysCount(root.right, keyNodes, matchingNodes) # Condition to check if Root Node # is also in Key Node if keyNodes: matchingNodes+=1 # Condition when matching Nodes is # equal to the Key Nodes found if matchingNodes == len(keyNodes): ancestors.append(root) return matchingNodes # Creation of Tree root = TreeNode(1) root.left = TreeNode(2) root.right = TreeNode(3) root.left.left = TreeNode(4) root.left.right = TreeNode(5) root.right.left = TreeNode(6) root.right.right = TreeNode(7) root.left.left.left = TreeNode(8) root.left.left.right = TreeNode(9) root.left.right.left = TreeNode(10) root.left.right.right = TreeNode(11) root.right.left.left = TreeNode(12) root.right.left.right = TreeNode(13) root.right.right.left = TreeNode(14) root.right.right.right = TreeNode(15) # Key Nodes for LCA keyNodes = [] keyNodes.append(12) keyNodes.append(14) keyNodes.append(15) tmp = lcaOfNodes(root, keyNodes) print(tmp.data) # This code is contributed by suresh07.
C#
// C# implementation to find
// Ancestors of any number of nodes
using System;
using System.Collections.Generic;
// Tree Class
class TreeNode {
public int data;
public TreeNode left;
public TreeNode right;
public TreeNode(int value)
{
this.data = value;
left = right = null;
}
}
public class LCAofAnyNumberOfNodes {
// Function to find Least Common
// Ancestors of N number of nodes
static TreeNode lcaOfNodes(
TreeNode root,
List<int> keyNodes)
{
// Create a new list for
// capturing all the ancestors
// of the given nodes
List<TreeNode> ancestors =
new List<TreeNode>();
// Initially there is No Matching Nodes
int matchingNodes = 0;
getKeysCount(root, keyNodes,
matchingNodes, ancestors);
// First Node in the Ancestors list
// is the Least Common Ancestor of
// Given keyNodes
return ancestors[0];
}
private static int getKeysCount(
TreeNode root, List<int> keyNodes,
int matchingNodes,
List<TreeNode> ancestors)
{
// Base Case. When root is Null
if (root == null)
return 0;
// Search for left and right subtree
// for matching child Key Node.
matchingNodes += getKeysCount(root.left,
keyNodes, matchingNodes, ancestors)
+ getKeysCount(root.right,
keyNodes, matchingNodes, ancestors);
// Condition to check if Root Node
// is also in Key Node
if (keyNodes.Contains(root.data)){
matchingNodes++;
}
// Condition when matching Nodes is
// equal to the Key Nodes found
if (matchingNodes == keyNodes.Count)
ancestors.Add(root);
return matchingNodes;
}
// Driver Code
public static void Main(String[] args)
{
// Creation of Tree
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right =
new TreeNode(5);
root.right.left =
new TreeNode(6);
root.right.right =
new TreeNode(7);
root.left.left.left =
new TreeNode(8);
root.left.left.right =
new TreeNode(9);
root.left.right.left =
new TreeNode(10);
root.left.right.right =
new TreeNode(11);
root.right.left.left =
new TreeNode(12);
root.right.left.right =
new TreeNode(13);
root.right.right.left =
new TreeNode(14);
root.right.right.right =
new TreeNode(15);
// Key Nodes for LCA
List<int> keyNodes = new List<int>();
keyNodes.Add(12);
keyNodes.Add(14);
keyNodes.Add(15);
Console.WriteLine(
lcaOfNodes(root, keyNodes).data
);
}
}
// This code is contributed by PrinciRaj1992
Javascript
<script>
// JavaScript implementation to find
// Ancestors of any number of nodes
// Tree Class
class TreeNode {
constructor(value)
{
this.data = value;
this.left = null;
this.right = null;
}
}
// Create a new list for
// capturing all the ancestors
// of the given nodes
var ancestors = [];
// Function to find Least Common
// Ancestors of N number of nodes
function lcaOfNodes( root, keyNodes)
{
// Initially there is No Matching Nodes
var matchingNodes = 0;
getKeysCount(root, keyNodes,
matchingNodes);
// First Node in the Ancestors list
// is the Least Common Ancestor of
// Given keyNodes
return ancestors[0];
}
function getKeysCount( root, keyNodes, matchingNodes)
{
// Base Case. When root is Null
if (root == null)
return 0;
// Search for left and right subtree
// for matching child Key Node.
matchingNodes += getKeysCount(root.left,
keyNodes, matchingNodes)
+ getKeysCount(root.right,
keyNodes, matchingNodes);
// Condition to check if Root Node
// is also in Key Node
if (keyNodes.includes(root.data)){
matchingNodes++;
}
// Condition when matching Nodes is
// equal to the Key Nodes found
if (matchingNodes == keyNodes.length)
ancestors.push(root);
return matchingNodes;
}
// Driver Code
// Creation of Tree
var root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right =
new TreeNode(5);
root.right.left =
new TreeNode(6);
root.right.right =
new TreeNode(7);
root.left.left.left =
new TreeNode(8);
root.left.left.right =
new TreeNode(9);
root.left.right.left =
new TreeNode(10);
root.left.right.right =
new TreeNode(11);
root.right.left.left =
new TreeNode(12);
root.right.left.right =
new TreeNode(13);
root.right.right.left =
new TreeNode(14);
root.right.right.right =
new TreeNode(15);
// Key Nodes for LCA
var keyNodes = [];
keyNodes.push(12);
keyNodes.push(14);
keyNodes.push(15);
var tmp = lcaOfNodes(root, keyNodes);
document.write(tmp.data);
</script>
3
Publicación traducida automáticamente
Artículo escrito por Prasun Mondal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA