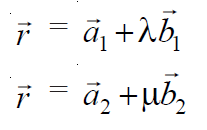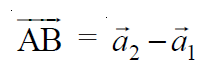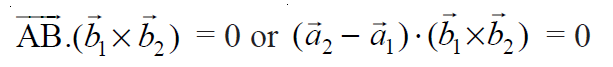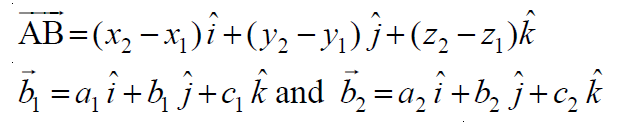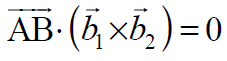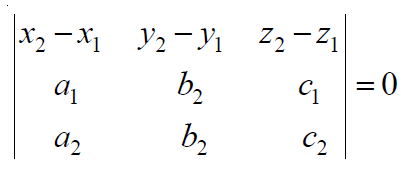Dadas dos líneas L1 y L2 , cada una de las cuales pasa por un punto cuyo vector de posición se da como (X, Y, Z) y son paralelas a la línea cuyas relaciones de dirección se dan como (a, b, c) , la tarea es verificar si la línea L1 y L2 son coplanares o no.
Coplanar: si dos líneas están en el mismo plano , entonces las líneas se pueden llamar coplanares.
Ejemplo:
Entrada:
L1: (x1, y1, z1) = (-3, 1, 5) y (a1, b1, c1) = (-3, 1, 5)
L2: (x1, y1, z1) = (-1 , 2, 5) y (a1, b1, c1) = (-1, 2, 5)
Salida: Las líneas son coplanaresEntrada:
L1: (x1, y1, z1) = (1, 2, 3) y (a1, b1, c1) = (2, 4, 6)
L2: (x1, y1, z1) = (-1, – 2, -3) y (a1, b1, c1) = (3, 4, 5)
Salida: Las líneas no son coplanares
Acercarse:
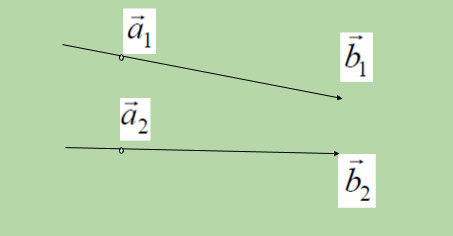
Hay dos formas de expresar una recta en 3 dimensiones:
Forma vectorial:
La ecuación de dos rectas cuya coplanaridad se va a determinar en forma vectorial .
En la ecuación anterior de una línea, un vector es un punto en el plano 3D desde el cual pasa una línea dada, llamado vector de posición a y b vector es la línea vectorial en el plano 3D a la que nuestra línea dada es paralela . Entonces se puede decir que la línea (1) pasa por el punto, digamos A , con el vector de posición a1 y es paralela al vector b1 y la línea (2) pasa por el punto, digamos B con el vector de posición a2 y es paralela a vector b2 . Por lo tanto:
Las líneas dadas son coplanares si y solo si el vector AB es perpendicular al producto vectorial de los vectores b1 y b2 , es decir,
Aquí, el producto cruzado de los vectores b1 y b2 dará otra línea vectorial que será perpendicular a las líneas vectoriales b1 y b2 . y AB es el vector línea que une los vectores de posición a1 y a2 de dos líneas dadas. Ahora, verifique si dos líneas son coplanares o no determinando que el producto escalar anterior es cero o no.
Forma cartesiana:
Sean (x1, y1, z1) y (x2, y2, z2) las coordenadas de los puntos A y B respectivamente.
Sean a1, b1, c1 y a2, b2, c2 las relaciones de dirección de los vectores b1 y b2 respectivamente. Después
Las rectas dadas son coplanares si y solo si:
En forma cartesiana se puede expresar como:
Por lo tanto, para ambos tipos de formas se necesita un vector de posición a1 y a2 en la entrada como (x1, y1, z1) y (x2, y2, z2) respectivamente y relaciones de dirección de los vectores b1 y b2 como (a1, b1, c1) y (a2, b2, c2) respectivamente.
Siga los pasos a continuación para resolver el problema:
- Inicialice una array de 3 X 3 para almacenar los elementos del Determinante que se muestra arriba.
- Calcule el producto vectorial de b2 y b1 y el producto escalar de (a2 – a1) .
- Si el valor del Determinante es 0, las líneas son coplanares. De lo contrario, son no coplanares.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program implement
// the above approach
#include <iostream>
using namespace std;
// Function to generate determinant
int det(int d[][3])
{
int Sum = d[0][0] * ((d[1][1] * d[2][2]) - (d[2][1] * d[1][2]));
Sum -= d[0][1] * ((d[1][0] * d[2][2]) - (d[1][2] * d[2][0]));
Sum += d[0][2] * ((d[0][1] * d[1][2]) -(d[0][2] * d[1][1]));
// Return the sum
return Sum;
}
// Driver Code
int main()
{
// Position vector of first line
int x1 = -3, y1 = 1, z1 = 5;
// Direction ratios of line to
// which first line is parallel
int a1 = -3, b1 = 1, c1 = 5;
// Position vectors of second line
int x2 = -1, y2 = 2, z2 = 5;
// Direction ratios of line to
// which second line is parallel
int a2 = -1, b2 = 2, c2 = 5;
// Determinant to check coplanarity
int det_list[3][3] = { {x2 - x1, y2 - y1, z2 - z1},
{a1, b1, c1}, {a2, b2, c2}};
// If determinant is zero
if(det(det_list) == 0)
{
cout << "Lines are coplanar" << endl;
}
// Otherwise
else
{
cout << "Lines are non coplanar" << endl;
}
return 0;
}
// This code is contributed by avanitrachhadiya2155
Java
// Java program implement
// the above approach
import java.io.*;
class GFG{
// Function to generate determinant
static int det(int[][] d)
{
int Sum = d[0][0] * ((d[1][1] * d[2][2]) -
(d[2][1] * d[1][2]));
Sum -= d[0][1] * ((d[1][0] * d[2][2]) -
(d[1][2] * d[2][0]));
Sum += d[0][2] * ((d[0][1] * d[1][2]) -
(d[0][2] * d[1][1]));
// Return the sum
return Sum;
}
// Driver Code
public static void main (String[] args)
{
// Position vector of first line
int x1 = -3, y1 = 1, z1 = 5;
// Direction ratios of line to
// which first line is parallel
int a1 = -3, b1 = 1, c1 = 5;
// Position vectors of second line
int x2 = -1, y2 = 2, z2 = 5;
// Direction ratios of line to
// which second line is parallel
int a2 = -1, b2 = 2, c2 = 5;
// Determinant to check coplanarity
int[][] det_list = { {x2 - x1, y2 - y1, z2 - z1},
{a1, b1, c1}, {a2, b2, c2}};
// If determinant is zero
if(det(det_list) == 0)
System.out.print("Lines are coplanar");
// Otherwise
else
System.out.print("Lines are non coplanar");
}
}
// This code is contributed by offbeat
Python3
# Python Program implement
# the above approach
# Function to generate determinant
def det(d):
Sum = d[0][0] * ((d[1][1] * d[2][2])
- (d[2][1] * d[1][2]))
Sum -= d[0][1] * ((d[1][0] * d[2][2])
- (d[1][2] * d[2][0]))
Sum += d[0][2] * ((d[0][1] * d[1][2])
- (d[0][2] * d[1][1]))
# Return the sum
return Sum
# Driver Code
if __name__ == '__main__':
# Position vector of first line
x1, y1, z1 = -3, 1, 5
# Direction ratios of line to
# which first line is parallel
a1, b1, c1 = -3, 1, 5
# Position vectors of second line
x2, y2, z2 = -1, 2, 5
# Direction ratios of line to
# which second line is parallel
a2, b2, c2 = -1, 2, 5
# Determinant to check coplanarity
det_list = [[x2-x1, y2-y1, z2-z1],
[a1, b1, c1], [a2, b2, c2]]
# If determinant is zero
if(det(det_list) == 0):
print("Lines are coplanar")
# Otherwise
else:
print("Lines are non coplanar")
C#
// C# program implement
// the above approach
using System;
class GFG{
// Function to generate determinant
static int det(int[,] d)
{
int Sum = d[0, 0] * ((d[1, 1] * d[2, 2]) -
(d[2, 1] * d[1, 2]));
Sum -= d[0, 1] * ((d[1, 0] * d[2, 2]) -
(d[1, 2] * d[2, 0]));
Sum += d[0, 2] * ((d[0, 1] * d[1, 2]) -
(d[0, 2] * d[1, 1]));
// Return the sum
return Sum;
}
// Driver Code
public static void Main()
{
// Position vector of first line
int x1 = -3, y1 = 1, z1 = 5;
// Direction ratios of line to
// which first line is parallel
int a1 = -3, b1 = 1, c1 = 5;
// Position vectors of second line
int x2 = -1, y2 = 2, z2 = 5;
// Direction ratios of line to
// which second line is parallel
int a2 = -1, b2 = 2, c2 = 5;
// Determinant to check coplanarity
int[,] det_list = { {x2 - x1, y2 - y1, z2 - z1},
{a1, b1, c1}, {a2, b2, c2}};
// If determinant is zero
if (det(det_list) == 0)
Console.Write("Lines are coplanar");
// Otherwise
else
Console.Write("Lines are non coplanar");
}
}
// This code is contributed by sanjoy_62
Javascript
<script>
// JavaScript program for the above approach
// Function to generate determinant
function det(d)
{
let Sum = d[0][0] * ((d[1][1] * d[2][2]) -
(d[2][1] * d[1][2]));
Sum -= d[0][1] * ((d[1][0] * d[2][2]) -
(d[1][2] * d[2][0]));
Sum += d[0][2] * ((d[0][1] * d[1][2]) -
(d[0][2] * d[1][1]));
// Return the sum
return Sum;
}
// Driver Code
// Position vector of first line
let x1 = -3, y1 = 1, z1 = 5;
// Direction ratios of line to
// which first line is parallel
let a1 = -3, b1 = 1, c1 = 5;
// Position vectors of second line
let x2 = -1, y2 = 2, z2 = 5;
// Direction ratios of line to
// which second line is parallel
let a2 = -1, b2 = 2, c2 = 5;
// Determinant to check coplanarity
let det_list = [[x2 - x1, y2 - y1, z2 - z1],
[a1, b1, c1], [a2, b2, c2]];
// If determinant is zero
if(det(det_list) == 0)
document.write("Lines are coplanar");
// Otherwise
else
document.write("Lines are non coplanar");
</script>
Lines are coplanar
Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por amit_mangal_ y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA