Encuentre el valor de cos 30°.

La trigonometría es la rama de las matemáticas que se ocupa de la relación de los lados con los ángulos en un triángulo. Con la trigonometría es posible averiguar las alturas de grandes montañas o torres, también en astronomía, se usa para encontrar la distancia entre estrellas o planetas y es muy utilizada en física, arquitectura y sistemas de navegación GPS. La trigonometría se basa en el principio de que “si dos triángulos tienen el mismo conjunto de ángulos, entonces sus lados están en la misma proporción”. La longitud de los lados puede ser diferente, pero las proporciones de los lados son las mismas.

Funciones trigonométricas

Las funciones trigonométricas también se llaman funciones circulares o razones trigonométricas. La relación de ángulos y lados está representada por estas funciones trigonométricas. Hay seis funciones trigonométricas Seno, Coseno, Tangente, Cosecante, Secante, Cotangente . Las representaciones de los lados para las seis razones son,

• sen A = Perpendicular / Hipotenusa
• cos A = Base / Hipotenusa
• tan A = Perpendicular / Base
• cuna A = Base / Perpendicular
• sec A = Hipotenusa / Base
• cosec A = Hipotenusa / Perpendicular.

Aquí, A es el ángulo opuesto al lado perpendicular. Aprendamos qué son la perpendicular, la base y la hipotenusa de un triángulo rectángulo,

1. Perpendicular: El lado frente al ángulo es perpendicular. En este caso, el lado frente a 30 grados se llama perpendicular.
2. Base: Una base es uno de los lados que toca un ángulo, pero la hipotenusa nunca puede ser considerada como base.
3. Hipotenusa: Es un lado opuesto a 90°. es el lado más grande.

Tenga en cuenta los cambios perpendiculares y de base a medida que cambia el ángulo. En un triángulo, un lado es perpendicular para un ángulo, pero el mismo lado es base para otro ángulo, pero la hipotenusa sigue siendo la misma porque es un lado opuesto al ángulo de 90°. 

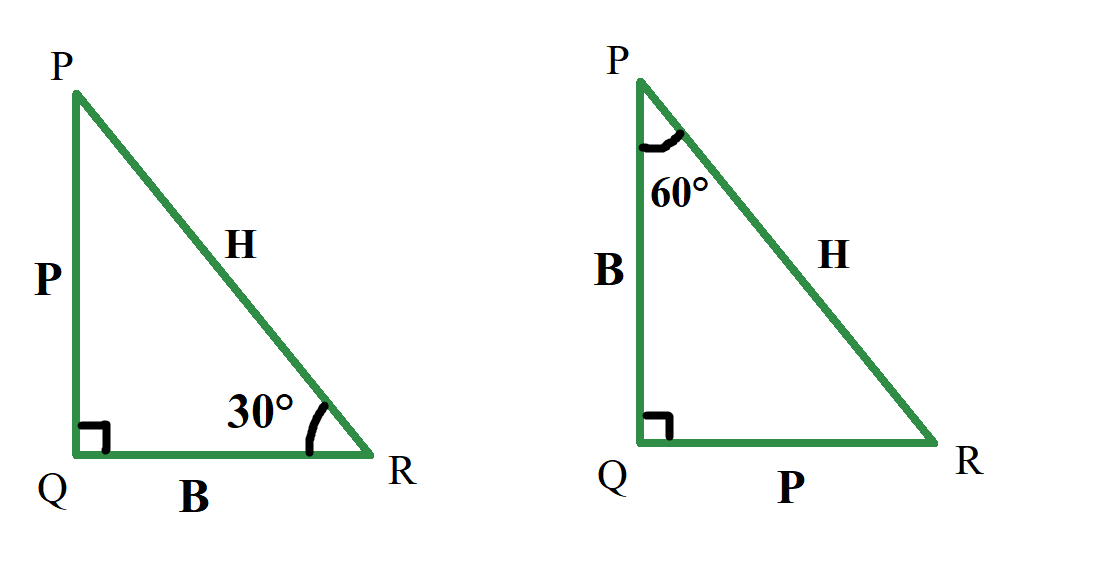
Como se muestra en el diagrama anterior para el mismo triángulo, si se considera un ángulo de 30°, la perpendicular es el lado PQ, pero si se considera un ángulo de 60°, la perpendicular es el lado QR.

Encuentre el valor de Cos 30°

Para calcular Cos 30° tomamos proporciones de su Base y su hipotenusa. para lo cual tenemos que calcular la longitud de Base e hipotenusa. Para encontrar las longitudes de los lados nos ayudamos de un triángulo equilátero. Un triángulo rectángulo que tiene 30° y 60° se obtiene dividiendo un triángulo equilátero en dos mitades por altura.

• Toma un triángulo equilátero de 2 m de lado.
• Ahora desde cualquier vértice dibuja una altitud.
• La altura dibujada divide el triángulo equilátero en dos triángulos rectángulos.
• Ahora tenemos una longitud de dos lados en el triángulo rectángulo.
• El tercer lado se calcula mediante el teorema de Baudhayan o el teorema de Pitágoras .

Es una propiedad de la Altitud en un triángulo equilátero que biseca el ángulo desde el cual se dibuja y biseca el lado opuesto en un ángulo recto.

Se obtiene un triángulo ADC que es un triángulo rectángulo y contiene un ángulo de 30° y 60°. El lado AC que es hipotenusa mide 2m y el lado DC mide 1m. Ahora calculamos la longitud del lado AD usando el teorema de Pitágoras. Sea x la longitud del lado AD. Aplicando el teorema de Pitágoras en el triángulo ADC.

P ² + B ² = H ²

DA ² + CC ² = CA ²

x ² + 1 ² = 2 ²

x2 + ¹ = 4

x2 = ³

X = √3

Cos 30° = AD/AC

coseno 30° = √3/2

Encuentra otras razones trigonométricas también,

sen 30° = 1/2

Tan 30° = 1/√3

Problemas de muestra

Pregunta 1: En un triángulo rectángulo, la base del ángulo de 30° es 9m. Encuentra la longitud de la hipotenusa.

Solución:

Dado: Base = 9m

Cos = √3/2

B/H = √3/2

9/H = √3/2 

H = (9 × 2) / √3

H=6√3m 

Pregunta 2: En un triángulo rectángulo, la hipotenusa mide 16m. y un ángulo mide 30°, halla los otros dos lados del triángulo .

Solución:

Dado, Hipotenusa = 16, ángulo = 30°

Cos 30 = B/H

B/H = √3/2

B/16 = √3/2

B = 8√3m

El tercer lado se calcula usando el teorema de Pitágoras.

P ² + B ² = H ²

PAG ² + (8√3) ² =1 6 ²

P2 ⁺  192 = 256

P2 ⁼   64

pag = 8m

Los lados del triángulo son – 8m, 8√3m, 16m.