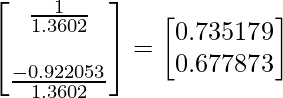¿Qué es PCA?
El principio rector principal para el análisis de componentes principales es la EXTRACCIÓN DE CARACTERÍSTICAS, es decir, «las características de un conjunto de datos deben ser menores, así como la similitud entre ellas es muy inferior». En PCA, se extrae un nuevo conjunto de características de las características originales que son de naturaleza bastante diferente. Entonces, un espacio de características n-dimensional se transforma en un espacio de características m-dimensional. , donde las dimensiones son ortogonales entre sí.
Concepto de ortogonalidad:
(Para entender este tema, tenemos que ir al concepto de espacio vectorial en álgebra lineal) El Espacio Vectorial es un conjunto de vectores. Se pueden representar como una combinación lineal del conjunto más pequeño de vectores llamados VECTORES BASE. Entonces, cualquier vector ‘v’ en un espacio vectorial se puede representar como:
![]()
donde a representa ‘n’ escalares y u representa los vectores base. Los vectores base son ortogonales entre sí. La ortogonalidad de los vectores se puede considerar como una extensión de los vectores que son perpendiculares en un espacio vectorial 2D . Entonces, nuestro vector de características (conjunto de datos) se puede transformar en un conjunto de componentes principales (al igual que los vectores base).
Objetivos de PCA:
- Las nuevas funciones son distintas, es decir, la covarianza entre las nuevas funciones (en el caso de PCA, son los componentes principales) es 0 .
- Los componentes principales se generan en orden de variabilidad en los datos que captura. Por lo tanto, el primer componente principal debe capturar la máxima variabilidad, el segundo debe capturar la siguiente variabilidad más alta, etc.
- La suma de la varianza de las nuevas características/los componentes principales debe ser igual a la suma de la varianza de las características originales.
Trabajo de PCA:
PCA funciona en un proceso llamado Descomposición de valores propios de una array de covarianza de un conjunto de datos. Los pasos son los siguientes:
- Primero, calcule la array de covarianza de un conjunto de datos.
- Luego, calcule los vectores propios de la array de covarianza.
- El vector propio que tiene el valor propio más alto representa la dirección en la que existe la varianza más alta. Así que esto ayudará a identificar el primer componente principal.
- El vector propio que tiene el siguiente valor propio más alto representa la dirección en la que los datos tienen la varianza restante más alta y también es ortogonal a la primera dirección. Entonces, esto ayuda a identificar el segundo componente principal.
- Así, identifique los vectores propios ‘k’ superiores que tienen valores propios ‘k’ superiores para obtener los componentes principales ‘k’.
Numérico para PCA:
Considere el siguiente conjunto de datos
| x1 | 2.5 | 0.5 | 2.2 | 1.9 | 3.1 | 2.3 | 2.0 | 1.0 | 1.5 | 1.1 |
| x2 | 2.4 | 0.7 | 2.9 | 2.2 | 3.0 | 2.7 | 1.6 | 1.1 | 1.6 | 0.9 |
Paso 1: estandarizar el conjunto de datos
Media para ![]() = 1.81 =
= 1.81 = ![]()
Media para ![]() = 1.91 =
= 1.91 = ![]()
Cambiaremos el conjunto de datos.
| 0,69 | -1.31 | 0.39 | 0.09 | 1.29 | 0.49 | 0.19 | -0.81 | -0.31 | -0.71 | |
| 0.49 | -1.21 | 0.99 | 0.29 | 1.09 | 0.79 | -0.31 | -0.81 | -0.31 | -1.01 |
Paso 2: encuentre los valores propios y los vectores propios
Array de correlación c = ![]()
donde, X es la Array del Conjunto de Datos (En este numérico, es una array de 10 X 2)
![]() is the transpose of the X (In this numerical, it is a 2 X 10 matrix) and N is the number of elements = 10
is the transpose of the X (In this numerical, it is a 2 X 10 matrix) and N is the number of elements = 10
Asi que, ![]()
{Entonces, para calcular la array de correlación, tenemos que hacer la multiplicación de la array del conjunto de datos con su transpuesta}
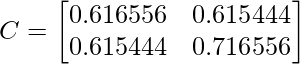
Usando la ecuación, | C- ![]() yo | = 0 – ecuación (i) donde { \lambda es el valor propio e I es la Array Identidad }
yo | = 0 – ecuación (i) donde { \lambda es el valor propio e I es la Array Identidad }
Entonces, resolviendo la ecuación (i)
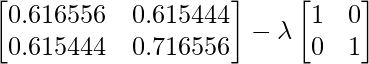
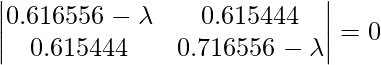
Tomando el determinante del lado izquierdo, obtenemos
![]()
![]()
Obtenemos dos valores para ![]() , que son (
, que son ( ![]() ) = 1.28403 y (
) = 1.28403 y ( ![]() ) = 0.0490834 . Ahora tenemos que encontrar los vectores propios para los valores propios
) = 0.0490834 . Ahora tenemos que encontrar los vectores propios para los valores propios ![]() y
y ![]()
Para encontrar los vectores propios a partir de los valores propios, utilizaremos el siguiente enfoque:
Primero, encontraremos los vectores propios para el valor propio 1.28403 usando la ecuación ![]()
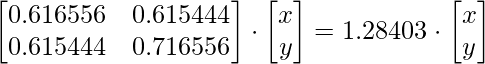
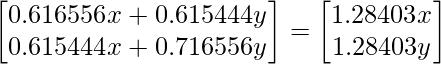
Resolviendo las arrays, obtenemos
0,616556x + 0,615444y = 1,28403x; x = 0.922049 y
(x e y pertenecen a la array X) por lo que si ponemos y = 1, x resulta ser 0,922049. Así que ahora la array X actualizada se verá así:
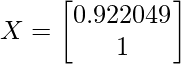
IMP: Hasta ahora no hemos llegado a los vectores propios, tenemos que hacer algunas modificaciones en la array X. Son los siguientes:
A. Encuentra la raíz cuadrada de la suma de los cuadrados del elemento en la array X, es decir
B. Ahora divide los elementos de la array X por el número 1.3602 (acabo de encontrar eso)

Así que ahora encontramos los vectores propios para el vector propio
, son 0.67787 y 0.73518
En segundo lugar, encontraremos los vectores propios para el valor propio 0.0490834 usando la ecuación {Mismo enfoque que en el paso anterior)
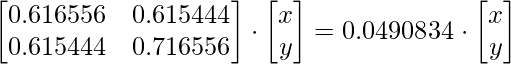
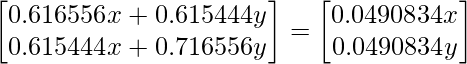
Resolviendo las arrays, obtenemos
0,616556x + 0,615444y = 0,0490834x; y = -0.922053
(x e y pertenecen a la array X) así que si ponemos x = 1, y resulta ser -0.922053 Así que ahora la array X actualizada se verá así:
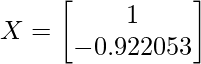
IMP: Hasta ahora no hemos llegado a los vectores propios, tenemos que hacer algunas modificaciones en la array X. Son los siguientes:
A. Encuentra la raíz cuadrada de la suma de los cuadrados de los elementos en la array X, es decir
B. Ahora divide los elementos de la array X por el número 1.3602 (acabo de encontrar eso)
Así que ahora encontramos los vectores propios para el vector propio \lambda_2, son 0.735176 y 0.677873
Suma de valores propios ( ![]() ) y (
) y ( ![]() ) = 1,28403 + 0,0490834 = 1,33 = Varianza total {La mayoría de la varianza proviene de
) = 1,28403 + 0,0490834 = 1,33 = Varianza total {La mayoría de la varianza proviene de ![]() }
}
Paso 3: Organizar valores propios
El vector propio con el valor propio más alto es el componente principal del conjunto de datos. Entonces, en este caso, los vectores propios de lambda1 son los componentes principales.
{Básicamente, para completar el número, solo tenemos que resolver hasta este paso, pero si tenemos que probar por qué hemos elegido ese vector propio en particular, tenemos que seguir los pasos del 4 al 6 }
Paso 4: Vector de características de formulario
 Este es el VECTOR DE CARACTERÍSTICAS para Numérico
Este es el VECTOR DE CARACTERÍSTICAS para Numérico
Donde la primera columna son los vectores propios de ![]() y la segunda columna son los vectores propios de
y la segunda columna son los vectores propios de ![]()
Paso 5: transformar el conjunto de datos original
Usa la ecuación Z = XV

Paso 6: Reconstrucción de datos
Use la ecuación X = ![]() (
( ![]() es la transposición de V), X = Fila de datos medios cero
es la transposición de V), X = Fila de datos medios cero

Entonces, para reconstruir los datos originales, seguimos:
Conjunto de datos original de la fila = Datos de la media cero de la fila + Media original

Entonces, para los vectores propios del primer valor propio, los datos se pueden reconstruir de manera similar al conjunto de datos original. Por lo tanto, podemos decir que el componente principal del conjunto de datos es 1.28403 seguido de 0.0490834 ![]()
![]()
Publicación traducida automáticamente
Artículo escrito por versatile1990 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA