En Machine Learning, a menudo lo que hacemos es recopilar datos, visualizarlos, luego ajustar una curva en el gráfico y luego predecir ciertos parámetros en función del ajuste de la curva. Si tenemos algunos datos teóricos, podemos usar el ajuste de curvas del conjunto de datos verificados para extraer la ecuación y verificarla. Entonces, para encontrar la ecuación de una curva de cualquier orden, ya sea lineal, cuadrática o polinomial, usamos ecuaciones diferenciales y luego, integrando esa ecuación, podemos obtener el ajuste de la curva.
En Python SciPy , este proceso se puede realizar fácilmente para resolver la ecuación diferencial al integrarla matemáticamente usando odeint(). La odeint(modelo, y0, t)se puede utilizar para resolver cualquier ecuación diferencial de orden tomando tres o más parámetros.
Parámetros:
modelo : la ecuación diferencial
y0 : valor inicial de Y
t : el espacio de tiempo para el que queremos la curva (básicamente, el rango de x)
Ilustremos esto con un ejemplo:
Código: Para resolver la ecuación para obtener y = x – 1 + 2 (e^-x) como la solución
python3
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Define a function which calculates the derivative by making dy/dx as
# the subject of formula in the given above equation
def dy_dx(y, x):
return x - y
#Here we define the graph limits for x
xs = np.linspace(-5,5,100)
#Initially y=1 given
y0 = 1.0
# This scipy.integrate.odeint() integrates the given equation by taking
# 3 parameters odeint(model,y0,t)
# model- the differential equation function
# y0-the initial value of y
# t- the timepoints for which we need to plot the curve
ys = odeint(dy_dx, y0, xs)
ys = np.array(ys).flatten()
# By using the matplotlib.pyplot library we plot the curve after integration
plt.rcParams.update({'font.size': 14}) # increase the font size
plt.xlabel("x-values")
plt.ylabel("Y- values")
plt.title('Curve of -> y=x-1+2*(e^-x)')
plt.plot(xs, ys,color='green')
Salida:
este es el gráfico generado mediante el uso de scipy.integrate.odeint() que se puede ver a continuación y se puede usar para el ajuste de curvas, para analizar los datos en el aprendizaje automático.
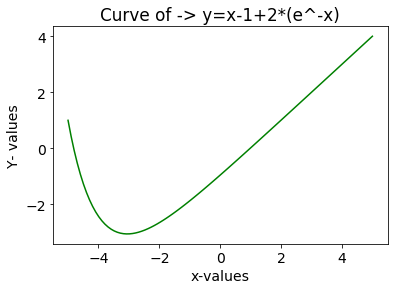
El gráfico generado después de integrar la ecuación diferencial
Publicación traducida automáticamente
Artículo escrito por dipesh99kumar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
