Una de las tareas principales involucradas en cualquier empresa de aprendizaje automático supervisado es seleccionar las mejores características del conjunto de datos dado para obtener los mejores resultados. Una forma de seleccionar estas características es la prueba Chi-Square.
Matemáticamente, se realiza una prueba de Chi-Cuadrado en dos distribuciones para determinar el nivel de similitud de sus respectivas varianzas. En su hipótesis nula , asume que las distribuciones dadas son independientes. Por lo tanto, esta prueba se puede utilizar para determinar las mejores características para un conjunto de datos dado al determinar las características de las que depende más la etiqueta de clase de salida. Para cada característica en el conjunto de datos, ![]() se calcula y luego se ordena en orden descendente según el
se calcula y luego se ordena en orden descendente según el ![]() valor. Cuanto mayor sea el valor de
valor. Cuanto mayor sea el valor de ![]() , más dependiente será la etiqueta de salida de la función y mayor será la importancia que tiene la función para determinar la salida.
, más dependiente será la etiqueta de salida de la función y mayor será la importancia que tiene la función para determinar la salida.
Deje que la característica en cuestión tenga m valores de atributo y que la salida tenga k etiquetas de clase. Entonces el valor de ![]() está dado por la siguiente expresión:-
está dado por la siguiente expresión:-
dónde
![]() – Observed frequency
– Observed frequency
![]() – Expected frequency
– Expected frequency
Para cada función, se crea una tabla de contingencia con m filas y k columnas. Cada celda (i,j) denota el número de filas que tienen la función de atributo como i y la etiqueta de clase como k. Por lo tanto, cada celda de esta tabla indica la frecuencia observada. Para calcular la frecuencia esperada para cada celda, primero se calcula la proporción del valor de la característica en el conjunto de datos total y luego se multiplica por el número total de la etiqueta de clase actual.
Ejemplo resuelto:
Considere la siguiente tabla: –
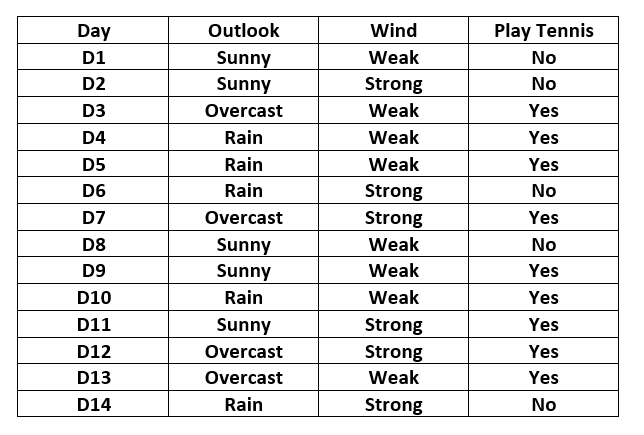
Aquí, la variable de salida es la columna denominada «PlayTennis» que determina si se jugó tenis en el día dado dadas las condiciones climáticas.
La tabla de contingencia para la función «Outlook» se construye de la siguiente manera: –
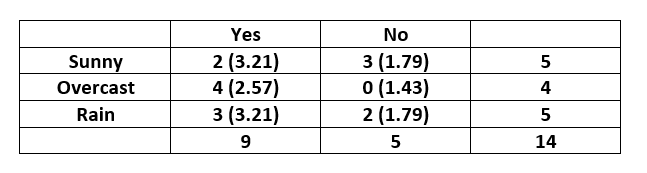
Tenga en cuenta que el valor esperado para cada celda se da entre paréntesis.
El valor esperado para la celda (Soleado, Sí) se calcula como ![]() y de manera similar para los demás.
y de manera similar para los demás.
El ![]() valor se calcula de la siguiente manera: –
valor se calcula de la siguiente manera: –
![]()
![]()
La tabla de contingencia para la función «Viento» se construye de la siguiente manera:
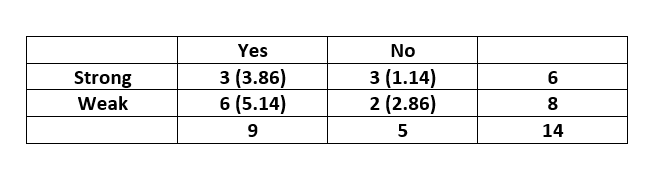
El ![]() valor se calcula de la siguiente manera: –
valor se calcula de la siguiente manera: –
![]()
![]()
Al comparar las dos puntuaciones, podemos concluir que la función «Viento» es más importante para determinar la salida que la función «Perspectiva».
Este artículo demuestra cómo hacer una selección de características utilizando la prueba Chi-Square.
Publicación traducida automáticamente
Artículo escrito por AlindGupta y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA