ML | ¿Por qué regresión logística en la clasificación?

Usando la Regresión Lineal, todas las predicciones >= 0.5 se pueden considerar como 1 y el resto < 0.5 se puede considerar como 0. Pero entonces surge la pregunta de por qué no se puede realizar la clasificación usándola.

Problema –

Supongamos que estamos clasificando un correo como spam o no spam y nuestro resultado es y , puede ser 0 (spam) o 1 (no spam). En el caso de la regresión lineal, h _θ (x) puede ser > 1 o < 0. Aunque nuestra predicción debería estar entre 0 y 1, el modelo predecirá un valor fuera del rango, es decir, quizás > 1 o < 0.

Entonces, es por eso que para una tarea de clasificación, la regresión logística/sigmoidea juega su papel.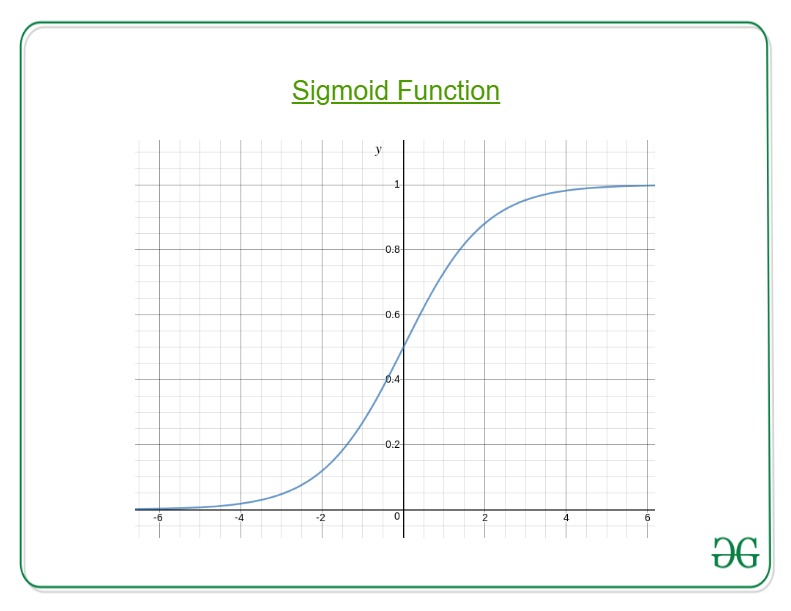

$h_{\Theta} (x) = g (\Theta ^{T}x) z = \Theta ^{T}x g(z) = \frac{1}{1+e^{-z}}$

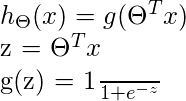
Aquí, reemplazamos θ ^T x en la función logística donde θ son los pesos/parámetros y x es la entrada y h _θ (x) es la función de hipótesis. g() es la función sigmoidea.

$h_{\Theta} (x) = P( y =1 | x ; \Theta )$

Significa que y = 1 probabilidad cuando x está parametrizado a θ

Para obtener los valores discretos 0 o 1 para la clasificación, se definen límites discretos. La función de hipótesis se puede traducir como

$h_{\Theta} (x) \geq 0.5 \rightarrow y = 1 h_{\Theta} (x) < 0.5 \rightarrow y = 0$

${g(z) \geq 0.5} \\ {\Rightarrow \Theta ^{T}x \geq 0.5} \\ {\Rightarrow z \geq 0.5 }$

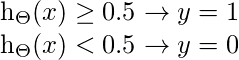
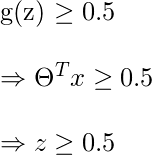
Límite de decisión es la línea que distingue el área donde y=0 y donde y=1. Estos límites de decisión resultan de la función de hipótesis bajo consideración.

Comprender el límite de decisión con un ejemplo:
dejemos que nuestra función de hipótesis sea

$h_{\Theta}(x)= g[\Theta_{0}+ \Theta_1x_1+\Theta_2x_2+ \Theta_3x_1^2 + \Theta_4x_2^2 ]$

Luego, el límite de decisión se parece a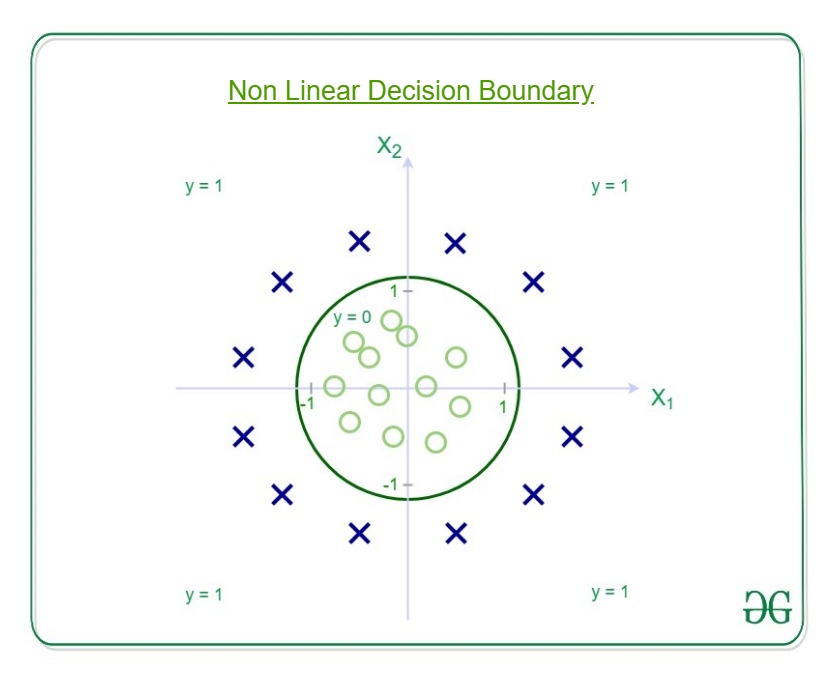

Deje que los pesos o los parámetros sean:

$\Theta=\begin{bmatrix} -1\\ 0\\ 0\\ 1\\ 1 \end{bmatrix}$

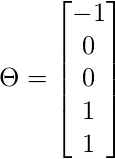
Entonces, predice y = 1 si

$-1 + x_{1}^2 + x_{2}^2 \geqslant 0$

$\Rightarrow x_{1}^2 + x_{2}^2 \geqslant 1$

Y esa es la ecuación de un círculo con radio = 1 y origen como centro. Este es el límite de decisión para nuestra hipótesis definida.

Publicación traducida automáticamente

Artículo escrito por Mohit Gupta_OMG 🙂 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta