Optimización Multivariada – Gradiente y Hessian

En un problema de optimización multivariante, existen múltiples variables que actúan como variables de decisión en el problema de optimización.
z = f(x ₁ , x ₂ , x ₃ … ..x norte ₎

Entonces, cuando observa este tipo de problemas, una función general z podría ser una función no lineal de las variables de decisión x ₁ , x ₂ , x ₃ a x _n . Entonces, hay n variables que uno podría manipular o elegir para optimizar esta función z. Tenga en cuenta que uno podría explicar la optimización univariante usando imágenes en dos dimensiones porque en la dirección x teníamos el valor de la variable de decisión y en la dirección y teníamos el valor de la función. Sin embargo, si se trata de optimización multivariante, entonces tenemos que usar imágenes en tres dimensiones y si las variables de decisión son más de 2, entonces es difícil de visualizar.

Gradiente:
antes de explicar el gradiente, contrastemos con la condición necesaria del caso univariado. Entonces, en caso de optimización univariada, la condición necesaria para que x sea el minimizador de la función f(x) es:
Condición necesaria de primer orden: f'(x) = 0

Entonces, la derivada en un caso unidimensional se convierte en lo que llamamos un gradiente en el caso multivariado.

De acuerdo con la condición necesaria de primer orden en la optimización univariada, por ejemplo, f'(x) = 0 o también se puede escribir como df/dx . Sin embargo, como hay muchas variables en el caso de multivariante y tenemos muchas derivadas parciales y el gradiente de la función f es un vector tal que en cada componente se puede calcular la derivada de la función con respecto a la variable correspondiente. Entonces, por ejemplo, $\parcial f/ \parcial x_1$ es el primer componente, $\parcial f/ \parcial x_2$ es el segundo componente y $\parcial f/ \parcial x_n$ es el último componente.
$Gradiente = \nabla f = \begin{bmatrix} \parcial f/ \parcial x_1\\ \parcial f/ \parcial x_2\\ ...\\ ...\\ \parcial f/ \parcial x_n\\ \end {barray}$

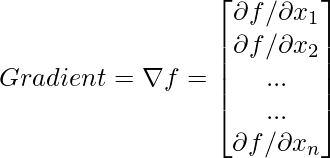
Nota: El gradiente de una función en un punto es ortogonal a los contornos .

Hessiana :
Del mismo modo, en el caso de optimización univariada, la condición suficiente para que x sea el minimizador de la función f(x) es:
Condición de suficiencia de segundo orden: f”(x) > 0 o d ² f/dx ² > 0

Y esto se reemplaza por lo que llamamos una array hessiana en el caso multivariante. Entonces, esta es una array de dimensión n*n, y el primer componente es $\parcial ^2f/ \parcial x_1^2$ , el segundo componente es $\parcial ^2f/\parcial x_1 \parcial x_2$ y así sucesivamente.

$Hessian = \nabla ^2 f = \begin{bmatrix} \partial ^2f/ \partial x_1^2 & \partial ^2f/\partial x_1 \partial x_2 & ... & \partial ^2f/ \partial x_1 \partial x_n\\ \partial ^2f/\partial x_2 \partial x_1 & \partial ^2f/ \partial x_2^2 & ... & \partial ^2f/ \partial x_2 \partial x_n\\ ... & ... & ... & ...\\ ... & ... & ... & ...\\ \partial ^2f/\partial x_n \partial x_1 & \partial ^2f/\partial x_n \partial x_2 & ... & \partial ^2f/ \partial x_n^2\\ \end{bmatrix}$

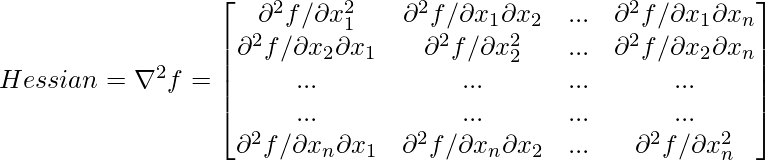
Nota:

Hessian es una array simétrica.

Se dice que la array hessiana es definida positiva en un punto si todos los valores propios de la array hessiana son positivos.

Publicación traducida automáticamente

Artículo escrito por AmiyaRanjanRout y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta