Dado un conjunto de dos variables aleatorias, encuentre la covarianza. La covarianza es una medida de cuánto varían juntas dos variables aleatorias. Es similar a la varianza, pero donde la varianza te dice cómo varía una sola variable, la covarianza te dice cómo varían dos variables juntas. La covarianza se puede calcular usando la fórmula 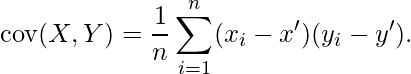
Donde x’ y y’ son las medias de dos conjuntos dados.
Ejemplos:
Input : arr1[] = {65.21, 64.75, 65.26, 65.76, 65.96}
arr2[] = {67.25, 66.39, 66.12, 65.70, 66.64}
Output : -0.0580511
Input : arr1[] = {5, 20, 40, 80, 100}
arr2[] = {10, 24, 33, 54, 10}
Output : 187.75
C++
// C++ Program to find covariance of two set.
#include <bits/stdc++.h>
using namespace std;
// Function to find mean.
float mean(float arr[], int n)
{
float sum = 0;
for (int i = 0; i < n; i++)
sum = sum + arr[i];
return sum / n;
}
// Function to find covariance.
float covariance(float arr1[], float arr2[], int n)
{
float sum = 0;
float mean_arr1 = mean(arr1, n);
float mean_arr2 = mean(arr2, n);
for (int i = 0; i < n; i++)
sum = sum + (arr1[i] - mean_arr1) * (arr2[i] - mean_arr2);
return sum / (n - 1);
}
// Driver function.
int main()
{
float arr1[] = { 65.21, 64.75, 65.26, 65.76, 65.96 };
int n = sizeof(arr1) / sizeof(arr1[0]);
float arr2[] = { 67.25, 66.39, 66.12, 65.70, 66.64 };
int m = sizeof(arr2) / sizeof(arr2[0]);
if (m == n)
cout << covariance(arr1, arr2, m);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
C
// C Program to find covariance of two set.
#include <stdio.h>
// Function to find mean.
float mean(float arr[], int n)
{
float sum = 0;
for (int i = 0; i < n; i++)
sum = sum + arr[i];
return sum / n;
}
// Function to find covariance.
float covariance(float arr1[], float arr2[], int n)
{
float sum = 0;
float mean_arr1 = mean(arr1, n);
float mean_arr2 = mean(arr2, n);
for (int i = 0; i < n; i++)
sum = sum + (arr1[i] - mean_arr1) * (arr2[i] - mean_arr2);
return sum / (n - 1);
}
// Driver function.
int main()
{
float arr1[] = { 65.21, 64.75, 65.26, 65.76, 65.96 };
int n = sizeof(arr1) / sizeof(arr1[0]);
float arr2[] = { 67.25, 66.39, 66.12, 65.70, 66.64 };
int m = sizeof(arr2) / sizeof(arr2[0]);
if (m == n)
printf("%f", covariance(arr1, arr2, m));
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
Java
// Java Program to find covariance of two set.
import java.io.*;
class GFG {
// Function to find mean.
static float mean(float arr[], int n)
{
float sum = 0;
for (int i = 0; i < n; i++)
sum = sum + arr[i];
return sum / n;
}
// Function to find covariance.
static float covariance(float arr1[], float arr2[], int n)
{
float sum = 0;
float mean_arr1 = mean(arr1, n);
float mean_arr2 = mean(arr2, n);
for (int i = 0; i < n; i++)
sum = sum + (arr1[i] - mean_arr1) * (arr2[i] - mean_arr2);
return sum / (n - 1);
}
// Driver code
public static void main(String[] args)
{
float arr1[] = { 65.21f, 64.75f, 65.26f, 65.76f, 65.96f };
int n = arr1.length;
float arr2[] = { 67.25f, 66.39f, 66.12f, 65.70f, 66.64f };
int m = arr2.length;
if (m == n)
System.out.println(covariance(arr1, arr2, m));
}
}
// This code is contributed by Aditya Kumar (adityakumar129)
Python3
# Python3 Program to find # covariance of two set. import math # Function to find mean. def mean(arr, n): sum = 0 for i in range(0, n): sum = sum + arr[i] return sum / n # Function to find covariance. def covariance(arr1, arr2, n): sum = 0 mean_arr1 = mean(arr1, n) mean_arr2 = mean(arr2, n) for i in range(0, n): sum = (sum + (arr1[i] - mean_arr1) * (arr2[i] - mean_arr2)) return sum / (n - 1) # Driver method arr1 = [65.21, 64.75, 65.26, 65.76, 65.96] n = len(arr1) arr2 = [67.25, 66.39, 66.12, 65.70, 66.64] m = len(arr2) if (m == n): print(covariance(arr1, arr2, m)) # This code is contributed by Aditya Kumar (adityakumar129)
C#
// C# Program to find
// covariance of two set.
using System;
class GFG {
// Function to find mean.
static float mean(float []arr, int n)
{
float sum = 0;
for(int i = 0; i < n; i++)
sum = sum + arr[i];
return sum / n;
}
// Function to find covariance.
static float covariance(float []arr1,
float []arr2, int n)
{
float sum = 0;
float mean_arr1 = mean(arr1,n);
float mean_arr2 = mean(arr2,n);
for(int i = 0; i < n; i++)
sum = sum + (arr1[i] - mean_arr1) *
(arr2[i] - mean_arr2);
return sum / (n - 1);
}
// Driver code
public static void Main () {
float []arr1 = {65.21f, 64.75f,
65.26f, 65.76f, 65.96f};
int n = arr1.Length;
float []arr2 = {67.25f, 66.39f,
66.12f, 65.70f, 66.64f};
int m = arr2.Length;
if (m == n)
Console.WriteLine(covariance(arr1, arr2, m));
}
}
// This code is contributed by vt_m.
PHP
<?php
// PHP Program to find
// covariance of two set.
// Function to find mean.
function mean( $arr, $n)
{
$sum = 0;
for( $i = 0; $i < $n; $i++)
$sum = $sum + $arr[$i];
return $sum / $n;
}
// Function to find covariance.
function covariance( $arr1, $arr2, $n)
{
$sum = 0;
$mean_arr1 = mean($arr1,$n);
$mean_arr2 = mean($arr2,$n);
for( $i = 0; $i < $n; $i++)
$sum = $sum + ($arr1[$i] -
$mean_arr1) *
($arr2[$i] -
$mean_arr2);
return $sum / ($n - 1);
}
// Driver function.
$arr1 = array(65.21, 64.75, 65.26,
65.76, 65.96);
$n = count($arr1);
$arr2 = array(67.25, 66.39, 66.12,
65.70, 66.64);
$m =count($arr2);
if ($m == $n)
echo covariance($arr1, $arr2, $m);
// This code is contributed by anuj_67.
?>
Javascript
<script>
// Javascript program to find
// covariance of two set.
// Function to find mean.
function mean(arr, n)
{
let sum = 0;
for(let i = 0; i < n; i++)
sum = sum + arr[i];
return sum / n;
}
// Function to find covariance.
function covariance(arr1, arr2, n)
{
let sum = 0;
let mean_arr1 = mean(arr1, n);
let mean_arr2 = mean(arr2, n);
for(let i = 0; i < n; i++)
sum = sum + (arr1[i] - mean_arr1) *
(arr2[i] - mean_arr2);
return sum / (n - 1);
}
// Driver code
let arr1 = [ 65.21, 64.75, 65.26, 65.76, 65.96 ];
let n = arr1.length;
let arr2 = [ 67.25, 66.39, 66.12, 65.70, 66.64 ];
let m = arr2.length;
if (m == n)
document.write(covariance(arr1, arr2, m));
// This code is contributed by souravmahato348
</script>
Producción:
-0.0580511
Complejidad temporal: O(N)
Espacio auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por Dharmendra_Kumar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA