En términos matemáticos, la secuencia Fn de los números de Fibonacci está definida por la relación de recurrencia
Fn = Fn-1 + Fn-2
Con valores semilla
F0 = 0 and F1 = 1.
Método 1 (usar recursividad):
Python3
# Function for nth Fibonacci number
def Fibonacci(n):
if n<= 0:
print("Incorrect input")
# First Fibonacci number is 0
elif n == 1:
return 0
# Second Fibonacci number is 1
elif n == 2:
return 1
else:
return Fibonacci(n-1)+Fibonacci(n-2)
# Driver Program
print(Fibonacci(10))
# This code is contributed by Saket Modi
34
Método 2 (usar programación dinámica):
Python3
# Function for nth fibonacci number - Dynamic Programming
# Taking 1st two fibonacci numbers as 0 and 1
FibArray = [0, 1]
def fibonacci(n):
if n<0:
print("Incorrect input")
elif n<= len(FibArray):
return FibArray[n-1]
else:
temp_fib = fibonacci(n-1)+fibonacci(n-2)
FibArray.append(temp_fib)
return temp_fib
# Driver Program
print(fibonacci(9))
# This code is contributed by Saket Modi
21
Producción:
21
Método 3 (Usar Programación Dinámica con Optimización de Espacio):
Python3
# Function for nth fibonacci number - Space Optimisation
# Taking 1st two fibonacci numbers as 0 and 1
def fibonacci(n):
a = 0
b = 1
if n < 0:
print("Incorrect input")
elif n == 0:
return a
elif n == 1:
return b
else:
for i in range(2, n):
c = a + b
a = b
b = c
return b
# Driver Program
print(fibonacci(9))
# This code is contributed by Saket Modi
21
Producción:
21
Método 4 (usando arreglos):
Python3
# creating an array in the function to find the nth number in fibonacci series. [0, 1, 1, ...] def fibonacci (n): if n<= 0: return "Incorrect Output" data = [0, 1] if n > 2: for i in range (2, n): data.append(data[i-1] + data[i-2]) return data[n-1] # Driver Program print(fibonacci(9)) # This Code is contributed by Prasun Parate (prasun_parate)
Producción :
144
Explicación:
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144]
Como sabemos que la serie de Fibonacci es la suma de los dos términos anteriores, entonces si ingresamos 12 como el entrada en el programa, por lo que deberíamos obtener 144 como salida. Y ese es el resultado.
Método 5 (usando la fórmula directa):
La fórmula para encontrar el n-ésimo número de Fibonacci es la siguiente:
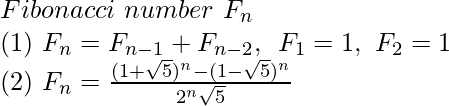
Python3
# To find the n-th Fibonacci Number using formula from math import sqrt # import square-root method from math library def nthFib(n): res = (((1+sqrt(5))**n)-((1-sqrt(5)))**n)/(2**n*sqrt(5)) # compute the n-th fibonacci number print(int(res),'is',str(n)+'th fibonacci number') # format and print the number # driver code nthFib(12) # This code is contributed by Kush Mehta
144 is 12th fibonacci number
¡ Consulte el artículo completo sobre Programa para números de Fibonacci para obtener más detalles!
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA