¿Número esperado de lanzamientos de monedas para obtener dos caras seguidas?

Problema : encontrar el número esperado de veces que se debe lanzar una moneda para obtener dos caras consecutivamente.

Solución : La clave es observar que si vemos cruz en el primer lanzamiento, básicamente arruina cualquier racha y por lo tanto tenemos que empezar de nuevo. En otras palabras, las primeras cruces hacen que todos los lanzamientos anteriores sean «desperdiciados» y eso aumenta el tiempo esperado condicional en ese número de lanzamientos.

Deje que el número esperado de lanzamientos de monedas sea . Ahora, hay tres casos posibles que se enumeran a continuación:

1. Si sale cruz en el primer lanzamiento de la moneda . Si en la primera tirada sale cruz significa que hemos desperdiciado una tirada y tendremos que hacer 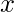más tiradas para alcanzar nuestro objetivo. La probabilidad de este evento es 1/2 y el número total de lanzamientos requeridos ahora será x+1 .
2. Si aparece cara en el primer lanzamiento de la moneda y cruz en el segundo lanzamiento . En este caso significa que hemos desperdiciado dos volteretas y tendremos que hacer 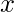más volteretas para llegar a nuestro objetivo. Por lo tanto, el número total de lanzamientos requeridos ahora será x+2 y la probabilidad de este evento es 1/4.
3. El último caso es si obtenemos dos caras consecutivas en dos lanzamientos consecutivos de la moneda respectivamente. La probabilidad de este evento es 1/4 y el número total de lanzamientos requeridos será 2.

Enmarcando los tres casos anteriores en forma de ecuaciones y sumando obtendremos:

x = (1/2)(x+1) + (1/4)(x+2) + (1/4)2
x = 1/2 [ (1+x) + 1/2(2+x) + 1 ]
x = 1/2 [ 1 + x + 1 + x/2 + 1 ]
x / 4 = 3/2
x = 6

Por lo tanto, x = 6 .

Por lo tanto, el número esperado de lanzamientos de moneda para obtener dos caras consecutivas es 6.