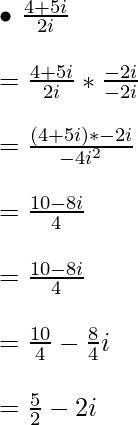Un número complejo es un número que se puede expresar de la forma a + bi , donde a y b son números reales e i representa la unidad imaginaria, satisfaciendo la ecuación i² = −1 . Por ejemplo, 5+6i es un número complejo, donde 5 es un número real y 6i es un número imaginario. Por lo tanto, la combinación del número real y el número imaginario es un número complejo. Puede haber cuatro tipos de operaciones algebraicas en números complejos que se mencionan a continuación. Las cuatro operaciones en los números complejos incluyen:
- Suma
- Sustracción
- Multiplicación
- División
Adición de Números Complejos
Para sumar dos números complejos, basta con sumar las partes real e imaginaria correspondientes.
(a + bi) + (c + di) = (a + c) + (b + d)i
Ejemplos:
- (7 + 8i) + (6 + 3i) = (7 + 6) + (8 + 3)i = 13 + 11i
- (2 + 5i) + (13 + 7i) = (2 + 13) + (7 + 5)i = 15 + 12i
- (-3 – 6i) + (-4 + 14i) = (-3 – 4) + (-6 + 14)i = -7 + 8i
- (4 – 3i) + (6 + 3i) = (4+6) + (-3+3)i = 10
- (6 + 11i) + (4 + 3i) = (4 + 6) + (11 + 3)i = 10 + 14i
Resta de Números Complejos
Para restar dos números complejos, simplemente resta las partes reales e imaginarias correspondientes.
(a + bi) − (c + di) = (a − c) + (b − d)i
Ejemplos:
- (6 + 8i) – (3 + 4i) = (6 – 3) + (8 – 4)i = 3 + 4i
- (7 + 15i) – (2 + 5i) = (7 – 2) + (15 – 5)i = 5 + 10i
- (-3 + 5i) – (6 + 9i) = (-3 – 6) + (5 – 9)i = -9 – 4i
- (14 – 3i) – (-7 + 2i) = (14 – (-7)) + (-3 – 2)i = 21 – 5i
- (-2 + 6i) – (4 + 13i) = (-2 – 4) + (6 – 13)i = -6 – 7i
Multiplicación de dos números complejos
La multiplicación de dos números complejos es lo mismo que la multiplicación de dos binomios. Supongamos que tenemos que multiplicar a + bi y c + di. Los multiplicaremos término a término.
(a + bi) ∗ (c + di) = (a + bi) ∗ c + (a + bi) ∗ di
= (a ∗ c + (b ∗ c)i)+((a ∗ d)i + b ∗ re ∗ −1)
= (un ∗ do – segundo ∗ re + yo(segundo ∗ do + un ∗ re))
Ejemplo 1 : Multiplica (1 + 4i) y (3 + 5i).
(1 + 4i) ∗ (3 + 5i) = (3 + 12i) + (5i + 20i 2 )
= 3 + 17i − 20
= −17 + 17i
Nota: La multiplicación de números complejos con números reales o puramente imaginarios se puede hacer de la misma manera.
Ejemplo 2: Multiplica 5 y (4 + 7i).
5 ∗ (4+7i) puede verse como (5 + 0i) ∗ (4 + 7i)
= 5 ∗ (4 + 7i)
= 20 + 35i
Ejemplo 3: Multiplica 3i y (2 + 6i).
3i ∗ (2 + 6i) puede verse como (0 + 3i) ∗ (2 + 6i)
= 3i ∗ (2 + 6i)
= 6i + 18i 2
= 6i − 18
= −18 + 6i
Ejemplo 4: Multiplica (5 + 3i) y (3 + 4i).
(5+3i) ∗ (3+4i) = (5 + 3i) ∗ 3 + (5 + 3i) ∗ 4i
= (15 + 9i) + (20i + 12i 2 )
= (15 − 12) + (20 + 9)i
= 3 + 29i
Repaso de Suma, Resta y Multiplicación de Números Complejos
- (a + bi) + (c + di) = (a + c) + (b + d)i
- (a + bi) − (c + di) = (a − c) + (b − d)i
- (a + bi) ∗ (c + di) = ((a ∗ c − b ∗ d) + (b ∗ c + a ∗ d)i)
Conjugado de un número complejo
En dos números complejos cualesquiera, si solo difiere el signo de la parte imaginaria, se conocen como un conjugado complejo entre sí. Así, el conjugado de un número complejo a + bi sería a – bi.
![]()
¿De qué sirve un complejo conjugado?

Así podemos observar que multiplicar un número complejo por su conjugado nos da un número real. Por tanto, la división de números complejos es posible multiplicando tanto el numerador como el denominador con el complejo conjugado del denominador.
Ejemplos de conjugados complejos
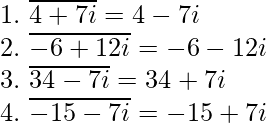
Propiedades de los conjugados complejos
Propiedad 1:
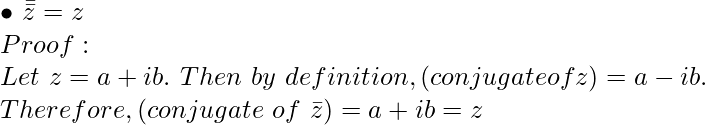
Propiedad 2:
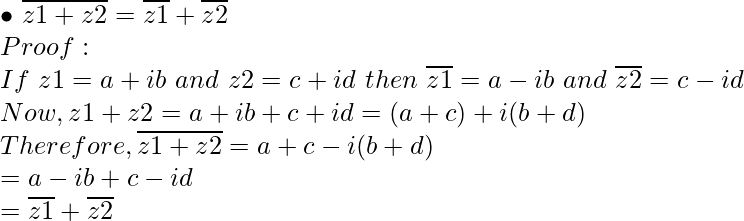
Propiedad 3:
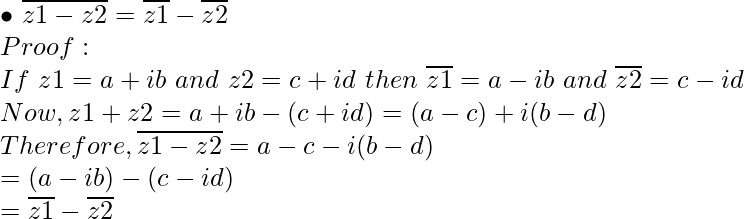
Propiedad 4:

Propiedad 5:
![Rendered by QuickLaTeX.com { \bullet } \ \overline {(\frac{z1}{z2})} = \frac{\overline {z1}}{\overline {z2}} ,\ provided\ z2\neq 0 \\ Proof: \\ According\ to\ the\ problem \\ z2 ≠ 0 ⇒ \overline {z2} ≠ 0 \\ Let, \frac{z1}{z2} = z3 \\ z1 = z2*z3 \\ ⇒ \overline {z1} = \overline {z2*z3} \\ ⇒ \overline {z1} = \overline {z2}*\overline {z3} \\ ⇒ \frac{\overline {z1}}{\overline {z2}} = \overline {z3} \\ \ \\ ⇒ \overline {(\frac{z1}{z2})} = \frac{\overline {z1}}{\overline {z2}}, [Since\ z3 = \frac{z1}{z2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4c84d4206ce9e918f0ec787e778a715c_l3.png)
División de dos números complejos
La división de números complejos se realiza multiplicando el numerador y el denominador por el complejo conjugado del denominador.

Ejemplo 1:

Ejemplo 2:
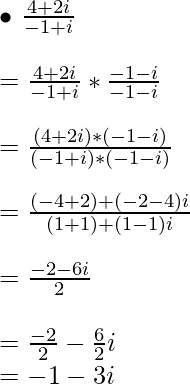
Ejemplo 3:
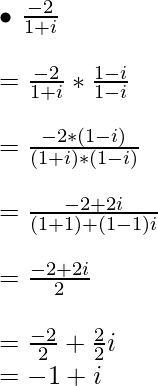
Ejemplo 4: