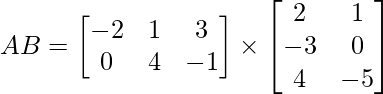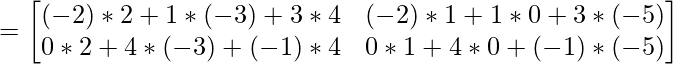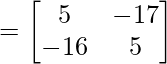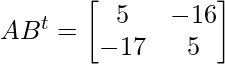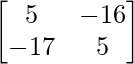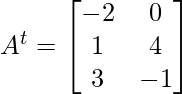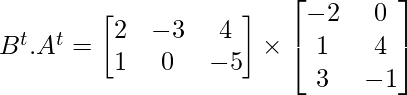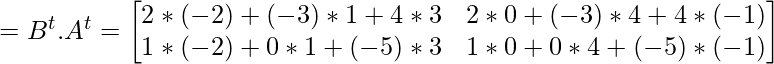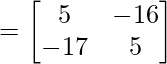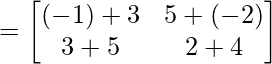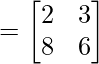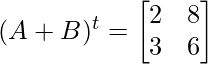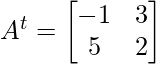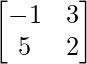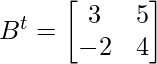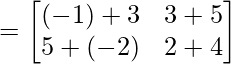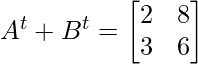El conocimiento de arrays es necesario para diversas ramas de las matemáticas. Las arrays son una de las herramientas más poderosas de las matemáticas. Ahora vea una de las características de la array en este artículo.
Transpuesta de una array
Esta es una de las principales propiedades de la array. El significado de transposición es intercambiar lugares de dos o más cosas. En el caso de la array, transponer significado cambia el índice de los elementos. En este caso, intercambiamos el elemento fila con el elemento columna o viceversa.
Sea A una array de tamaño m × n y A t es la traspuesta de la array A,
donde [a(ij)] de A = [a(ji)] de A t , aquí 1 ≤ i ≤ m y 1 ≤ j ≤ norte
Ejemplo:
Sea, el tamaño de la array A es 2 × 3 ,
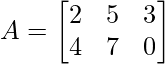
Por lo tanto,
Transpuesta de A o
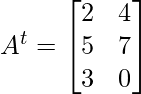
Después de transponer se convierte en 3 × 2
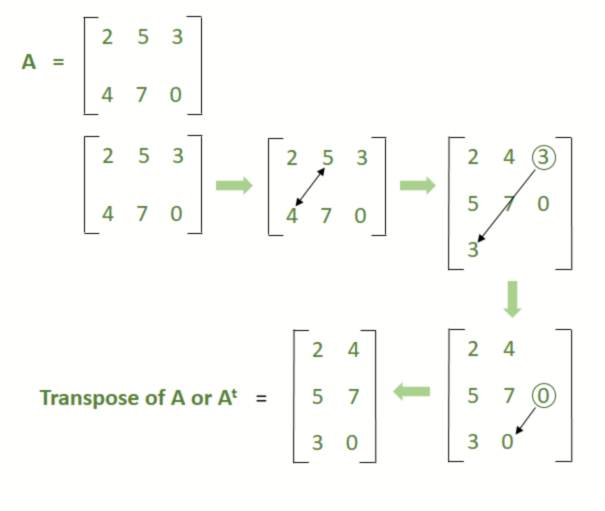
Propiedades de la transposición
Transpuesta de Producto de Arrays
Esta propiedad dice que, (AB) t = B t A t
Prueba
Aquí A y B son dos arrays de tamaño m × n y n × p respectivamente
y At y Bt son su forma transpuesta de tamaño n × m y p × n respectivamente (de la regla del producto de arrays).
Implica, si A = [a(ij)], y At = [c(ji)]
Entonces, [c(ji)] = [a(ij)]
y,
Si B = [b(jk)], y Bt = [d(kj)]
Entonces, [d(kj)] = [b(jk)]
Ahora, a partir de la regla del producto de arrays podemos escribir,
AB es la array m × p y (AB)t es la array p × m.
Además, Bt es una array ap × n y At es una array × m.
Esto implica que,
(Bt)(At) es una array ap × m.
Por lo tanto,
(AB)t y (Bt)(At) son ambas arrays p × m.
Ahora podemos escribir,
(k, i)ésimo elemento de (AB)t = (i, k)ésimo elemento de AB
(k, i)ésimo elemento de (B t )(A t )
Por lo tanto,
los elementos de (AB) t y (B t )(A t ) son iguales.
Por lo tanto,
(AB) t = (B t )(A t )
Ejemplo:
Dejar,
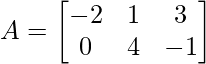
y
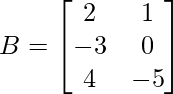
Demuestre que para estas arrays, (AB) t = (B t )(A t )
Solución:
Aquí A y B son arrays de 2 × 3 y 3 × 2 respectivamente. Entonces, por la regla del producto de una array, podemos encontrar su producto
y las arrays finales serían de array 2 × 2 .Encuentra LHS –
Ahora,
Entonces, Transponer de AB o
Encuentre RHS –
y
Asi que,
Por lo tanto,
(AB) t = B t .A t
Transpuesta de Adición de Arrays
Esta propiedad dice que (A + B) t = A t + B t
Demostrar:
Aquí A y B son dos arrays de tamaño m × n
Sean A = [a(ij)] y B = [b(ij)] de tamaño m × n .
Entonces, (A + B) también es una array de m × n
Además, A t y B t son arrays de n × m .
Entonces, la transposición de (A + B) o (A + B) t es una array de n × m .
Ahora podemos decir que A t + B t también es una array de n × m .
Ahora, de la regla de transposición,
(j, i)-ésimo elemento de (A + B) t = (i, j)-ésimo elemento de (A + B)
= (i, j) elemento de A + (i, j) elemento de B
= (j, i) elemento de A t + (j, i) elemento de B t
= (j, i) elemento de B de (A t + B t )
Por lo tanto,
(A + B) t = UN t + B t
Ejemplo:
Dejar,

y
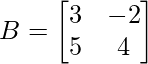
Demostrar que para estas arrays, (A + B) t = A t + B t
Solución:
Encuentra LHS,
Asi que,
Buscar RHS
y,
Ahora,
Por lo tanto,
(A + B) t = UN t + B t
Publicación traducida automáticamente
Artículo escrito por SoumikMondal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA