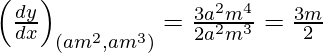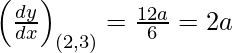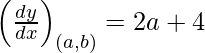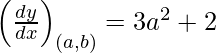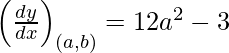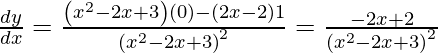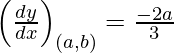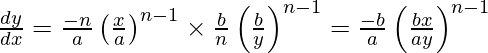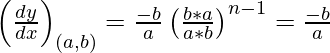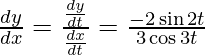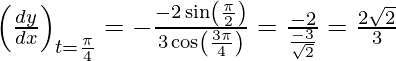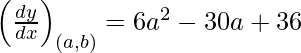Clase 12 Soluciones RD Sharma – Capítulo 16 Tangentes y normales – Ejercicio 16.2

Pregunta 7. Encuentra la ecuación de la normal a la curva ay ² = x ³ en el punto (am ² , am ³ ).

Solución:

Tenemos,

ay ² = x ³

Al diferenciar ambos lados de x, obtenemos

2aydy/dx = 3x ²

dy/dx = 3x ² /2ay

Pendiente de la tangente = $\left(\frac{dy}{dx} \right)_{\left( a m^2 , a m^3 \right)} =\frac{3 a^2 m^4}{2 a^2 m^3}=\frac{3m}{2}$

Dado (x ₁ , y ₁ ) = (am ² , am ³ )

La ecuación de la normal es,

y – y ₁ = -1/m (x – x ₁ )

y – am ³ = -2m/3 (x – am ² )

3my – 3am ⁴ = – 2x + 2am ²

2x + 3my – am ² (2 + 3m ² ) = 0

Pregunta 8. La ecuación de la tangente en (2, 3) sobre la curva y ² = ax ³ + b es y = 4x − 5. Encuentra los valores de a y b.

Solución:

Tenemos,

y ² = hacha ³ + b

Al diferenciar ambos lados de x, obtenemos

2y dy/dx = 3ax ²

dy/dx = 3ax ² /2y

Pendiente de la tangente, m = $\left( \frac{dy}{dx} \right)_{\left( 2, 3 \right)} =\frac{12a}{6}=2a$

La ecuación de la tangente viene dada por y – y ₁ = m (tangente) (x – x ₁ )

Ahora compare la pendiente de una tangente con la ecuación dada

2a = 4

un = 2

Ahora (2, 3) se encuentra en la curva, estos puntos deben satisfacer

32 = 2 (23) + segundo

b = – 7

Pregunta 9. Encuentra la ecuación de la recta tangente a la curva y = x ² + 4x − 16 que es paralela a la recta 3x − y + 1 = 0.

Solución:

Tenemos,

y = x2 ⁺ 4x − 16

Sean (a, b) el punto de intersección de la curva y la tangente.

Como (a, b) se encuentra en la curva, obtenemos

b = un ² + 4a − 16

Ahora, x ² + 4x − 16

dy/dx = 2x + 4

Pendiente de la tangente = $\left( \frac{dy}{dx} \right)_{\left( a , b \right)}=2 a +4$

Dado que la tangente es paralela a la recta que tenemos,

Pendiente de la tangente = Pendiente de la recta dada

=> 2a + 4 = 3

=> 2 a = -1

=> a = -1/2

De la ecuación (1), obtenemos

b = 1/4 – 2 – 16 = -71/4

Ahora, pendiente de la tangente, m = 3

(a, b) = (-1/2, -71/4)

La ecuación de la tangente es,

y – y ₁ = metro (x – x ₁ )

y + 71/4 = 3 (x + 1/2)

$\frac{4y + 71}{4} = 3\left( \frac{2x + 1}{2} \right)$

4y + 71 = 12x + 6

12x – 4y – 65 = 0

Pregunta 10. Encuentra una ecuación de recta normal a la curva y = x ³ + 2x + 6 que sea paralela a la recta x+ 14y + 4 = 0.

Solución:

Tenemos,

y = x ³ + 2x + 6

Sean (a, b) un punto en la curva donde necesitamos encontrar la normal.

Pendiente de la recta dada = -1/14

Como el punto está sobre la curva, obtenemos

b = un ³ + 2a + 6

Ahora, y = x ³ + 2x + 6

dy/dx = 3 x ² + 2

Pendiente de la tangente, m = $\left( \frac{dy}{dx} \right)_{\left( a , b \right)} =3 {a}^2 +2$

Pendiente de la normal = $\frac{- 1}{3 {a}^2 + 2}$

Dado que, pendiente de la normal = pendiente de la recta dada, tenemos

$\frac{- 1}{3 {a}^2 + 2} = \frac{- 1}{14}$

3a ² + 2 = 14

3a ² = 12

un ² = 4

a = ±2

Entonces, b = 18 o -6.

Y pendiente de la normal = -1/14

Cuando a = 2 y b = 18, tenemos

y – y ₁ = metro (x – x ₁ )

y-18 = -1/14 (x-2)

14y – 252 = -x + 2

x + 14y – 254 = 0

Cuando a = -2 y b = -6, tenemos

y – y ₁ = metro (x – x ₁ )

y + 6 = -1/14 (x + 2)

14y + 84 = -x – 2

x + 14y + 86 = 0

Pregunta 11. Determina la(s) ecuación(es) de la recta tangente(s) a la curva y = 4x ³ − 3x + 5 que son perpendiculares a la recta 9y + x + 3 = 0.

Solución:

Sean (a, b) un punto en la curva donde necesitamos encontrar la(s) tangente(s).

Pendiente de la recta dada = -1/9

Como la tangente es perpendicular a la recta dada,

Pendiente de la tangente = $\frac{- 1}{\left( \frac{- 1}{9} \right)}$ = 9

Por lo tanto, b = 4 a ³ – 3 a + 5

Ahora, y = 4 x ³ – 3x + 5

dy/dx = 12 x ² – 3

Pendiente de la tangente = $\left( \frac{dy}{dx} \right)_{\left( a , b \right)} =12 {a}^2 - 3$

Dado que, pendiente de la tangente = pendiente de la recta perpendicular

12a ² – 3 = 9

12a ² = 12

un ² = 1

a = ±1

Entonces, b = 6 o 4.

Por lo tanto, pendiente de la tangente = 9.

Cuando a = 1 y b = 6, tenemos

y – y ₁ = metro (x – x ₁ )

y-6 = 9 (x-1)

y-6 = 9x-9

9x-y-3 = 0

Cuando a = -1 y b = 4, tenemos

y – y ₁ = metro (x – x ₁ )

y – 4 = 9 (x + 1)

y-4 = 9x + 9

9x – y + 13 = 0

Pregunta 12. Encuentra la ecuación de una normal a la curva y = x log _e x que es paralela a la línea 2x − 2y + 3 = 0.

Solución:

La pendiente de la recta dada es 1.

Sean (a, b) el punto donde se traza la tangente a la curva.

Por lo tanto, b = a log _e a . . . . (1)

Ahora, y = x log _e x

dy/dx = x × 1/x + log _e x(1) = 1 + log _e x ₁

Pendiente de la tangente = 1 + log a

Pendiente de la normalidad = $\frac{- 1}{1 + \log_e a}$

Dado que, pendiente de normal = pendiente de la línea dada.

$\frac{- 1}{1 + \log_e a} = 1$

=> -1 = 1 + log a

=> – 2 = iniciar sesión

=> a = e- ²

De (1), tenemos

Ahora, b = e ^-2 (-2) = -2 e ^-2

Dado, (x ₁ , y ₁ ) = (e ^-2 , -2 e ^-2 )

La ecuación de la normal es,

y + 2/e ² = 1(x – 1/e ² )

y + 2/e ² = x – 1/e ²

x – y = 3/e ²

Pregunta 13. Encuentra la ecuación de la recta tangente a la curva y = x ² − 2x + 7

(i) ¿cuál es paralela a la línea 2x − y + 9 = 0?

Solución:

Tenemos, y = x ² − 2x + 7

Al diferenciar ambos lados, obtenemos

dy/dx = 2x – 2

La ecuación de la recta es 2x – y + 9 = 0

Entonces la pendiente de la recta es 2.

Según la pregunta,

=> 2x – 2 = 2

=> 2x = 4

=> x = 2

=> y = 2 ² − 2(2) + 7 = 4 – 4 + 7 = 7

Como (x ₁ , y ₁ ) es (2, 7), la ecuación de la tangente es,

y-7 = 2(x-2)

y-7 = 2x-4

y-2x-3 = 0

(ii) que es perpendicular a la línea 5y − 15x = 13.

Solución:

Tenemos, y = x ² − 2x + 7

Al diferenciar ambos lados, obtenemos

dy/dx = 2x – 2

La ecuación de la recta es 5y − 15x = 13.

=> y = 3x + 13/5

Entonces la pendiente de la recta es 3.

Según la pregunta,

=> 2x – 2= -1/3

=> 6x – 6 = -1

=> x = 5/6

Y y = 217/36.

Como (x ₁ , y ₁ ) es (5/6, 217/36), la ecuación de la tangente es,

y – y ₁ = metro (x – x ₁ )

y – 217/36 = (-1/3) (x – 5/6)

36y -217 = -12x + 10

36y + 12x – 227 = 0

Pregunta 14. Encuentra las ecuaciones de todas las rectas que tienen pendiente 2 y que son tangentes a la curva y = 1/x – 3, x ≠ 3.

Solución:

Sea (a, b) el punto donde se traza la tangente a esta curva.

Dado que el punto se encuentra en la curva, por lo tanto, b = 1/(a – 3)

$\frac{dy}{dx} = \frac{- 1}{\left( x - 3 \right)^2}$

Pendiente de la tangente, m = $\left( \frac{dy}{dx} \right)=\frac{- 1}{\left( a - 3 \right)^2}$

Pendiente de la tangente} = 2

$\frac{- 1}{\left( a - 3 \right)^2} = 2$

(a – 3) ² = – 2

a – 3 = √-2, que no existe porque 2 es negativo.

Entonces, no existe tal tangente.

Pregunta 15. Encuentra las ecuaciones de todas las rectas de pendiente cero y que son tangentes a la curva 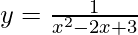$y = \frac{1}{x^2 - 2x + 3}$ .

Solución:

La pendiente de la tangente dada es 0.

Sean (a, b) un punto donde se dibuja la tangente a la curva.

Dado que el punto se encuentra en la curva, entonces b = $\frac{1}{{a}^2 - 2 a + 3}$ . . . . (1)

$\frac{dy}{dx} = \frac{\left( x^2 - 2x + 3 \right)\left( 0 \right) - \left( 2x - 2 \right)1}{\left( x^2 - 2x + 3 \right)^2} = \frac{- 2x + 2}{\left( x^2 - 2x + 3 \right)^2}$

Pendiente de la tangente = $\frac{- 2 a + 2}{\left( {a}^2 - 2 a + 3 \right)^2}$

Dado que, pendiente de la tangente = pendiente de la recta dada,

$\frac{- 2 a + 2}{\left( {a}^2 - 2 a + 3 \right)^2} = 0$

=> -2 a + 2 = 0

=> 2a = 2

=> un = 1

De (1), obtenemos

Ahora, b = $\frac{1}{1 - 2 + 3} = \frac{1}{2}$

(a, b) = (1, 1/2)

La ecuación de la tangente es,

y – y ₁ = metro (x – x ₁ )

y-1/2 = 0 (x-1)

y = 1/2

Pregunta 16. Encuentra la ecuación de la tangente a la curva 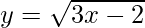$y = \sqrt{3x - 2}$ que es paralela a la 4x − 2y + 5 = 0.

Solución:

Tenemos,

$y = \sqrt{3x - 2}$

Sea (a, b) el punto donde se traza la tangente a la curva y = $\sqrt{3x - 2}$

Al diferenciar ambos lados, obtenemos

$\frac{dy}{dx} = \frac{3}{2\sqrt{3x - 2}}$

Pendiente de la tangente en (a, b) = $\frac{3}{2\sqrt{3 a - 2}}$

La pendiente de la recta 4x − 2y + 5 = 0 es 2.

Dado que, pendiente de la tangente = pendiente de la recta dada

$\frac{3}{2\sqrt{3 a - 2}} = 2$

$3 = 4\sqrt{3 a - 2}$

9 = 16 (3a – 2)

9/16 = 3a – 2

3a = 9/16 + 2

a = 41/48

Ahora, b = $\sqrt{\frac{123}{48} - 2} = \sqrt{\frac{27}{48}} = \sqrt{\frac{9}{16}} = \frac{3}{4}$

Por lo tanto, (a, b) = (41/48, 3/4)

La ecuación de la tangente es,

y – y ₁ = metro (x – x ₁ )

y-3/4 = 2 (x-41/48)

(4y – 3)/4 = 2 (48x – 41)/48

24y – 18 = 48x – 41

48x – 24y – 23 = 0

Pregunta 17. Encuentra la ecuación de la tangente a la curva x ² + 3y − 3 = 0, que es paralela a la recta y= 4x − 5.

Solución:

Suponga que (a, b) es el punto requerido.

Podemos encontrar la pendiente de la recta dada derivando la ecuación wrt x,

Entonces, pendiente de la línea = 4

Como (a, b) se encuentra en la curva, obtenemos a ² + 3b − 3 = 0 . . . . (1)

Ahora,

2x + 3dy/dx = 0

dy/dx = -2x/3

Pendiente de la tangente, m= $\left( \frac{dy}{dx} \right)_{\left( a , b \right)} =\frac{- 2a}{3}$

Dado que la tangente es paralela a la recta, entonces obtenemos,

Pendiente de la tangente, m = pendiente de la recta dada

=> -2a/3 = 4

=> un = -6

De (1), obtenemos

=> 36 + 3b – 3 = 0

=> 3b = – 33

=> segundo = – 11

(a, b) = (-6, -11)

La ecuación de la tangente es,

y – y ₁ = metro (x – x ₁ )

y + 11 = 4 (x + 6)

y + 11 = 4x + 24

4x – y + 13 = 0

Pregunta 18. Demostrar que 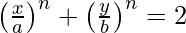$\left( \frac{x}{a} \right)^n + \left( \frac{y}{b} \right)^n = 2$ toca a la recta 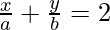$\frac{x}{a} + \frac{y}{b} = 2$ para todo n ∈ N, en el punto (a, b) ?

Solución:

Tenemos,

$\left( \frac{x}{a} \right)^n + \left( \frac{y}{b} \right)^n = 2$

Al diferenciar ambos lados, obtenemos

$\frac{n}{a} \left( \frac{x}{a} \right)^{n - 1} + \frac{n}{b} \left( \frac{y}{b} \right)^{n - 1} \frac{dy}{dx} = 0$

$\frac{n}{b} \left( \frac{y}{b} \right)^{n - 1} \frac{dy}{dx} = \frac{- n}{a} \left( \frac{x}{a} \right)^{n - 1}$

$\frac{dy}{dx} = \frac{- n}{a} \left( \frac{x}{a} \right)^{n - 1} \times \frac{b}{n} \left( \frac{b}{y} \right)^{n - 1} = \frac{- b}{a} \left( \frac{bx}{ay} \right)^{n - 1}$

Pendiente de la tangente = $\left( \frac{dy}{dx} \right)_{\left( a, b \right)} =\frac{- b}{a} \left( \frac{b * a}{a * b} \right)^{n - 1} =\frac{- b}{a}$

La ecuación de la tangente es,

y – b = -b/a (x – a)

ya – ab = – xb + ab

xb + ya = 2ab

$\frac{x}{a} + \frac{y}{b} = 2$

Entonces, la línea dada toca la curva dada en el punto dado.

Por lo tanto probado.

Pregunta 19. Encuentra la ecuación de la tangente a la curva x = sen 3t, y = cos 2t en t = π/4.

Solución:

Tenemos,

x = sen 3t, y = cos 2t

dx/dt = 3 cos3t y dy/dt = -2sen2t

$\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{- 2 \sin 2t}{3 \cos 3t}$

Pendiente de la tangente, m= $\left( \frac{dy}{dx} \right)_{t = \frac{\pi}{4}} =-\frac{- 2 \sin \left( \frac{\pi}{2} \right)}{3 \cos \left( \frac{3\pi}{4} \right)}=\frac{- 2}{\frac{- 3}{\sqrt{2}}}=\frac{2\sqrt{2}}{3}$

x ₁ = sen 3π/4 = 1/√2 y y ₁ = cos π/2 = 0

Entonces, (x ₁ , y ₁ ) = (1/√2, 0)

La ecuación de la tangente es,

y – y ₁ = metro (x – x ₁ )

$y - 0 = \frac{2\sqrt{2}}{3}\left( x - \frac{1}{\sqrt{2}} \right)$

3y = 2√2x – 2

2√2x – 3y – 2 = 0

Pregunta 20. ¿En qué puntos las tangentes a la curva y = 2x ³ − 15x ² + 36x − 21 serán paralelas al eje x? Además, encuentre las ecuaciones de las tangentes a la curva en estos puntos.

Solución:

Tenemos,

y = 2x ³ − 15x ² + 36x − 21

La pendiente del eje x es 0.

Sea (a, b) el punto requerido.

Como (a, b) está sobre la curva, obtenemos

segundo = 2a ³ – 15a ² + 36a – 21 . . . . (1)

Además, tenemos

dy/dx = 6 x ² – 30x + 36

Pendiente de la tangente en (a, b) = $\left( \frac{dy}{dx} \right)_{\left( a , b \right)} = 6 {a}^2 - 30 a + 36$

Dado que la pendiente de la tangente = pendiente del eje x, tenemos

=> 6a ² – 30a + 36 = 0

=> un ² – 5a + 6 = 0

=> (un – 2) (un – 3) = 0

=> a = 2 o a = 3

=> b = 7 o 6

Cuando a = 2 y b = 7, la ecuación es,

y – y ₁ = metro (x – x ₁ )

y-7 = 0 (x-2)

y = 7

Cuando a = 3 y b = 6, la ecuación es,

y – y ₁ = metro (x – x ₁ )

y-6 = 0 (x-3)

y = 6

Pregunta 21. Encuentra la ecuación de las tangentes a la curva 3x ² – y ² = 8, que pasa por el punto (4/3, 0).

Solución:

Tenemos,

3x ² – y ² = 8 . . . . (1)

Al diferenciar ambos lados de x, obtenemos

6x – 2y dy/dx = 0

2y dy/dx = 6x

dy/dx = 6x/2y

dy/dx = 3x/y

Deje que la tangente en (h, k) pase por (4/3, 0). Como (h, k) se encuentra en (1), obtenemos

3 h ² – k ² = 8 . . . (ii)

Pendiente de la tangente en (h, k) = 3h/k

La ecuación de la tangente en (h, k) viene dada por,

y-k = 3h/k (x-h)

También,

=> 0 – k = (3h/k) (4/3 – h)

=> -k = 4h/k – 3h2 ^/ k

=> – k2 ⁼ 4h – ^3h2

=> 8 – 3 h ² = 4 h – 3 h ²

=> 8 = 4 horas

=> h = 2

También obtenemos,

=> 12 – k2 = ⁸

=> k ² = 4

=> k = ±2

Entonces, los puntos en la curva (i) en los que las tangentes pasan por (4/3, 0) son (2, ±2).

Cuando h = 2 y k = 2, la ecuación es,

y-2 = (6/2) (x-2)

3x-y-4 = 0

Cuando h = 2 y k = –2, la ecuación es,

y + 2 = (6/-2) (x – 2)

3x + y – 4 = 0

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 16 Tangentes y normales – Ejercicio 16.2 | conjunto 2

Pregunta 7. Encuentra la ecuación de la normal a la curva ay ² = x ³ en el punto (am ² , am ³ ).

Pregunta 8. La ecuación de la tangente en (2, 3) sobre la curva y ² = ax ³ + b es y = 4x − 5. Encuentra los valores de a y b.

Pregunta 9. Encuentra la ecuación de la recta tangente a la curva y = x ² + 4x − 16 que es paralela a la recta 3x − y + 1 = 0.

Pregunta 10. Encuentra una ecuación de recta normal a la curva y = x ³ + 2x + 6 que sea paralela a la recta x+ 14y + 4 = 0.

Pregunta 11. Determina la(s) ecuación(es) de la recta tangente(s) a la curva y = 4x ³ − 3x + 5 que son perpendiculares a la recta 9y + x + 3 = 0.

Pregunta 12. Encuentra la ecuación de una normal a la curva y = x log _e x que es paralela a la línea 2x − 2y + 3 = 0.

Pregunta 13. Encuentra la ecuación de la recta tangente a la curva y = x ² − 2x + 7

(i) ¿cuál es paralela a la línea 2x − y + 9 = 0?

(ii) que es perpendicular a la línea 5y − 15x = 13.

Pregunta 14. Encuentra las ecuaciones de todas las rectas que tienen pendiente 2 y que son tangentes a la curva y = 1/x – 3, x ≠ 3.

Pregunta 15. Encuentra las ecuaciones de todas las rectas de pendiente cero y que son tangentes a la curva $y = \frac{1}{x^2 - 2x + 3}$ .

Pregunta 16. Encuentra la ecuación de la tangente a la curva $y = \sqrt{3x - 2}$ que es paralela a la 4x − 2y + 5 = 0.

Pregunta 17. Encuentra la ecuación de la tangente a la curva x ² + 3y − 3 = 0, que es paralela a la recta y= 4x − 5.

Pregunta 18. Demostrar que $\left( \frac{x}{a} \right)^n + \left( \frac{y}{b} \right)^n = 2$ toca a la recta $\frac{x}{a} + \frac{y}{b} = 2$ para todo n ∈ N, en el punto (a, b) ?

Pregunta 19. Encuentra la ecuación de la tangente a la curva x = sen 3t, y = cos 2t en t = π/4.

Pregunta 20. ¿En qué puntos las tangentes a la curva y = 2x ³ − 15x ² + 36x − 21 serán paralelas al eje x? Además, encuentre las ecuaciones de las tangentes a la curva en estos puntos.

Pregunta 21. Encuentra la ecuación de las tangentes a la curva 3x ² – y ² = 8, que pasa por el punto (4/3, 0).

Deja una respuesta Cancelar la respuesta

Pregunta 7. Encuentra la ecuación de la normal a la curva ay 2 = x 3 en el punto (am 2 , am 3 ).

Pregunta 8. La ecuación de la tangente en (2, 3) sobre la curva y 2 = ax 3 + b es y = 4x − 5. Encuentra los valores de a y b.

Pregunta 9. Encuentra la ecuación de la recta tangente a la curva y = x 2 + 4x − 16 que es paralela a la recta 3x − y + 1 = 0.

Pregunta 10. Encuentra una ecuación de recta normal a la curva y = x 3 + 2x + 6 que sea paralela a la recta x+ 14y + 4 = 0.

Pregunta 11. Determina la(s) ecuación(es) de la recta tangente(s) a la curva y = 4x 3 − 3x + 5 que son perpendiculares a la recta 9y + x + 3 = 0.

Pregunta 12. Encuentra la ecuación de una normal a la curva y = x log e x que es paralela a la línea 2x − 2y + 3 = 0.

Pregunta 13. Encuentra la ecuación de la recta tangente a la curva y = x 2 − 2x + 7

(i) ¿cuál es paralela a la línea 2x − y + 9 = 0?

(ii) que es perpendicular a la línea 5y − 15x = 13.

Pregunta 14. Encuentra las ecuaciones de todas las rectas que tienen pendiente 2 y que son tangentes a la curva y = 1/x – 3, x ≠ 3.

Pregunta 15. Encuentra las ecuaciones de todas las rectas de pendiente cero y que son tangentes a la curva .

Pregunta 16. Encuentra la ecuación de la tangente a la curva que es paralela a la 4x − 2y + 5 = 0.

Pregunta 17. Encuentra la ecuación de la tangente a la curva x 2 + 3y − 3 = 0, que es paralela a la recta y= 4x − 5.

Pregunta 18. Demostrar que toca a la recta para todo n ∈ N, en el punto (a, b) ?

Pregunta 19. Encuentra la ecuación de la tangente a la curva x = sen 3t, y = cos 2t en t = π/4.

Pregunta 20. ¿En qué puntos las tangentes a la curva y = 2x 3 − 15x 2 + 36x − 21 serán paralelas al eje x? Además, encuentre las ecuaciones de las tangentes a la curva en estos puntos.

Pregunta 21. Encuentra la ecuación de las tangentes a la curva 3x 2 – y 2 = 8, que pasa por el punto (4/3, 0).

Deja una respuesta Cancelar la respuesta

Pregunta 7. Encuentra la ecuación de la normal a la curva ay ² = x ³ en el punto (am ² , am ³ ).

Pregunta 8. La ecuación de la tangente en (2, 3) sobre la curva y ² = ax ³ + b es y = 4x − 5. Encuentra los valores de a y b.

Pregunta 9. Encuentra la ecuación de la recta tangente a la curva y = x ² + 4x − 16 que es paralela a la recta 3x − y + 1 = 0.

Pregunta 10. Encuentra una ecuación de recta normal a la curva y = x ³ + 2x + 6 que sea paralela a la recta x+ 14y + 4 = 0.

Pregunta 11. Determina la(s) ecuación(es) de la recta tangente(s) a la curva y = 4x ³ − 3x + 5 que son perpendiculares a la recta 9y + x + 3 = 0.

Pregunta 12. Encuentra la ecuación de una normal a la curva y = x log _e x que es paralela a la línea 2x − 2y + 3 = 0.

Pregunta 13. Encuentra la ecuación de la recta tangente a la curva y = x ² − 2x + 7

Pregunta 15. Encuentra las ecuaciones de todas las rectas de pendiente cero y que son tangentes a la curva $y = \frac{1}{x^2 - 2x + 3}$ .

Pregunta 16. Encuentra la ecuación de la tangente a la curva $y = \sqrt{3x - 2}$ que es paralela a la 4x − 2y + 5 = 0.

Pregunta 17. Encuentra la ecuación de la tangente a la curva x ² + 3y − 3 = 0, que es paralela a la recta y= 4x − 5.

Pregunta 18. Demostrar que $\left( \frac{x}{a} \right)^n + \left( \frac{y}{b} \right)^n = 2$ toca a la recta $\frac{x}{a} + \frac{y}{b} = 2$ para todo n ∈ N, en el punto (a, b) ?

Pregunta 20. ¿En qué puntos las tangentes a la curva y = 2x ³ − 15x ² + 36x − 21 serán paralelas al eje x? Además, encuentre las ecuaciones de las tangentes a la curva en estos puntos.

Pregunta 21. Encuentra la ecuación de las tangentes a la curva 3x ² – y ² = 8, que pasa por el punto (4/3, 0).