Cualquier expresión algebraica con constantes y variables se conoce como polinomio. Polinomio es una combinación de dos palabras, «Poli» y «nominal», donde poli significa «muchos» y nominal significa «términos», por lo tanto, un polinomio puede contener tantos términos pero nunca infinitos. En un polinomio, los ceros y los coeficientes están presentes donde los coeficientes ya se nos proporcionan; sin embargo, necesitamos obtener el valor de los ceros con la ayuda de los coeficientes.
Relación entre ceros y coeficientes
Sabemos que los ceros de cualquier polinomio son los puntos donde la gráfica del polinomio corta el eje x. Estos ceros también se pueden encontrar usando los coeficientes de diferentes términos en un polinomio. Veamos la relación entre los ceros y los coeficientes de los polinomios.
polinomio lineal
Un polinomio lineal, en general, se define por,
y = hacha + b
Lo sabemos, para los ceros necesitamos encontrar los puntos en los que y = 0. Resolviendo esta ecuación general para y = 0.
y = hacha + b
⇒0 = hacha + b
⇒x = ![]()
Esto nos da la relación entre cero y el coeficiente de un polinomio lineal.
En general, para una ecuación lineal y = ax + b, a ≠ 0, la gráfica de ax + b es una línea recta que corta el eje x en ( ,
0)
Pregunta: Verifique los ceros del polinomio lineal tanto usando la fórmula mencionada anteriormente como el método gráfico.
y = 4x + 2
Solución:
Nos dan con la ecuación y = 4x + 2,
Aquí a = 4 y b = 2
Entonces, por la fórmula mencionada anteriormente, el cero ocurrirá en (
, 0) que es
Verifiquemos este cero con el método gráfico. Necesitamos trazar la gráfica de esta ecuación.
y = 4x + 2
Llevémoslo a la forma de intercepción.
Ahora conocemos las intersecciones en los ejes x e y.
Polinomio cuadrático
Los polinomios cuadráticos tienen el grado más alto de 2 y, junto con la factorización, existen otros métodos a través de los cuales se pueden encontrar los ceros del polinomio cuadrático, como el método Dharacharya . Como tiene el grado más alto 2, existen 2 ceros en un polinomio cuadrático.
Derivamos la relación entre ceros y coeficientes de un polinomio cuadrático. Supongamos un polinomio,
P(x) = 2x 2 – 8x + 6
Este polinomio se puede factorizar de la siguiente manera,
P(x) = 2x 2 -8x + 6
= 2x 2 – 6x – 2x + 6
= 2x(x-3) -2(x-3)
= 2(x-1)(x-3)
Entonces esta ecuación tiene raíces x = 1 y x = 3
Darse cuenta de,
Suma de ceros = 1 + 3 = 4 =
Producto de ceros = 1 × 3 = 3 =
Esta es la relación entre ceros y coeficientes para coeficientes de segundo orden.
Así que para poner en una forma general
Para un polinomio, p(x) = ax 2 + bx + c que tiene m y n como raíces
metro + norte =
metro × norte =
Pregunta: Verifica la propiedad indicada arriba para la ecuación, 6x 2 – 10x + 4
Solución:
6x 2 – 10x + 4
⇒ 6x 2 – 6x -4x + 4
⇒ 6x(x – 1) – 4(x – 1)
⇒ (6x – 4) (x – 1)
Por lo tanto, las raíces de esta ecuación resultan ser x =
y x = 1
Ahora sabemos de acuerdo con las propiedades anteriores,
Suma de ceros =
Producto de ceros =
vamos a verificarlo
Sol de ceros = 1 +
=
Ambos valores llegan a ser iguales. Por lo tanto, verificado.
Verifiquemos la propiedad del producto de raíces
Producto de ceros =
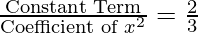
En este caso también, ambos valores son iguales. Por lo tanto, verificado.
Polinomio cúbico
Se puede derivar una relación similar para un polinomio cúbico. Un polinomio cúbico es un polinomio de grado 3 y como su mayor grado es 3, existen tres ceros de un polinomio cúbico. Supongamos que las raíces/ceros de los polinomios obtenidos son p, q, r, la relación entre los ceros y los polinomios vendrá dada por,
Para un polinomio cúbico,
hacha 3 + bx 2 + cx + d
Que tiene raíces x = p, q y r
pag + q+ r =
pq + qr + pr =
pqr =
Veamos algunos ejemplos con respecto a estas propiedades.
Problemas de muestra
Pregunta 1: Verifica que -1,1,2 son las raíces del polinomio x 3 -2x 2 – x + 2. Además , verifica las propiedades indicadas anteriormente.
Solución:
x = -1, 1 y 2 son las raíces del polinomio que es P(x) = 0 en todos estos puntos. Introduzcamos los valores de x uno por uno en el polinomio.
P(-1) = (-1) 3 – 2(-1) 2 -(-1) + 2
= -1 – 2 + 1 + 2
= -3 + 3
= 0
P(1) = (1) 3 – 2(1) 2 – 1 + 2
= 1 – 2 – 1 + 2
= 0
P(2) = (2) 3 – 2(2) 2 – 2 + 2
= 8 – 8 – 2 + 2
= 0
Por lo tanto, todos estos puntos son raíces del polinomio
Verifiquemos las propiedades
(1) p + q+ r =
⇒ -1 + 1+ 2 =
⇒ 2 = 2
LHS = RHS
Por lo tanto verificado
(2) pq + qr + pr =
⇒ (-1)(1) + (1)(2) + (-1)(2) =
⇒ -1+ 2 -2 = -1
⇒ -1 = -1
LHS = RHS
Por lo tanto verificado
(3) pqr =
⇒ (-1)(1)(2) =
⇒ -2 = -2
LHS = RHS
Por lo tanto verificado
Pregunta 2: Evalúa la suma y el producto de los ceros del polinomio cuadrático 6x 2 + 18.
Solución:
La forma general de un polinomio cuadrático es ax 2 + bx + c = 0.
Dado el polinomio 6x 2 + 18 se puede reescribir como,
6x 2 + 0.x + 18
Como se estudió anteriormente, la suma y el producto de las raíces del polinomio cuadrático viene dada por,
metro + norte =
mn =
Donde m y n son las raíces del polinomio
En nuestro caso a = 6, b = 0 y c = 18. Introduciendo los valores en las fórmulas
metro + norte =
mn =
Por lo tanto, la suma de raíces es 0 y el producto está dado por 3.
Pregunta 3: Dado un polinomio ax 2 + bx + 1. Sus raíces son -1 y 3. Encuentra los valores de a y b.
Solución:
Conocemos la fórmula de la suma y el producto de la raíz de un polinomio cuadrático.
Sean m y n las raíces,
Aquí, m = -1 y n =3
Entonces, por la fórmula
metro + norte =
…(1)
min =
…..(2)
De la ecuación (1)
-1 + 3 =
⇒ 2 = \frac{-b}{a}
⇒ 2a = -b
De la ecuación (2)
(-1)(3) =
⇒ -3a = 1
⇒ un =

Poniendo este valor de «a» en la ecuación anterior
segundo =
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
