Clase 11 Soluciones RD Sharma – Capítulo 15 Inecuaciones lineales – Ejercicio 15.2 | conjunto 2

Pregunta 11. Resuelve cada uno de los siguientes sistemas de ecuaciones en R: 4x – 1 ≤ 0, 3 – 4x < 0

Solución:

Sea la primera ecuación 4x – 1 ≤ 0

⇒ 4x ≤ 1

⇒ x ≤ 1/4

y la segunda ecuación sea 3 – 4x < 0

⇒ 4x > 3

⇒ x > 3/4

Según la primera ecuación, x se encuentra en el rango (-∞, 1/4] y según la segunda ecuación, x se encuentra en el rango (3/4, -∞)

Calculando la intersección de estos dos intervalos no obtenemos valor para x. Por lo tanto, un conjunto dado de inecuaciones no tiene solución.

Pregunta 12. Resuelve cada uno de los siguientes sistemas de ecuaciones en R: x + 5 > 2(x+1), 2 – x < 3(x+2)

Solución:

Sea la primera ecuación x + 5 > 2(x+1)

⇒ x + 5 > 2x + 2

⇒ x < 3

y la segunda ecuación sea 2 – x < 3(x+2)

⇒ 2 – x < 3x + 6

⇒ -4 < 4x

⇒ x > -1

Por lo tanto, usando las ecuaciones anteriores, sabemos que x se encuentra en el rango (-1,3)

Pregunta 13. Resuelve cada uno de los siguientes sistemas de ecuaciones en R: 2(x – 6) < 3x – 7, 11 – 2x < 6 – x

Solución:

Sea la primera ecuación 2(x – 6) < 3x – 7

⇒ 2x – 12 < 3x – 7

⇒ -x < 5

⇒ x > -5

y la segunda ecuación sea 11 – 2x < 6 – x

⇒ -x < -5

⇒ x > 5

Por lo tanto, usando las ecuaciones anteriores, sabemos que x se encuentra en el rango (5,∞)

Pregunta 14. Resuelve cada uno de los siguientes sistemas de ecuaciones en R: 5x – 7 < 3 (x + 3), 1 – 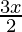  ≥ x – 4

Solución:

Sea la primera ecuación 5x – 7 < 3 (x + 3)

⇒ 5x-7 < 3x + 9

⇒ 2x < 16

⇒ x < 8

y la segunda ecuación be1 –  ≥ x – 4

⇒ x +   ≤ 5

⇒   < 5

⇒ \frac{x}{2} ≤ 1

⇒ x ≤ 2

Por lo tanto, usando las ecuaciones anteriores, sabemos que x se encuentra en el rango [-∞, 2]

Pregunta 15. Resuelve cada uno de los siguientes sistemas de ecuaciones en R: 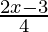  -2 ≥ 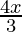  – 6, 2(2x + 3) < 6(x – 2) + 10

Solución:

Sea la primera ecuación   -2 ≥   – 6

⇒   –   ≥ – 6 + 2

⇒   ≥ -4

⇒ 6x – 9 -16x ≥ -48

⇒ 10x ≤ 39

⇒ x ≤ 

y la segunda ecuación sea 2(2x + 3) < 6(x – 2) + 10

⇒ 4x + 6 < 6x -12 + 10

⇒ -2x < -8

⇒ x > 4

Según la primera ecuación, x se encuentra en el rango (-∞, 39/10] y según la segunda ecuación, x se encuentra en el rango (4, ∞)

Calculando la intersección de estos dos intervalos no obtenemos valor para x. Por lo tanto, un conjunto dado de inecuaciones no tiene solución.

Pregunta 16. Resuelve cada uno de los siguientes sistemas de ecuaciones en R: 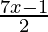  < -3, 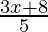  + 11 < 0

Solución:

Sea la primera ecuación   < -3

⇒ 7x – 1 < -6

⇒ 7x < -5

⇒ x < -5/7

y la segunda ecuación sea   + 11 < 0

⇒ 3x + 8 < -55

⇒ 3x < -63

⇒ x < -21

Por lo tanto, usando las ecuaciones anteriores, sabemos que x se encuentra en el rango (-∞, -21)

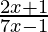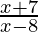Pregunta 17. Resuelve cada uno de los siguientes sistemas de ecuaciones en R:   > 5,  > 2

Solución:

Sea la primera ecuación   > 5

⇒ 2x + 1 > 5 (7x -1)

⇒ 2x – 35x > -6

⇒ – 33x > -6

⇒ x < 2/11

Además, 7x -1 > 0 ⇒ x > 1/7

usando la primera ecuación que obtenemos, x se encuentra en el rango 

y sea la segunda ecuación   > 2

⇒ x + 7 > 2x – 16

⇒ 23 > x

⇒ x < 23

Además, x – 8 > 0 ⇒ x > 8

Por lo tanto, usando las ecuaciones anteriores, sabemos que x se encuentra en el rango (8, -23)

Calculando la intersección de los dos intervalos que obtenemos después de resolver la ecuación 1 y la ecuación 2, no obtenemos ningún valor para x. Por lo tanto, un conjunto dado de inecuaciones no tiene solución.

Pregunta 18. Resuelva cada uno de los siguientes sistemas de ecuaciones en R: 0 < 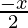  < 3

Solución:

Usando la ecuación, 0 <   < 3

⇒ 0 < -x < 6

⇒ 0 > x > -6

⇒ x > -5

Por lo tanto, usando la ecuación anterior, sabemos que x se encuentra en el rango (-6, 0)

Pregunta 19. Resuelve cada uno de los siguientes sistemas de ecuaciones en R: 10 ≤ -5 (x – 2) < 20

Solución:

Sea la primera ecuación 10 ≤ -5 (x – 2) < 20

⇒ 10 ≤ -5x + 10 < 20

⇒ 0 ≤ -5x < 10

⇒ 0 ≤ x < -2

Por lo tanto, usando las ecuaciones anteriores, sabemos que x se encuentra en el rango (-2, 0]

Pregunta 20. Resuelve cada uno de los siguientes sistemas de ecuaciones en R: -5 < 2x -3 < 5

Solución:

Usando la ecuación -5 < 2x -3 < 5

⇒ -2 < 2x < 8

⇒ -1 < x < 4

Por lo tanto, usando las ecuaciones anteriores, sabemos que x se encuentra en el rango (-1, 4)

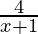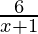Pregunta 21. Resuelve cada uno de los siguientes sistemas de ecuaciones en R:   ≤ 3 ≤  , x>0

Solución:

Usando la ecuación   ≤ 3 ≤  , x>0

⇒ 4 ≤ 3 (x+1) ≤ 6

⇒ 4 ≤ 3x + 3 ≤ 6

⇒ 4 ≤ 3x + 3 ≤ 6

⇒ 1 ≤ 3x ≤ 3

⇒ 1/3 ≤ x ≤ 1

Por lo tanto, usando las ecuaciones anteriores, sabemos que x se encuentra en el rango