Camino más corto en un gráfico de complemento

Dado un gráfico no ponderado no dirigido G . Para un inicio de Node dado, devuelva el camino más corto que es el número de aristas desde el inicio hasta todos los Nodes en el gráfico complementario de G.

Complement Graph es un gráfico tal que contiene solo aquellos bordes que no están presentes en el gráfico original.

Ejemplos:

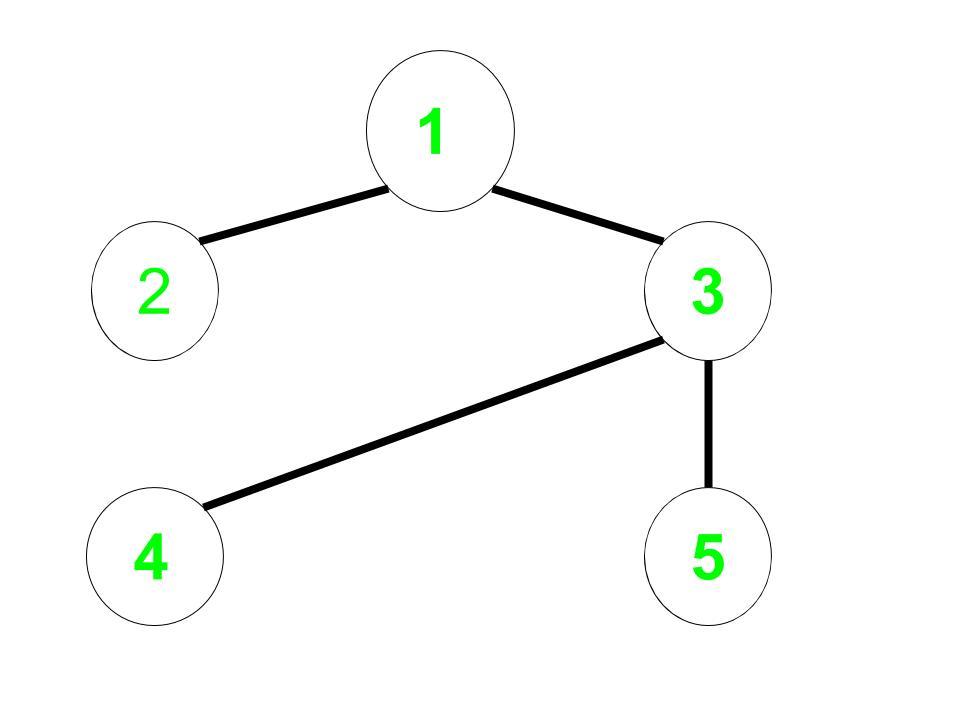
Entrada: Aristas no dirigidas = (1, 2), (1, 3), (3, 4), (3, 5), Inicio = 1 
Salida: 0 2 3 1 1 
Explicación: 
Gráfico original:

Gráfico de complemento: 
 

La distancia de 1 a cada Node en el gráfico del complemento es: 
1 a 1 = 0, 
1 a 2 = 2, 
1 a 3 = 3, 
1 a 4 = 1, 
1 a 5 = 1

Enfoque ingenuo: una solución simple será crear el gráfico complementario y usar la búsqueda primero en amplitud en este gráfico para encontrar la distancia a todos los Nodes.
Complejidad temporal: O(n ² ) para crear el gráfico de complemento y O(n + m) para la búsqueda en amplitud.
Enfoque eficiente: la idea es utilizar la búsqueda primero en amplitud modificada para calcular la respuesta y luego no hay necesidad de construir el gráfico de complemento.

• Para cada vértice o Node, reduzca la distancia de un vértice que es un complemento del vértice actual y aún no ha sido descubierto.
• Para el problema, debemos observar que si el gráfico es disperso, los Nodes no descubiertos se visitarán muy rápido.

A continuación se muestra la implementación del enfoque anterior:

// C++ implementation to find the
// shortest path in a complement graph
 
#include <bits/stdc++.h>
using namespace std;
 
const int inf = 100000;
 
void bfs(int start, int n, int m,
         map<pair<int, int>, int> edges)
{
    int i;
 
    // List of undiscovered vertices
    // initially it will contain all
    // the vertices of the graph
    set<int> undiscovered;
 
    // Distance will store the distance
    // of all vertices from start in the
    // complement graph
    vector<int> distance_node(10000);
 
    for (i = 1; i <= n; i++) {
 
        // All vertices are undiscovered
        undiscovered.insert(i);
 
        // Let initial distance be infinity
        distance_node[i] = inf;
    }
 
    undiscovered.erase(start);
    distance_node[start] = 0;
    queue<int> q;
 
    q.push(start);
 
    // Check if queue is not empty and the
    // size of undiscovered vertices
    // is greater than 0
    while (undiscovered.size() && !q.empty()) {
        int cur = q.front();
        q.pop();
 
        // Vector to store all the complement
        // vertex to the current vertex
        // which has not been
        // discovered or visited yet.
        vector<int> complement_vertex;
 
        for (int x : undiscovered) {
           
            if (edges.count({ cur, x }) == 0 &&
                edges.count({ x, cur })==0)
                complement_vertex.push_back(x);
        }
        for (int x : complement_vertex) {
 
            // Check if optimal change
            // the distance of this
            // complement vertex
            if (distance_node[x]
                > distance_node[cur] + 1) {
                distance_node[x]
                    = distance_node[cur] + 1;
                q.push(x);
            }
 
            // Finally this vertex has been
            // discovered so erase it from
            // undiscovered vertices list
            undiscovered.erase(x);
        }
    }
    // Print the result
    for (int i = 1; i <= n; i++)
        cout << distance_node[i] << " ";
}
 
// Driver code
int main()
{
    // n is the number of vertex
    // m is the number of edges
    // start - starting vertex is 1
    int n = 5, m = 4;
 
    // Using edge hashing makes the
    // algorithm faster and we can
    // avoid the use of adjacency
    // list representation
    map<pair<int, int>, int> edges;
 
    // Initial edges for
    // the original graph
    edges[{ 1, 3 }] = 1,
                 edges[{ 3, 1 }] = 1;
    edges[{ 1, 2 }] = 1,
                 edges[{ 2, 1 }] = 1;
    edges[{ 3, 4 }] = 1,
                 edges[{ 4, 3 }] = 1;
    edges[{ 3, 5 }] = 1,
                 edges[{ 5, 3 }] = 1;
 
    bfs(1, n, m, edges);
 
    return 0;
}

// Java implementation to find the
// shortest path in a complement graph
import java.io.*;
import java.util.*;
 
class GFG{
     
// Pair class is made so as to
// store the edges between nodes
static class Pair
{
    int left;
    int right;
     
    public Pair(int left, int right)
    {
        this.left = left;
        this.right = right;
    }
     
    // We need to override hashCode so that
    // we can use Set's properties like contains()
    @Override
    public int hashCode()
    {
        final int prime = 31;
        int result = 1;
        result = prime * result + left;
        result = prime * result + right;
        return result;
    }
 
    @Override
    public boolean equals( Object other )
    {
        if (this == other){return true;}
        if (other instanceof Pair)
        {
            Pair m = (Pair)other;
            return this.left == m.left &&
                  this.right == m.right;
        }
        return false;
    }
}
 
public static void bfs(int start, int n, int m,
                       Set<Pair> edges)
{
    int i;
 
    // List of undiscovered vertices
    // initially it will contain all
    // the vertices of the graph
    Set<Integer> undiscovered = new HashSet<>();
 
    // Distance will store the distance
    // of all vertices from start in the
    // complement graph
    int[] distance_node = new int[1000];
 
    for(i = 1; i <= n; i++)
    {
 
        // All vertices are undiscovered initially
        undiscovered.add(i);
 
        // Let initial distance be maximum value
        distance_node[i] = Integer.MAX_VALUE;
    }
     
    // Start is discovered
    undiscovered.remove(start);
     
    // Distance of the node to itself is 0
    distance_node[start] = 0;
     
    // Queue used for BFS
    Queue<Integer> q = new LinkedList<>();
 
    q.add(start);
 
    // Check if queue is not empty and the
    // size of undiscovered vertices
    // is greater than 0
    while (undiscovered.size() > 0 && !q.isEmpty())
    {
         
        // Current node
        int cur = q.peek();
        q.remove();
 
        // Vector to store all the complement
        // vertex to the current vertex
        // which has not been
        // discovered or visited yet.
        List<Integer>complement_vertex = new ArrayList<>();
 
        for(int x : undiscovered)
        {
            Pair temp1 = new Pair(cur, x);
            Pair temp2 = new Pair(x, cur);
             
            // Add the edge if not already present
            if (!edges.contains(temp1) &&
                !edges.contains(temp2))
            {
                complement_vertex.add(x);
            }
        }
         
        for(int x : complement_vertex)
        {
             
            // Check if optimal change
            // the distance of this
            // complement vertex
            if (distance_node[x] >
                distance_node[cur] + 1)
            {
                distance_node[x] =
                distance_node[cur] + 1;
                q.add(x);
            }
 
            // Finally this vertex has been
            // discovered so erase it from
            // undiscovered vertices list
            undiscovered.remove(x);
        }
    }
     
    // Print the result
    for(i = 1; i <= n; i++)
        System.out.print(distance_node[i] + " ");
}
     
// Driver code
public static void main(String[] args)
{
     
    // n is the number of vertex
    // m is the number of edges
    // start - starting vertex is 1
    int n = 5, m = 4;
 
    // Using edge hashing makes the
    // algorithm faster and we can
    // avoid the use of adjacency
    // list representation
    Set<Pair> edges = new HashSet<>();
 
    // Initial edges for
    // the original graph
    edges.add(new Pair(1, 3));
    edges.add(new Pair(3, 1));
    edges.add(new Pair(1, 2));
    edges.add(new Pair(2, 1));
    edges.add(new Pair(3, 4));
    edges.add(new Pair(4, 3));
    edges.add(new Pair(3, 5)) ;
    edges.add(new Pair(5, 3));
    Pair t = new Pair(1, 3);
 
    bfs(1, n, m, edges);
}
}
 
// This code is contributed by kunalsg18elec

0 2 3 1 1

Complejidad temporal: O(V+E) 
Espacio auxiliar: O(V)