Clase 12 RD Sharma Solutions – Capítulo 29 El avión – Ejercicio 29.3

Pregunta 1. Encuentra la ecuación vectorial de un plano que pasa por un punto que tiene posición vectorial 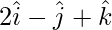$2\sombrero{i}-\sombrero{j}+\sombrero{k}$ y es perpendicular al vector $4\sombrero{i}+2\sombrero{j}-3\sombrero{k}$ .

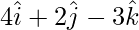Solución:

Como sabemos que la ecuación vectorial de un plano que pasa por un punto $\vec{a}$ y es normal a $\vec{n}$ es

$(\vec{r}-\vec{a}).\vec{n} =0$

⇒ $\vec{r}.\vec{n}=\vec{a}.\vec{n}$

aquí, $\vec{a}=2\hat{i}-\hat{j}+\hat{k}$ y $\vec{n}=4\sombrero{i}+2\sombrero{j}-3\sombrero{k}$

Entonces, la ecuación de la ecuación requerida es

$\vec{r}.(4\sombrero{i}+2\sombrero{j}-3\sombrero{k})=(2\sombrero{i}-\sombrero{j}+\sombrero{k})( 4\sombrero{i}+2\sombrero{j}-3\sombrero{k})$

⇒ $\vec{r}.(4\sombrero{i}+2\sombrero{j}-3\sombrero{k})$ = (4)(2) + (2)(-1) + (-3)(1)

⇒ $\vec{r}.(4\sombrero{i}+2\sombrero{j}-3\sombrero{k})$ = 8 – 2 – 3

⇒ $\vec{r}.(4\sombrero{i}+2\sombrero{j}-3\sombrero{k})=3$

Por lo tanto, la ecuación requerida es

$\vec{r}.(4\hat{i}+2\hat{j}-3\hat{k})-3=0$

Pregunta 2. Encuentra la forma cartesiana de la ecuación de un plano cuya ecuación vectorial es

(i) 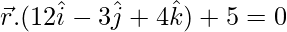$\vec{r}.(12\hat{i}-3\hat{j}+4\hat{k})+5=0$

Solución:

Dada la ecuación vectorial de un plano,

$\vec{r}.(12\hat{i}-3\hat{j}+4\hat{k})+5=0$

Dado que $\hat{i}, \hat{j}, \hat{k}$ denota el vector de posición de un punto arbitrario (x, y, z) en el plano.

Por lo tanto, poner $\vec{r}=x\hat{i}+y\hat{j}+j\hat{k}$

⇒ $(x\hat{i}+y\hat{j}+j\hat{k}).(12\hat{i}-3\hat{j}+4\hat{k})+5=0$

⇒

⇒ 12x – 3y + 4z + 5 = 0

Entonces, esta es la ecuación cartesiana requerida del plano.

(ii) 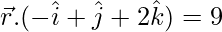$\vec{r}.(-\hat{i}+\hat{j}+2\hat{k})=9$

Solución:

Dada la ecuación vectorial de un plano,

$\vec{r}.(-\hat{i}+\hat{j}+2\hat{k})=9$

Dado que $\hat{i}, \hat{j}, \hat{k}$ denota el vector de posición de un punto arbitrario (x, y, z) en el plano.

Por lo tanto, poner $\vec{r}=x\hat{i}+y\hat{j}+j\hat{k}$

⇒ $(x\hat{i}+y\hat{j}+j\hat{k}).(-\hat{i}+\hat{j}+2\hat{k})=9$

⇒

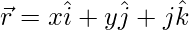
⇒ -x + y + 2z = 9

Entonces, esta es la ecuación cartesiana requerida del plano.

Pregunta 3. Encuentra la ecuación vectorial de los planos de coordenadas.

Solución:

Ecuación vectorial del plano XY:

El Plano XY pasa por el origen cuyo vector de posición es $\vec{a}=\vec{0}$ y

perpendicular al eje Z cuyo vector de posición es $\vec{k}$

Entonces la ecuación del plano XY es $\vec{r}.\vec{n}=\vec{a}.\vec{n}$

⇒ $\vec{r}.\vec{k}=\vec{0}.\vec{k}$

$\vec{r}.\vec{k}=0$

Ecuación vectorial de XZ-Plane:

El plano XZ pasa por el origen cuyo vector de posición es $\vec{a}=\vec{0}$

y perpendicular al eje Y cuyo vector de posición es $\vec{j}$

Entonces la ecuación del plano XZ es $\vec{r}.\vec{n}=\vec{a}.\vec{n}$

⇒ $\vec{r}.\vec{j}=\vec{0}.\vec{j}$

$\vec{r}.\vec{j} =0$

Ecuación vectorial del plano YZ:

El Plano YZ- pasa por el origen cuyo vector de posición es $\vec{a}=\vec{0}$

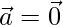
y perpendicular al eje X cuyo vector de posición es $\vec{i}$

Entonces la ecuación del plano YZ es $\vec{r}.\vec{n}=\vec{a}.\vec{n}$

⇒ $\vec{r}.\vec{i}=\vec{0}.\vec{i}$

$\vec{r}.\vec{i}=0$

Por lo tanto, la ecuación vectorial de los planos de coordenadas.

Plano XY = $\vec{r}.\vec{k}=0$

Plano XZ = $\vec{r}.\vec{j}=0$

YZ-Plano = $\vec{r}.\vec{i}=0$

Pregunta 4. Encuentra la ecuación vectorial de cada uno de los siguientes planos:

(yo) 2x – y + 2z =8

Solución:

Dada la ecuación del plano es,

2x – y + 2z = 8

Asi que,

$(x\hat{i}+y\hat{j}+z\hat{k})(2\hat{i}-\hat{j}+2\hat{k})=8$

$\vec{r}.(2\hat{i}-\hat{j}+2\hat{k})=8$

Por lo tanto, la ecuación vectorial del plano es $\vec{r}.(2\hat{i}-\hat{j}+2\hat{k})=8$

(ii) x + y – z =5

Solución:

Dada la ecuación del plano es,

x + y – z = 5

Asi que,

$(x\hat{i}+y\hat{j}+z\hat{k})(\hat{i}+\hat{j}-\hat{k})=5$

$\vec{r}.(\hat{i}+\hat{j}-\hat{k})=5$

Por lo tanto, la ecuación vectorial del plano es $\vec{r}.(\hat{i}+\hat{j}-\hat{k})=5$

(iii) x + y = 3

Solución:

Dada la ecuación del plano es,

x + y = 3

Asi que,

$(x\hat{i}+y\hat{j}+z\hat{k})(\hat{i}+\hat{j})=3$

$\vec{r}.(\hat{i}+\hat{j})=3$

Por lo tanto, la ecuación vectorial del plano es $\vec{r}.(\hat{i}+\hat{j})=3$

Pregunta 5. Hallar las ecuaciones vectoriales y cartesianas de un plano que pasa por el punto (1, -1, 1) y es normal a la recta que une los puntos (1, 2, 5) y (-1, 3, 1).

Solución:

Como sabemos que la ecuación vectorial de un plano que pasa por un punto $\vec{a}$ y es normal a $\vec{n}$ es

$(\vec{r}-\vec{a}).\vec{n} = 0$ …..(1)

Entonces, según la pregunta se da que el plano pasa por el punto (1, -1, 1) y

normal a la recta que une los puntos A(1, 2, 5) y B(-1, 3, 1).

Asi que,

$\vec{a}=\hat{i}-\hat{j}+\hat{k}$

$\vec{n}=\overrightarrow{AB}$

$\overrightarrow{AB}$ = Vector de posición de $\vec{B}$ – Vector de posición de $\vec{A}$

= $(-\hat{i}+3\hat{j}+\hat{k})-(\hat{i}+2\hat{j}+5\hat{k})$

= $-2\hat{i}+\hat{j}-4\hat{k}$

Ahora, de la ecuación (1), obtenemos

$[\vec{r}-(\hat{i}-\hat{j}+\hat{k})].(-2\hat{i}+\hat{j}-4\hat{k})=0$

⇒ $\vec{r}.(-2\hat{i}+\hat{j}-4\hat{k})-(\hat{i}-\hat{j}+\hat{k}).(-2\hat{i}+\hat{j}-4\hat{k})=0$

⇒ $\vec{r}.(-2\hat{i}+\hat{j}-4\hat{k})-[-2-1-4]=0$

⇒ $\vec{r}.(-2\hat{i}+\hat{j}-4\hat{k})+7=0$

⇒ $\vec{r}.(-2\hat{i}+\hat{j}-4\hat{k})=-7$

⇒ $\vec{r}.(2\hat{i}-\hat{j}+4\hat{k})=7$ …(2)

Ahora, $\vec{r}=x\hat{i}+y\hat{j}+j\hat{k}$ introduciendo la ecuación (2), obtenemos

$(x\hat{i}+y\hat{j}+j\hat{k}).(2\hat{i}-\hat{j}+4\hat{k})=7$

2x – y + 4z = 7

Entonces, la ecuación vectorial es el plano es $\vec{r}.(2\hat{i}-\hat{j}+4\hat{k})=7$

y la ecuación cartesiana del plano es 2x – y + 4z = 7

Pregunta 6. Si 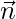$\vec{n}$ es un vector de magnitud √3 y está igualmente inclinado con un ángulo agudo con los ejes coordenados. Encuentre las formas vectorial y cartesiana de la ecuación de un plano que pasa por (2, 1, -1) y es normal a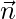 $\vec{n}$

Solución:

Dado que $\vec{n}$ = √3 y $\vec{n}$ forma ángulo igual con los ejes coordenados.

Consideremos que $\vec{n}$ tiene coseno director como u, v y w, y

forma ángulo de α, β y γ con los ejes de coordenadas.

Entonces, α = β = γ

cos α = cos β = cos γ

Suponiendo que u = v = w = p

Lo sabemos

tu ² + v ² + w ² = 1

pag ² + pag ² + pag ² = 1

P2 ⁼ 1/3

P= ±1/√3

Asi que,

tu = ±1/√3

cos α = ±1/√3

Ahora, α = cos ^-1 (-1/√3)

Da, α es un ángulo obtuso, así que ignórelo.

Ahora, α = cos ^-1 (1/√3)

Da, α es un ángulo agudo, entonces

cos α = ±1/√3

tu = v = w = 1/√3

Asi que,

$\vec{n} = |\vec{n}|(l\vec{i}+m\vec{j}+n\vec{k})$

= √3 $(\frac{1}{√3}\vec{i}+\frac{1}{√3}\vec{j}+\frac{1}{√3}\vec{k})$

Ahora, $\vec{n}=\hat{i}+\hat{j}+\hat{k}$ y $\vec{a}=2\hat{i}+\hat{j}-\hat{k}$

Como sabemos que la ecuación vectorial de un plano que pasa por un punto $\vec{a}$ y es normal a $\vec{n}$ es

$(\vec{r}-\vec{a}).\vec{n}=0$

$[\vec{r}-(2\hat{i}+\hat{j}-\hat{k})].(\hat{i}+\hat{j}+\hat{k})=0$

⇒ $\vec{r}(\hat{i}+\hat{j}+\hat{k})-(2\hat{i}+\hat{j}-\hat{k})(\hat{i}+\hat{j}+\hat{k})=0$

⇒ $\vec{r}(\hat{i}+\hat{j}+\hat{k})-(2+1-1)=0$

⇒ $\vec{r}(\hat{i}+\hat{j}+\hat{k})=2$ ….(1)

Ahora, $\vec{r}=x\hat{i}+y\hat{j}+j\hat{k}$ introduciendo la ecuación (1), obtenemos

⇒ $(x\hat{i}+y\hat{j}+j\hat{k})(\hat{i}+\hat{j}+\hat{k})=2$

⇒ x + y + z = 2

Por lo tanto, la ecuación vectorial del plano es $\vec{r}(\hat{i}+\hat{j}+\hat{k})=2$

y la ecuación cartesiana del plano es x + y + z = 2

Pregunta 7. Las coordenadas del pie de la perpendicular trazada desde el origen a un plano son (12, -4, 3). Encuentra la ecuación del plano.

Solución:

De acuerdo a la pregunta se da que las coordenadas del pie de la

la perpendicular trazada desde el origen O a un plano es P(12, -4, 3)

Así, podemos decir que el plano buscado pasa por P(12, -4, 3) y es perpendicular a OP.

Como sabemos que la ecuación vectorial de un plano que pasa por un punto $\vec{a}$ y es normal a $\vec{n}$ es

$(\vec{r}-\vec{a}).\vec{n}=0$ …….(1)

Aquí, $\vec{a}=12\sombrero{i}-4\sombrero{j}+3\sombrero{k}$

$\vec{n}=(12\sombrero{i}-4\sombrero{j}+3\sombrero{k})-(0\sombrero{i}+0\sombrero{j}+0\sombrero{k} )$

$\vec{n}=12\sombrero{i}-4\sombrero{j}+3\sombrero{k}$

Al poner los valores de $\vec{a}$ y $\vec{n}$ en la ecuación (1)

$[\vec{r}-(12\hat{i}-4\hat{j}+3\hat{k})].(12\hat{i}-4\hat{j}+3\hat{ k})=0$

⇒ $\vec{r}(12\sombrero{i}-4\sombrero{j}+3\sombrero{k})-(12\sombrero{i}-4\sombrero{j}+3\sombrero{k}) (12\sombrero{i}-4\sombrero{j}+3\sombrero{k})=0$

⇒ $\vec{r}(12\sombrero{i}-4\sombrero{j}+3\sombrero{k})-[(12)(12)+(-4)(-4)+(3)(3 )]=0$

⇒ $\vec{r}(12\sombrero{i}-4\sombrero{j}+3\sombrero{k})-(144+16+9)=0$

⇒ $\vec{r}(12\sombrero{i}-4\sombrero{j}+3\sombrero{k})=169$ ……..(2)

Ahora, al poner $\vec{r}=x\sombrero{i}+y\sombrero{j}+z\sombrero{k}$ en la ecuación (2), obtenemos

⇒ $(x\sombrero{i}+y\sombrero{j}+z\sombrero{k})(12\sombrero{i}-4\sombrero{j}+3\sombrero{k})-169=0$

⇒ 12x – 4y + 3z = 169

Por lo tanto, la ecuación vectorial del plano es $\vec{r}(12\sombrero{i}-4\sombrero{j}+3\sombrero{k})=169$

y la ecuación cartesiana del plano es 12x- 4y+ 3z = 169

Pregunta 8. Encuentra la ecuación del plano que pasa por el punto (2, 3, 1) dado que las relaciones de dirección de la normal al plano son proporcionales a (5, 3, 2).

Solución:

Según la pregunta se da que el avión pasa por P(2, 3, 1)

teniendo (5, 3, 2) como las relaciones de dirección de la normal al plano.

Como sabemos que la ecuación vectorial de un plano que pasa por un punto $\vec{a}$ y es normal a $\vec{n}$ es

$(\vec{r}-\vec{a}).\vec{n}=0$ …..(i)

Asi que, $\vec{a}=2\sombrero{i}+3\sombrero{j}+\sombrero{k}$

$\vec{n}=5\sombrero{i}+3\sombrero{j}+2\sombrero{k}$

Ahora ponga todos estos valores en la ecuación (i),

$[\vec{r}-(2\hat{i}+3\hat{j}+\hat{k})].(5\hat{i}+3\hat{j}+2\hat{k})=0$

$\vec{r}(5\hat{i}+3\hat{j}+2\hat{k})-(2\hat{i}+3\hat{j}+\hat{k})(5\hat{i}+3\hat{j}+2\hat{k})=0$

$\vec{r}(5\hat{i}+3\hat{j}+2\hat{k})-[(2)(5)+(3)(3)+(1)(2)]=0$

$\vec{r}(5\hat{i}+3\hat{j}+2\hat{k})-[10+9+2]=0$

$\vec{r}(5\hat{i}+3\hat{j}+2\hat{k})-21=0$ ………(2)

Ahora, poniendo, $\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$ en la ecuación (2), obtenemos

$(x\hat{i}+y\hat{j}+z\hat{k})(5\hat{i}+3\hat{j}+2\hat{k})-21=0$

(x)(5) + (y)(3) + (z)(2) = 21

5x + 3y + 2z = 21

Por lo tanto, esta es la ecuación requerida del plano

Pregunta 9. Si los ejes son perpendiculares y P es el punto (2, 3, -1), encuentre la ecuación del plano que pasa por P en ángulo recto con OP.

Solución:

Según la pregunta se da que P es el punto (2,3,-1) y

el plano pasa por P y OP es el vector normal al plano.

Asi que,

Como sabemos que la ecuación vectorial de un plano que pasa por un punto $\vec{a}$ y es normal a $\vec{n}$ es

$(\vec{r}-\vec{a}).\vec{n}=0$ …..(i)

Aquí, $\vec{a}=2\hat{i}+3\hat{j}-\hat{k}$

$\vec{n}=\overrightarrow{OP}$

Entonces, $\overrightarrow{OP}$ = Vector de posición de P – Vector de posición de O

= $(2\hat{i}+3\hat{j}-\hat{k})-(0\hat{i}+0\hat{j}+0\hat{k})$

$\vec{n}=(2\hat{i}+3\hat{j}-\hat{k})$

Ahora ponga, el valor de $\vec{a}$ y $\vec{n}$ en la ecuación (i),

$[\vec{r}-(2\hat{i}+3\hat{j}-\hat{k})].(2\hat{i}+3\hat{j}-\hat{k})=0$

$\vec{r}(2\hat{i}+3\hat{j}-\hat{k})-[2\hat{i}+3\hat{j}-\hat{k})(2\hat{i}+3\hat{j}-\hat{k})]=0$

$\vec{r}(2\hat{i}+3\hat{j}-\hat{k})-[(2)(2)+(3)(3)+(-1)(-1)]=0$

$\vec{r}(2\hat{i}+3\hat{j}-\hat{k})-[4+9+1]=0$

$\vec{r}(2\hat{i}+3\hat{j}-\hat{k})=14$ ……..(2)

Ahora poniendo, $\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$ , en la ecuación (2), obtenemos

$(x\hat{i}+y\hat{j}+z\hat{k})(2\hat{i}+3\hat{j}-\hat{k})=14$

Entonces, esta es la ecuación requerida del plano.

Pregunta 10. Encuentra las intersecciones hechas en los ejes de coordenadas por el plano 2x + y -2z = 3 y encuentra también los cosenos directores de la normal al plano.

Solución:

Según la pregunta

La ecuación del plano os = 2x + y -2z = 3

Ahora dividimos ambos lados de la ecuación por 3, obtenemos

$\frac{2x}{3}+\frac{y}{3}-\frac{2z}{3}=\frac{3}{3}$

$\frac{x}{3/2}{}+\frac{y}{3}+\frac{z}{-3/2}=1$ ……(i)

Aquí, si a, b, c son las intersecciones de un plano en los ejes de coordenadas,

entonces la ecuación del plano es:

$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$ ……(ii)

Al comparar la ecuación (i) y (ii), obtenemos el valor de a, b y c

$a=\frac{3}{2}, b=\frac{3}{1}, c=-\frac{3}{2}$

Entonces, de la ecuación del plano dada,

$(x\hat{i}+y\hat{j}+z\hat{k})(2\hat{i}+\hat{j}-2\hat{k})=3$

$\vec{r}(2\hat{i}+\hat{j}-2\hat{k})=3$

Por lo tanto, el vector normal al plano es,

$\vec{n}=2\hat{i}+\hat{j}-2\hat{k}$

$|\vec{n}|$ = √{(2) ² + (1) ² + (-2) ² }

= √(4 + 1 + 4)

= √9

$|\vec{n}|=3$

Por lo tanto, el vector unitario perpendicular a $\vec{n}= \frac{\vec{n}}{|\vec{n}|}= \frac{2\vec{i} + \vec{j}-2\vec{k}}{3}$

Por tanto, el coseno director de la normal al plano = 2/3, 1/3, -2/3

Publicación traducida automáticamente

Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 RD Sharma Solutions – Capítulo 29 El avión – Ejercicio 29.3 | Serie 1

Pregunta 1. Encuentra la ecuación vectorial de un plano que pasa por un punto que tiene posición vectorial $2\sombrero{i}-\sombrero{j}+\sombrero{k}$ y es perpendicular al vector $4\sombrero{i}+2\sombrero{j}-3\sombrero{k}$ .

Pregunta 2. Encuentra la forma cartesiana de la ecuación de un plano cuya ecuación vectorial es

(i) $\vec{r}.(12\hat{i}-3\hat{j}+4\hat{k})+5=0$

(ii) $\vec{r}.(-\hat{i}+\hat{j}+2\hat{k})=9$

Pregunta 3. Encuentra la ecuación vectorial de los planos de coordenadas.

Pregunta 4. Encuentra la ecuación vectorial de cada uno de los siguientes planos:

(yo) 2x – y + 2z =8

(ii) x + y – z =5

(iii) x + y = 3

Pregunta 5. Hallar las ecuaciones vectoriales y cartesianas de un plano que pasa por el punto (1, -1, 1) y es normal a la recta que une los puntos (1, 2, 5) y (-1, 3, 1).

Pregunta 6. Si $\vec{n}$ es un vector de magnitud √3 y está igualmente inclinado con un ángulo agudo con los ejes coordenados. Encuentre las formas vectorial y cartesiana de la ecuación de un plano que pasa por (2, 1, -1) y es normal a $\vec{n}$

Pregunta 7. Las coordenadas del pie de la perpendicular trazada desde el origen a un plano son (12, -4, 3). Encuentra la ecuación del plano.

Pregunta 8. Encuentra la ecuación del plano que pasa por el punto (2, 3, 1) dado que las relaciones de dirección de la normal al plano son proporcionales a (5, 3, 2).

Pregunta 9. Si los ejes son perpendiculares y P es el punto (2, 3, -1), encuentre la ecuación del plano que pasa por P en ángulo recto con OP.

Pregunta 10. Encuentra las intersecciones hechas en los ejes de coordenadas por el plano 2x + y -2z = 3 y encuentra también los cosenos directores de la normal al plano.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra la ecuación vectorial de un plano que pasa por un punto que tiene posición vectorial y es perpendicular al vector .

Pregunta 2. Encuentra la forma cartesiana de la ecuación de un plano cuya ecuación vectorial es

(i)

(ii)

Pregunta 3. Encuentra la ecuación vectorial de los planos de coordenadas.

Pregunta 4. Encuentra la ecuación vectorial de cada uno de los siguientes planos:

(yo) 2x – y + 2z =8

(ii) x + y – z =5

(iii) x + y = 3

Pregunta 5. Hallar las ecuaciones vectoriales y cartesianas de un plano que pasa por el punto (1, -1, 1) y es normal a la recta que une los puntos (1, 2, 5) y (-1, 3, 1).

Pregunta 6. Si es un vector de magnitud √3 y está igualmente inclinado con un ángulo agudo con los ejes coordenados. Encuentre las formas vectorial y cartesiana de la ecuación de un plano que pasa por (2, 1, -1) y es normal a

Pregunta 7. Las coordenadas del pie de la perpendicular trazada desde el origen a un plano son (12, -4, 3). Encuentra la ecuación del plano.

Pregunta 8. Encuentra la ecuación del plano que pasa por el punto (2, 3, 1) dado que las relaciones de dirección de la normal al plano son proporcionales a (5, 3, 2).

Pregunta 9. Si los ejes son perpendiculares y P es el punto (2, 3, -1), encuentre la ecuación del plano que pasa por P en ángulo recto con OP.

Pregunta 10. Encuentra las intersecciones hechas en los ejes de coordenadas por el plano 2x + y -2z = 3 y encuentra también los cosenos directores de la normal al plano.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra la ecuación vectorial de un plano que pasa por un punto que tiene posición vectorial $2\sombrero{i}-\sombrero{j}+\sombrero{k}$ y es perpendicular al vector $4\sombrero{i}+2\sombrero{j}-3\sombrero{k}$ .

(i) $\vec{r}.(12\hat{i}-3\hat{j}+4\hat{k})+5=0$

(ii) $\vec{r}.(-\hat{i}+\hat{j}+2\hat{k})=9$

Pregunta 6. Si $\vec{n}$ es un vector de magnitud √3 y está igualmente inclinado con un ángulo agudo con los ejes coordenados. Encuentre las formas vectorial y cartesiana de la ecuación de un plano que pasa por (2, 1, -1) y es normal a $\vec{n}$