MCD de dos números es el número más grande que los divide a ambos. Una forma sencilla de encontrar el MCD es factorizar ambos números y multiplicar los factores primos comunes.
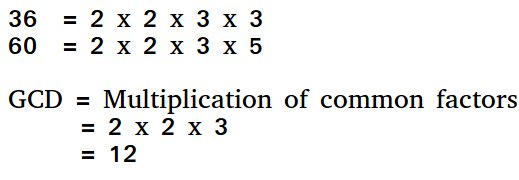
Algoritmo euclidiano básico para GCD: el algoritmo se basa en los siguientes hechos.
- Si restamos un número más pequeño de uno más grande (reducimos un número más grande), GCD no cambia. Entonces, si seguimos restando repetidamente el mayor de dos, terminamos con GCD.
- Ahora, en lugar de restar, si dividimos el número más pequeño, el algoritmo se detiene cuando encontramos el resto 0.
A continuación se muestra una función recursiva para evaluar mcd usando el algoritmo de Euclides.
CPP
// C++ program to demonstrate
// Basic Euclidean Algorithm
#include <bits/stdc++.h>
using namespace std;
// Function to return
// gcd of a and b
int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// Driver Code
int main()
{
int a = 10, b = 15;
cout << "GCD(" << a << ", "
<< b << ") = " << gcd(a, b)
<< endl;
a = 35, b = 10;
cout << "GCD(" << a << ", "
<< b << ") = " << gcd(a, b)
<< endl;
a = 31, b = 2;
cout << "GCD(" << a << ", "
<< b << ") = " << gcd(a, b)
<< endl;
return 0;
}
C
// C program to demonstrate Basic Euclidean Algorithm
#include <stdio.h>
// Function to return gcd of a and b
int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b%a, a);
}
// Driver program to test above function
int main()
{
int a = 10, b = 15;
printf("GCD(%d, %d) = %dn", a, b, gcd(a, b));
a = 35, b = 10;
printf("GCD(%d, %d) = %dn", a, b, gcd(a, b));
a = 31, b = 2;
printf("GCD(%d, %d) = %dn", a, b, gcd(a, b));
return 0;
}
Java
// Java program to demonstrate working of extended
// Euclidean Algorithm
import java.util.*;
import java.lang.*;
class GFG
{
// extended Euclidean Algorithm
public static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b%a, a);
}
// Driver Program
public static void main(String[] args)
{
int a = 10, b = 15, g;
g = gcd(a, b);
System.out.println("GCD(" + a + " , " + b+ ") = " + g);
a = 35; b = 10;
g = gcd(a, b);
System.out.println("GCD(" + a + " , " + b+ ") = " + g);
a = 31; b = 2;
g = gcd(a, b);
System.out.println("GCD(" + a + " , " + b+ ") = " + g);
}
}
// Code Contributed by Mohit Gupta_OMG <(0_o)>
Python3
# Python program to demonstrate Basic Euclidean Algorithm
# Function to return gcd of a and b
def gcd(a, b):
if a == 0 :
return b
return gcd(b%a, a)
a = 10
b = 15
print("gcd(", a , "," , b, ") = ", gcd(a, b))
a = 35
b = 10
print("gcd(", a , "," , b, ") = ", gcd(a, b))
a = 31
b = 2
print("gcd(", a , "," , b, ") = ", gcd(a, b))
# Code Contributed By Mohit Gupta_OMG <(0_o)>
C#
using System;
class GFG
{
public static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// Driver Code
static public void Main ()
{
int a = 10, b = 15, g;
g = gcd(a, b);
Console.WriteLine("GCD(" + a +
" , " + b + ") = " + g);
a = 35; b = 10;
g = gcd(a, b);
Console.WriteLine("GCD(" + a +
" , " + b + ") = " + g);
a = 31; b = 2;
g = gcd(a, b);
Console.WriteLine("GCD(" + a +
" , " + b + ") = " + g);
}
}
// This code is contributed by ajit
PHP
<?php
// PHP program to demonstrate
// Basic Euclidean Algorithm
// Function to return
// gcd of a and b
function gcd($a, $b)
{
if ($a == 0)
return $b;
return gcd($b % $a, $a);
}
// Driver Code
$a = 10; $b = 15;
echo "GCD(",$a,"," , $b,") = ",
gcd($a, $b);
echo "\n";
$a = 35; $b = 10;
echo "GCD(",$a ,",",$b,") = ",
gcd($a, $b);
echo "\n";
$a = 31; $b = 2;
echo "GCD(",$a ,",", $b,") = ",
gcd($a, $b);
// This code is contributed by m_kit
?>
Javascript
<script>
// JavaScript program to demonstrate
// Basic Euclidean Algorithm
// Function to return
// gcd of a and b
function gcd( a, b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// Driver Code
let a = 10, b = 15;
document.write( "GCD(" + a + ", "
+ b + ") = " + gcd(a, b) +"<br/>");
a = 35, b = 10;
document.write( "GCD(" + a + ", "
+ b + ") = " + gcd(a, b) +"<br/>");
a = 31, b = 2;
document.write( "GCD(" + a + ", "
+ b + ") = " + gcd(a, b) +"<br/>");
// This code contributed by aashish1995
</script>
Producción :
GCD(10, 15) = 5 GCD(35, 10) = 5 GCD(31, 2) = 1
Complejidad de tiempo: O(Log min(a, b)), Espacio auxiliar: O(log(min(a,b)).
Algoritmo Euclidiano Extendido:
El algoritmo euclidiano extendido también encuentra coeficientes enteros x e y tales que:
ax + by = gcd(a, b)
Ejemplos:
Input: a = 30, b = 20
Output: gcd = 10
x = 1, y = -1
(Note that 30*1 + 20*(-1) = 10)
Input: a = 35, b = 15
Output: gcd = 5
x = 1, y = -2
(Note that 35*1 + 15*(-2) = 5)
El algoritmo euclidiano extendido actualiza los resultados de gcd(a, b) usando los resultados calculados por la llamada recursiva gcd(b%a, a). Deje que los valores de x e y calculados por la llamada recursiva sean x 1 e y 1 . x e y se actualizan usando las siguientes expresiones.
x = y1 - ⌊b/a⌋ * x1 y = x1
A continuación se muestra una implementación basada en las fórmulas anteriores.
C++
// C++ program to demonstrate working of
// extended Euclidean Algorithm
#include <bits/stdc++.h>
using namespace std;
// Function for extended Euclidean Algorithm
int gcdExtended(int a, int b, int *x, int *y)
{
// Base Case
if (a == 0)
{
*x = 0;
*y = 1;
return b;
}
int x1, y1; // To store results of recursive call
int gcd = gcdExtended(b%a, a, &x1, &y1);
// Update x and y using results of
// recursive call
*x = y1 - (b/a) * x1;
*y = x1;
return gcd;
}
// Driver Code
int main()
{
int x, y, a = 35, b = 15;
int g = gcdExtended(a, b, &x, &y);
cout << "GCD(" << a << ", " << b
<< ") = " << g << endl;
return 0;
}
C
// C program to demonstrate working of extended
// Euclidean Algorithm
#include <stdio.h>
// C function for extended Euclidean Algorithm
int gcdExtended(int a, int b, int *x, int *y)
{
// Base Case
if (a == 0)
{
*x = 0;
*y = 1;
return b;
}
int x1, y1; // To store results of recursive call
int gcd = gcdExtended(b%a, a, &x1, &y1);
// Update x and y using results of recursive
// call
*x = y1 - (b/a) * x1;
*y = x1;
return gcd;
}
// Driver Program
int main()
{
int x, y;
int a = 35, b = 15;
int g = gcdExtended(a, b, &x, &y);
printf("gcd(%d, %d) = %d", a, b, g);
return 0;
}
Java
// Java program to demonstrate working of extended
// Euclidean Algorithm
import java.lang.*;
import java.util.*;
class GFG {
// extended Euclidean Algorithm
public static int gcdExtended(int a, int b, int x,
int y)
{
// Base Case
if (a == 0) {
x = 0;
y = 1;
return b;
}
int x1 = 1,
y1 = 1; // To store results of recursive call
int gcd = gcdExtended(b % a, a, x1, y1);
// Update x and y using results of recursive
// call
x = y1 - (b / a) * x1;
y = x1;
return gcd;
}
// Driver Program
public static void main(String[] args)
{
int x = 1, y = 1;
int a = 35, b = 15;
int g = gcdExtended(a, b, x, y);
System.out.print("gcd(" + a + " , " + b
+ ") = " + g);
}
}
Python3
# Python program to demonstrate working of extended
# Euclidean Algorithm
# function for extended Euclidean Algorithm
def gcdExtended(a, b):
# Base Case
if a == 0:
return b, 0, 1
gcd, x1, y1 = gcdExtended(b % a, a)
# Update x and y using results of recursive
# call
x = y1 - (b//a) * x1
y = x1
return gcd, x, y
# Driver code
a, b = 35, 15
g, x, y = gcdExtended(a, b)
print("gcd(", a, ",", b, ") = ", g)
C#
// C# program to demonstrate working
// of extended Euclidean Algorithm
using System;
class GFG
{
// extended Euclidean Algorithm
public static int gcdExtended(int a, int b,
int x, int y)
{
// Base Case
if (a == 0)
{
x = 0;
y = 1;
return b;
}
// To store results of
// recursive call
int x1 = 1, y1 = 1;
int gcd = gcdExtended(b % a, a, x1, y1);
// Update x and y using
// results of recursive call
x = y1 - (b / a) * x1;
y = x1;
return gcd;
}
// Driver Code
static public void Main ()
{
int x = 1, y = 1;
int a = 35, b = 15;
int g = gcdExtended(a, b, x, y);
Console.WriteLine("gcd(" + a + " , " +
b + ") = " + g);
}
}
PHP
<?php
// PHP program to demonstrate
// working of extended
// Euclidean Algorithm
// PHP function for
// extended Euclidean
// Algorithm
function gcdExtended($a, $b,
$x, $y)
{
// Base Case
if ($a == 0)
{
$x = 0;
$y = 1;
return $b;
}
// To store results
// of recursive call
$gcd = gcdExtended($b % $a,
$a, $x, $y);
// Update x and y using
// results of recursive
// call
$x = $y - floor($b / $a) * $x;
$y = $x;
return $gcd;
}
// Driver Code
$x = 0;
$y = 0;
$a = 35; $b = 15;
$g = gcdExtended($a, $b, $x, $y);
echo "gcd(",$a;
echo ", " , $b, ")";
echo " = " , $g;
?>
Javascript
<script>
// Javascript program to demonstrate
// working of extended
// Euclidean Algorithm
// Javascript function for
// extended Euclidean
// Algorithm
function gcdExtended(a, b,
x, y)
{
// Base Case
if (a == 0)
{
x = 0;
y = 1;
return b;
}
// To store results
// of recursive call
let gcd = gcdExtended(b % a,
a, x, y);
// Update x and y using
// results of recursive
// call
x = y - (b / a) * x;
y = x;
return gcd;
}
// Driver Code
let x = 0;
let y = 0;
let a = 35;
let b = 15;
let g = gcdExtended(a, b, x, y);
document.write("gcd(" + a);
document.write(", " + b + ")");
document.write(" = " + g);
</script>
Producción :
gcd(35, 15) = 5
Complejidad de tiempo: O(logn), Espacio auxiliar: O(logn)
¿Cómo funciona el algoritmo extendido?
As seen above, x and y are results for inputs a and b,
a.x + b.y = gcd ----(1)
And x1 and y1 are results for inputs b%a and a
(b%a).x1 + a.y1 = gcd
When we put b%a = (b - (⌊b/a⌋).a) in above,
we get following. Note that ⌊b/a⌋ is floor(b/a)
(b - (⌊b/a⌋).a).x1 + a.y1 = gcd
Above equation can also be written as below
b.x1 + a.(y1 - (⌊b/a⌋).x1) = gcd ---(2)
After comparing coefficients of 'a' and 'b' in (1) and
(2), we get following
x = y1 - ⌊b/a⌋ * x1
y = x1
¿Cómo es útil el algoritmo extendido?
El algoritmo euclidiano extendido es particularmente útil cuando a y b son coprimos (o gcd es 1). Dado que x es el inverso multiplicativo modular de “a módulo b”, y y es el inverso multiplicativo modular de “b módulo a”. En particular, el cálculo del inverso multiplicativo modular es un paso esencial en el método de cifrado de clave pública RSA.
Este artículo es una contribución de Ankur . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA