Introducción a la trama Bootstrap

Antes de entrar en el diagrama Bootstrap, primero comprendamos de qué se trata Bootstrap (o muestreo Bootstrap). 

Bootstrap Sampling: es un método en el que tomamos una muestra de datos repetidamente con reemplazo de un conjunto de datos para estimar un parámetro de población. Se utiliza para determinar varios parámetros de una población. 

Bootstrap plot: Es un método gráfico utilizado para medir la incertidumbre de cualquier característica estadística deseada de una población. Es una alternativa al intervalo de confianza. (también un método matemático utilizado para el cálculo de una estadística). 

Estructura

• eje x: número de submuestra.
• eje y: valor calculado de la estadística deseada para una submuestra determinada.

Necesidad de un diagrama de Bootstrap:

Comúnmente, podemos calcular matemáticamente la incertidumbre de una estadística de una población, utilizando intervalos de confianza. Sin embargo, en muchos casos, la fórmula de incertidumbre que se obtiene es matemáticamente intratable. En tales casos, usamos el gráfico Bootstrap. 

Supongamos que tenemos 5000 personas en un parque y necesitamos encontrar el peso promedio de toda la población. No es factible medir el peso de cada individuo y luego sacar un promedio de eso. Aquí es donde entra en escena el muestreo de arranque. 

Lo que hacemos es tomar grupos de 5 personas al azar de la población y encontrar su media. Hacemos el mismo proceso, digamos 8-10 veces. De esta forma, conseguimos una buena estimación del peso medio de la población de forma más eficiente. 

Intuición:

Consideremos un ejemplo y comprendamos cómo el gráfico Bootstrap facilita la obtención de información crítica de una gran población. Digamos que tenemos una muestra de datos de 3000 números uniformes generados aleatoriamente. Sacamos una submuestra de 30 números y encontramos su media. Hacemos esto de nuevo para otra submuestra aleatoria y así sucesivamente.  

Trazamos un diagrama de arranque de la información adquirida anteriormente y con solo mirarlo, podemos dar fácilmente una buena estimación sobre la media de todos los 3000 números. Hay otra información útil que se puede obtener de un diagrama de arranque, como:

• qué submuestra tuvo la varianza más baja, o
• qué submuestra crea el intervalo de confianza más estrecho, etc.

Implementación: 

import pandas as pd
import numpy as np
 
s = pd.Series(np.random.uniform(size=500))
pd.plotting.bootstrap_plot(s)

Producción

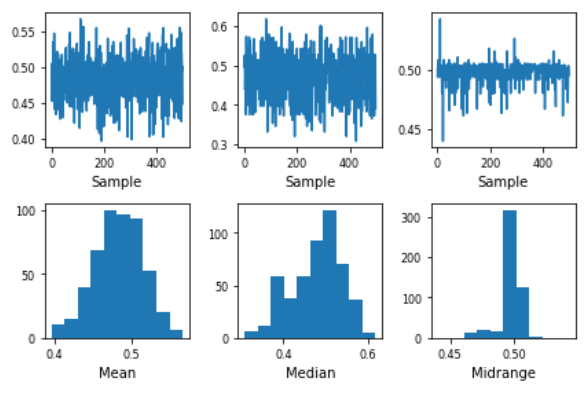
Limitación

1. El diagrama de arranque proporciona una estimación de la información requerida de la población, no los valores exactos.
2. Depende en gran medida del conjunto de datos proporcionado. No da buenos resultados cuando muchos subconjuntos tienen muestras repetidas.
3. El diagrama de arranque se vuelve ineficaz cuando obtenemos información que depende en gran medida de los valores de cola. [Como se muestra en la figura 1]