Cuente los anagramas que tengan el primer carácter como consonante y ningún par de consonantes o vocales colocadas de forma adyacente

Dada una string S de longitud N , la tarea es contar el número de anagramas de S cuyo primer carácter es una consonante y ningún par de consonantes o vocales son adyacentes entre sí.

Ejemplos:

Entrada: S = “GADO”
Salida: 4
Explicación:
Los anagramas de la string S que satisfacen las condiciones dadas son GADO, GODA, DOGA, DAGO.
Por lo tanto, el número total de tales anagramas es 4.

Entrada: S = “AABCY”
Salida: 6
Explicación:
Los anagramas de la string S que cumplen las condiciones dadas son BACAY, BAYAC, CABAY, CAYAB, YABAC, YACAB.
Por lo tanto, el número total de tales anagramas es 6.

Enfoque ingenuo: el enfoque más simple es generar todos los anagramas posibles de la string dada y contar los anagramas que satisfacen la condición dada. Finalmente, imprima el conteo obtenido.
Complejidad temporal: O(N!*N)
Espacio auxiliar: O(1)

Enfoque eficiente: el enfoque anterior también se puede optimizar en función de las siguientes observaciones:

• Las strings que tienen el mismo número de consonantes y vocales satisfacen la condición dada.
• Las strings que tienen una consonante más que una vocal también satisfacen la condición dada.
• Aparte de estas dos condiciones, el recuento de posibles anagramas siempre será 0 .
• Ahora, el problema se puede resolver usando una fórmula combinatoria. Considere que hay C ₁ , C ₂ …, C _N consonantes y V ₁ , V ₂ , …, V _N vocales en la string S y   \sum C 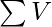 denota el número total de consonantes y vocales respectivamente, entonces la respuesta sería:

donde, 
C _i es la cuenta de i ^-ésima consonante.
_Vi es la cuenta de i ^-ésima vocal.

Siga los pasos a continuación para resolver el problema:

• Inicialice una variable, digamos respuesta , para almacenar el recuento total de anagramas.
• Almacene la frecuencia de cada carácter de la string S en un recuento de HashMap .
• Almacene el número de vocales y consonantes en S en las variables V y C respectivamente.
• Si el valor de V no es igual a C o C no es igual a (V + 1) , imprima 0 . De lo contrario, realizando los siguientes pasos:
  • Inicialice el denominador como 1 .
  • Recorra la string S usando la variable i y actualice el denominador como denominador*((count[S[i]])!) .
  • Inicializa el numerador a V!*C! y actualice el valor de la respuesta como numerador/denominador .
• Después de completar los pasos anteriores, imprima el valor de la respuesta como resultado.

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
#include <bits/stdc++.h>
 
#define ll long long
#define mod 1000000007
#define N 1000001
using namespace std;
 
// Function to compute factorials till N
void Precomputefact(unordered_map<ll, ll>& fac)
{
    ll ans = 1;
 
    // Iterate in the range [1, N]
    for (ll i = 1; i <= N; i++) {
 
        // Update ans to ans*i
        ans = (ans * i) % mod;
 
        // Store the value of ans
        // in fac[i]
        fac[i] = ans;
    }
    return;
}
 
// Function to check whether the
// current character is a vowel or not
bool isVowel(char a)
{
    if (a == 'A' || a == 'E' || a == 'I' || a == 'O'
        || a == 'U')
        return true;
    else
        return false;
}
 
// Function to count the number of
// anagrams of S satisfying the
// given condition
void countAnagrams(string s, int n)
{
    // Store the factorials upto N
    unordered_map<ll, ll> fac;
 
    // Function Call to generate
    // all factorials upto n
    Precomputefact(fac);
 
    // Create a hashmap to store
    // frequencies of all characters
    unordered_map<char, ll> count;
 
    // Store the count of
    // vowels and consonants
    int vo = 0, co = 0;
 
    // Iterate through all
    // characters in the string
    for (int i = 0; i < n; i++) {
 
        // Update the frequency
        // of current character
        count[s[i]]++;
 
        // Check if the character
        // is vowel or consonant
        if (isVowel(s[i]))
            vo++;
        else
            co++;
    }
 
    // Check if ΣC==ΣV+1 or ΣC==ΣV
    if ((co == vo + 1) || (co == vo)) {
 
        // Store the denominator
        ll deno = 1;
 
        // Calculate the denominator
        // of the expression
        for (auto c : count) {
 
            // Multiply denominator by factorial
            // of counts of all letters
            deno = (deno * fac[c.second]) % mod;
        }
 
        // Store the numerator
        ll nume = fac[co] % mod;
        nume = (nume * fac[vo]) % mod;
 
        // Store the answer by dividing
        // numerator by denominator
        ll ans = nume / deno;
 
        // Print the answer
        cout << ans;
    }
 
    // Otherwise, print 0
    else {
        cout << 0;
    }
}
 
// Driver Code
int main()
{
    string S = "GADO";
    int l = S.size();
    countAnagrams(S, l);
 
    return 0;
}

# Python 3 program for the above approach
#include <bits/stdc++.h>
 
mod = 1000000007
N = 1000001
 
fac = {}
 
# Function to compute factorials till N
def Precomputefact():
    global fac
    ans = 1
 
    # Iterate in the range [1, N]
    for i in range(1,N+1,1):
        # Update ans to ans*i
        ans = (ans * i) % mod
 
        # Store the value of ans
        # in fac[i]
        fac[i] = ans
 
    return
 
# Function to check whether the
# current character is a vowel or not
def isVowel(a):
    if (a == 'A' or a == 'E' or a == 'I' or a == 'O' or a == 'U'):
        return True
    else:
        return False
 
# Function to count the number of
# anagrams of S satisfying the
# given condition
def countAnagrams(s,n):
    # Store the factorials upto N
    global fac
 
    # Function Call to generate
    # all factorials upto n
    Precomputefact()
 
    # Create a hashmap to store
    # frequencies of all characters
    count = {}
 
    # Store the count of
    # vowels and consonants
    vo = 0
    co = 0
 
    # Iterate through all
    # characters in the string
    for i in range(n):
        # Update the frequency
        # of current character
        if s[i] in count:
            count[s[i]] += 1
        else:
            count[s[i]] = 1
 
        # Check if the character
        # is vowel or consonant
        if (isVowel(s[i])):
            vo += 1
        else:
            co += 1
 
    # Check if ΣC==ΣV+1 or ΣC==ΣV
    if ((co == vo + 1) or (co == vo)):
        # Store the denominator
        deno = 1
 
        # Calculate the denominator
        # of the expression
        for key,value in count.items():
            # Multiply denominator by factorial
            # of counts of all letters
            deno = (deno * fac[value]) % mod
 
        # Store the numerator
        nume = fac[co] % mod
        nume = (nume * fac[vo]) % mod
 
        # Store the answer by dividing
        # numerator by denominator
        ans = nume // deno
 
        # Print the answer
        print(ans)
 
    # Otherwise, print 0
    else:
        print(0)
 
# Driver Code
if __name__ == '__main__':
    S = "GADO"
    l = len(S)
    countAnagrams(S, l)
     
    # This code is contributed by ipg2016107.

4

Complejidad temporal: O(N)
Espacio auxiliar: O(N)