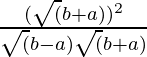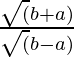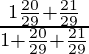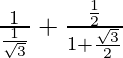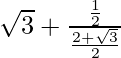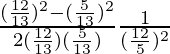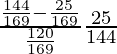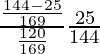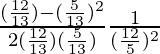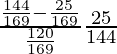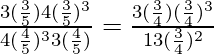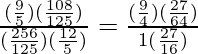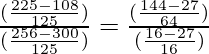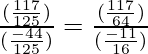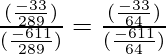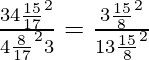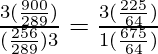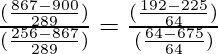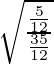Clase 10 Soluciones RD Sharma – Capítulo 5 Razones trigonométricas – Ejercicio 5.1

Pregunta 22. Si sinθ = a/b, encuentre secθ + tanθ en términos de a y b.

Solución:

Dado:

senθ = a/b

Del teorema de Pitágoras,

CA ² = BC ² + AB ²

segundo ² = un ² + AB ²

AB2 = ^_ $\sqrt{(b^2-a^2)}$

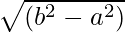
Ahora,

= secθ + tanθ

= $\frac{b}{\sqrt(b^2-a^2)}+\frac{a}{\sqrt(b^2-a^2)}$

= $\frac{b+a}{\sqrt(b^2-a^2)}$

= $\frac{(\sqrt(b+a))^2}{\sqrt(b-a)\sqrt(b+a)}$

= $\frac{\sqrt(b+a)}{\sqrt(b-a)}$

= $\sqrt\frac{b+a}{b-a}$

Pregunta 23. Si 8tanA = 15, encuentra sen A − cos A.

Solución:

Dado:

8tanA = 15

tanA = 15/8

Del teorema de Pitágoras,

CA ² = BC ² + AB ²

CA ² = 15 ² + 8 ²

CA ² = 225 + 64 = 289

CA = 17

Ahora,

= sen A − cos A

= 15/17 – 8/17

= (15 – 8)/17

= 7/17

Pregunta 24. Si tanθ = 20/21, demuestre que 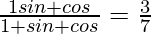$\frac{1−sinθ+cosθ}{1+sinθ+cosθ}=\frac{3}{7}$ .

Solución:

Dado: tanθ = 20/21

Del teorema de Pitágoras,

CA ² = BC ² + AB ²

CA ² = 20 ² + 21 ²

CA ² = 400 + 441 = 841

CA = 29

Ahora, tomando LHS

= $\frac{1−sinθ+cosθ}{1+sinθ+cosθ}$

= $\frac{1−\frac{20}{29}+\frac{21}{29}}{1+\frac{20}{29}+\frac{21}{29}}$

= $\frac{29-20+21}{29+20+21}$

= 30/70

= 3/7

Pregunta 25. Si cosec A = 2, encuentra el valor de 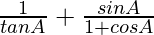$\frac{1}{tanA}+\frac{sinA}{1+cosA}$ .

Solución:

Dado:

cosec A = 2

Sabemos

sen A = 1/cosecA = 1/2

Y, sen 30° = 1/2

A = 30°

tan30° = 1/√3 y cos30° = √3/2

Ahora,

= $\frac{1}{tanA}+\frac{sinA}{1+cosA}$

= $\frac{1}{\frac{1}{\sqrt3}}+\frac{\frac{1}{2}}{1+\frac{\sqrt3}{2}}$

= $\sqrt3+\frac{\frac{1}{2}}{\frac{2+\sqrt3}{2}}$

= $\sqrt3+\frac{1}{2+\sqrt3}$

= $\frac{2\sqrt3+3+1}{2+\sqrt3}$
= $\frac{2\sqrt3+4}{2+\sqrt3}$

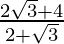
= 2

Pregunta 26. Si ∠A y ∠B son ángulos agudos tales que cos A = cos B, entonces demuestra que ∠A = ∠B.

Solución:

Consideremos un △ABC

De la figura,

Dado,

cos A = cos B

AC/AB = BC/AB

Multiplicando ambos lados por AB

(AC/AB) × AB = (BC/AB) × AB

CA = BC

En △ABC, AC = BC Entonces podemos decir que el triángulo es un triángulo isósceles,

y en un triangulo isosceles sabemos que si dos lados de un triangulo son iguales,

entonces el ángulo opuesto a los lados son iguales.

Por lo tanto, ∠A =∠B

Pregunta 27. En un Δ ABC, en ángulo recto en A, si tanC = √3, encuentra el valor de sen B cos C+ cos B sen C.

Solución:

En ángulo recto Δ ABC,

Dado: tan C = √3

∴AB = √3 y AC = 1

Del teorema de Pitágoras,

BC ² = AB ² + AC ²

BC ² = (√3) ² + 1 ²

BC ² = 3 + 1 = 4

BC = 2

Por lo tanto,

sen B cos C+ cos B sen C

= (1/2)(√3/2) + (√3/2)(√3/2)

= 1/4 + 3/4

= 4/4

= 1

Pregunta 28. Indique si las siguientes son verdaderas o falsas. Justifica tu respuesta.

(i) El valor de tan A es siempre menor que 1.

Solución:

FALSO. El valor de tan A no siempre es menor que 1.

Considere el triplete pitagórico, 13, 12 y 5

donde, 13 es la hipotenusa

Sabemos

tan A = Perpendicular/Base

Sea Perpendicular = 12 y Base = 5

entonces, tanA = 12/5 = 2.4 que es mayor que 1.

(ii) sec A = 12/5 para algún valor del ángulo A.

Solución:

CIERTO

Tenemos sec A = 12/5 para algún valor de ∠A

secθ = Hipotenusa/Base

En un triángulo rectángulo, la hipotenusa es el lado mayor.

Entonces secθ > 1 es válido

Aquí, secθ = 12/5

(iii) cos A es la abreviatura utilizada para la cosecante del ángulo A.

Solución:

FALSO

cos A significa coseno de ∠A

cos A = Base/Hipotenusa

Sin embargo,

cosec A = hipotenusa/perpendicular

(iv) cot A es el producto de cot y A.

Solución:

FALSO

cot A significa Cotangente de ∠A

cuna A = 1/tanA

Sólo “cuna” no define nada.

Por lo tanto, cot A no es el producto de cot y A.

(v) senθ = 4/3 para algún ángulo θ.

Solución:

FALSO

sinθ = 4/3 para algún valor de ∠θ

Tenemos,

sinθ = Perpendicular/Hipotenusa

En un triángulo rectángulo, la hipotenusa es el lado mayor.

Entonces senθ es siempre menor que 1.

Aquí, sinθ = 4/3 = 1.3 que es mayor que 1

Pregunta 29. Si senθ = 12/13, encuentra el valor de 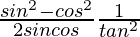$\frac{sen^2θ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$ .

Solución:

Dado:

senθ = 12/13

Usando el teorema de Pitágoras,

CA ² = BC ² + AB ²

13 ² = 12 ² + AB ²

AB2 ⁼ 169 − 144 = 25

AB = 5

= $\frac{sen^2θ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$

= $\frac{(\frac{12}{13})^2-(\frac{5}{13})^2}{2(\frac{12}{13})(\frac{5}{13} )}×\frac{1}{(\frac{12}{5})^2}$

= $\frac{\frac{144}{169}-\frac{25}{169}}{\frac{120}{169}}×\frac{25}{144}$

= $\frac{\frac{144-25}{169}}{\frac{120}{169}}×\frac{25}{144}$

= $\frac{119}{120}×\frac{25}{144}$

= 595/3456

Pregunta 30. Si cosθ = 5/13, encuentra el valor de 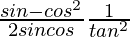$\frac{senθ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$ .

Solución:

Dado:

cosθ = 5/13

Usando el teorema de Pitágoras,

CA ² = BC ² + AB ²

13 ² = BC ² + 52

² aC = 169 − 25 = 144

BC = 12

= $\frac{senθ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$

= $\frac{(\frac{12}{13})-(\frac{5}{13})^2}{2(\frac{12}{13})(\frac{5}{13})} ×\frac{1}{(\frac{12}{5})^2}$

= $\frac{\frac{144}{169}-\frac{25}{169}}{\frac{120}{169}}×\frac{25}{144}$

= $\frac{\frac{144-25}{169}}{\frac{120}{169}}×\frac{25}{144}$

= $\frac{119}{120}×\frac{25}{144}$

= 595/3456

Pregunta 31. Si secA = 5/4, verifica que 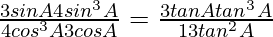$\frac{3sinA−4sin^3A }{4cos^3A−3cosA}=\frac{3tanA−tan^3A}{1−3tan^2A}$ .

Solución:

Dado:

segA = 5/4

Del teorema de Pitágoras,

CA ² = BC ² + AB ²

5 ² = BC ² + 4 ²

BC ² = 25 − 16 = 9

BC = 3

Ahora

= $\frac{3sinA−4sin^3A }{4cos^3A−3cosA}=\frac{3tanA−tan^3A}{1−3tan^2A}$

= $\frac{3(\frac{3}{5})−4(\frac{3}{5})^3 }{4(\frac{4}{5})^3−3(\frac{4}{5})}=\frac{3(\frac{3}{4})−(\frac{3}{4})^3}{1−3(\frac{3}{4})^2}$

= $\frac{(\frac{9}{5})−(\frac{108}{125}) }{(\frac{256}{125})−(\frac{12}{5})}=\frac{(\frac{9}{4})−(\frac{27}{64})}{1−(\frac{27}{16})}$

= $\frac{(\frac{225-108}{125}) }{(\frac{256-300}{125})}=\frac{(\frac{144-27}{64})}{(\frac{16-27}{16})}$

= $\frac{(\frac{117}{125}) }{(\frac{-44}{125})}=\frac{(\frac{117}{64})}{(\frac{-11}{16})}$

= 117/-44 = 117/(11(4))

= 117/-44 = 117/-44

Por lo tanto probado

Pregunta 32. Si senθ = 3/4, prueba que 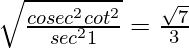$\sqrt\frac{cosec^2θ−cot^2θ}{sec^2θ−1}=\frac{\sqrt 7}{3}$ .

Solución:

Dado: senθ = 3/4

Del teorema de Pitágoras,

CA ² = BC ² + AB ²

4 ² = AB ² + 3 ²

AB ² = 16 – 9 = 7

AB =√7

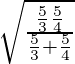
Tenemos,

$\sqrt\frac{cosec^2θ−cot^2θ}{sec^2θ−1}=\frac{\sqrt 7}{3}$

Ahora cuadrando ambos lados

= $(\sqrt\frac{cosec^2θ−cot^2θ}{sec^2θ−1})^2=(\frac{\sqrt 7}{3})^2$

= $\frac{cosec^2θ−cot^2θ}{sec^2θ−1}$

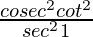
= 7/9

Sabemos

1 + cuna ² θ = cosec ² θ

1 + bronceado ² θ = segundo ² θ

= 1/bronceado ² θ = 7/9

= $\frac{1}{(\frac{3}{\sqrt7})^2}=\frac{7}{9}$

= 7/9 = 7/9

Por lo tanto probado

Pregunta 33. Si secA = 17/8, verifica que 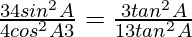$\frac{3−4sin^2A}{4cos^2A−3}=\frac{3−tan^2A}{1−3tan^2A}$ .

Solución:

Dado: secA = 17/8

Del teorema de Pitágoras,

CA ² = BC ² + AB ²

17 ² = BC ² + 8 ²

² aC = 289 − 64 = 225

BC = 15 $\frac{(\frac{-33}{289})}{(\frac{-611}{289})}=\frac{(\frac{-33}{64})}{(\frac{-611}{64})}$

Tenemos

$\frac{3−4sin^2A}{4cos^2A−3}=\frac{3−tan^2A}{1−3tan^2A}$

Poniendo los valores de sinA, cosA y tanA en la ecuación anterior

= $\frac{3−4\frac{15}{17}^2}{4\frac{8}{17}^2−3}=\frac{3−\frac{15}{8}^2}{1−3\frac{15}{8}^2}$

= $\frac{3−(\frac{900}{289})}{(\frac{256}{289})−3}=\frac{3−(\frac{225}{64})}{1−(\frac{675}{64})}$

= $\frac{(\frac{867-900}{289})}{(\frac{256-867}{289})}=\frac{(\frac{192-225}{64})}{(\frac{64-675}{64})}$

= $\frac{(\frac{-33}{289})}{(\frac{-611}{289})}=\frac{(\frac{-33}{64})}{(\frac{-611}{64})}$

= 33/611 = 33/611

Por lo tanto probado

Pregunta 34. Si cotθ = 3/4, prueba que 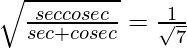$\sqrt\frac{secθ−cosecθ}{secθ+cosecθ}=\frac{1}{\sqrt 7}$ .

Solución:

Dado: cotθ = 3/4

tanθ = 4/3

Usando el teorema de Pitágoras

senθ = 4/5, cosθ = 3/5

cosecθ = 5/4, secθ = 5/3

Ahora, tomando LHS

= $\sqrt\frac{secθ−cosecθ}{secθ+cosecθ}$

= $\sqrt\frac{\frac{5}{3}−\frac{5}{4}}{\frac{5}{3}+\frac{5}{4}}$

= $\sqrt\frac{\frac{5}{12}}{\frac{35}{12}}$

= $\sqrt\frac{5}{35}$

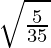
= 1/√7

Pregunta 35. Si 3cosθ − 4sinθ = 2cosθ + sinθ, entonces encuentra tanθ.

Solución:

Dado: 3cosθ − 4sinθ = 2cosθ + sinθ

Dividiendo ambas ecuaciones por cosθ obtenemos,

$3\frac{cosθ}{cosθ}−4\frac{sinθ}{cosθ}=2\frac{cosθ}{cosθ}+\frac{sinθ}{cosθ}$

3 – 4tanθ = 2 + tanθ

3 – 2 = 4tanθ + tanθ

tanθ = 1/5

Pregunta 36. Si ∠A y ∠B son ángulos agudos tales que tan A = tan B, entonces demuestra que ∠A = ∠B.

Solución:

Consideremos un △ABC

De la figura,

Dado:

bronceado A = bronceado B

BC/CA = CA/BC

CA ² = BC ²

CA = BC

En △ABC, AC = BC Entonces podemos decir que el triángulo es un triángulo isósceles, √3

y en un triangulo isosceles sabemos que si dos lados de un triangulo son iguales,

entonces el ángulo opuesto a los lados son iguales.

Por lo tanto ∠A =∠B

Publicación traducida automáticamente

Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 10 Soluciones RD Sharma – Capítulo 5 Razones trigonométricas – Ejercicio 5.1 | conjunto 3

Pregunta 22. Si sinθ = a/b, encuentre secθ + tanθ en términos de a y b.

Pregunta 23. Si 8tanA = 15, encuentra sen A − cos A.

Pregunta 24. Si tanθ = 20/21, demuestre que $\frac{1−sinθ+cosθ}{1+sinθ+cosθ}=\frac{3}{7}$ .

Pregunta 25. Si cosec A = 2, encuentra el valor de $\frac{1}{tanA}+\frac{sinA}{1+cosA}$ .

Pregunta 26. Si ∠A y ∠B son ángulos agudos tales que cos A = cos B, entonces demuestra que ∠A = ∠B.

Pregunta 27. En un Δ ABC, en ángulo recto en A, si tanC = √3, encuentra el valor de sen B cos C+ cos B sen C.

Pregunta 28. Indique si las siguientes son verdaderas o falsas. Justifica tu respuesta.

(i) El valor de tan A es siempre menor que 1.

(ii) sec A = 12/5 para algún valor del ángulo A.

(iii) cos A es la abreviatura utilizada para la cosecante del ángulo A.

(iv) cot A es el producto de cot y A.

(v) senθ = 4/3 para algún ángulo θ.

Pregunta 29. Si senθ = 12/13, encuentra el valor de $\frac{sen^2θ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$ .

Pregunta 30. Si cosθ = 5/13, encuentra el valor de $\frac{senθ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$ .

Pregunta 31. Si secA = 5/4, verifica que $\frac{3sinA−4sin^3A }{4cos^3A−3cosA}=\frac{3tanA−tan^3A}{1−3tan^2A}$ .

Pregunta 32. Si senθ = 3/4, prueba que $\sqrt\frac{cosec^2θ−cot^2θ}{sec^2θ−1}=\frac{\sqrt 7}{3}$ .

Pregunta 33. Si secA = 17/8, verifica que $\frac{3−4sin^2A}{4cos^2A−3}=\frac{3−tan^2A}{1−3tan^2A}$ .

Pregunta 34. Si cotθ = 3/4, prueba que $\sqrt\frac{secθ−cosecθ}{secθ+cosecθ}=\frac{1}{\sqrt 7}$ .

Pregunta 35. Si 3cosθ − 4sinθ = 2cosθ + sinθ, entonces encuentra tanθ.

Pregunta 36. Si ∠A y ∠B son ángulos agudos tales que tan A = tan B, entonces demuestra que ∠A = ∠B.

Deja una respuesta Cancelar la respuesta

Pregunta 22. Si sinθ = a/b, encuentre secθ + tanθ en términos de a y b.

Pregunta 23. Si 8tanA = 15, encuentra sen A − cos A.

Pregunta 24. Si tanθ = 20/21, demuestre que .

Pregunta 25. Si cosec A = 2, encuentra el valor de .

Pregunta 26. Si ∠A y ∠B son ángulos agudos tales que cos A = cos B, entonces demuestra que ∠A = ∠B.

Pregunta 27. En un Δ ABC, en ángulo recto en A, si tanC = √3, encuentra el valor de sen B cos C+ cos B sen C.

Pregunta 28. Indique si las siguientes son verdaderas o falsas. Justifica tu respuesta.

(i) El valor de tan A es siempre menor que 1.

(ii) sec A = 12/5 para algún valor del ángulo A.

(iii) cos A es la abreviatura utilizada para la cosecante del ángulo A.

(iv) cot A es el producto de cot y A.

(v) senθ = 4/3 para algún ángulo θ.

Pregunta 29. Si senθ = 12/13, encuentra el valor de .

Pregunta 30. Si cosθ = 5/13, encuentra el valor de .

Pregunta 31. Si secA = 5/4, verifica que .

Pregunta 32. Si senθ = 3/4, prueba que .

Pregunta 33. Si secA = 17/8, verifica que .

Pregunta 34. Si cotθ = 3/4, prueba que .

Pregunta 35. Si 3cosθ − 4sinθ = 2cosθ + sinθ, entonces encuentra tanθ.

Pregunta 36. Si ∠A y ∠B son ángulos agudos tales que tan A = tan B, entonces demuestra que ∠A = ∠B.

Deja una respuesta Cancelar la respuesta

Pregunta 24. Si tanθ = 20/21, demuestre que $\frac{1−sinθ+cosθ}{1+sinθ+cosθ}=\frac{3}{7}$ .

Pregunta 25. Si cosec A = 2, encuentra el valor de $\frac{1}{tanA}+\frac{sinA}{1+cosA}$ .

Pregunta 29. Si senθ = 12/13, encuentra el valor de $\frac{sen^2θ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$ .

Pregunta 30. Si cosθ = 5/13, encuentra el valor de $\frac{senθ-cos^2θ}{2sinθcosθ}×\frac{1}{tan^2θ}$ .

Pregunta 31. Si secA = 5/4, verifica que $\frac{3sinA−4sin^3A }{4cos^3A−3cosA}=\frac{3tanA−tan^3A}{1−3tan^2A}$ .

Pregunta 32. Si senθ = 3/4, prueba que $\sqrt\frac{cosec^2θ−cot^2θ}{sec^2θ−1}=\frac{\sqrt 7}{3}$ .

Pregunta 33. Si secA = 17/8, verifica que $\frac{3−4sin^2A}{4cos^2A−3}=\frac{3−tan^2A}{1−3tan^2A}$ .

Pregunta 34. Si cotθ = 3/4, prueba que $\sqrt\frac{secθ−cosecθ}{secθ+cosecθ}=\frac{1}{\sqrt 7}$ .