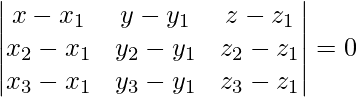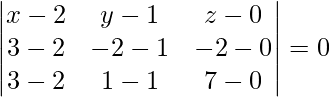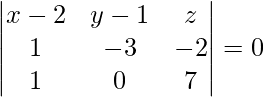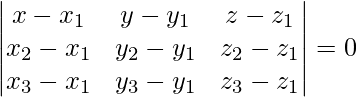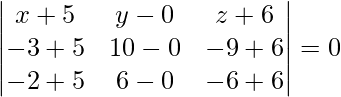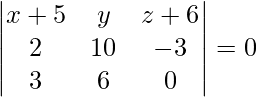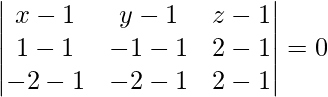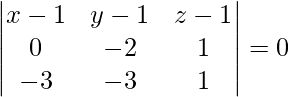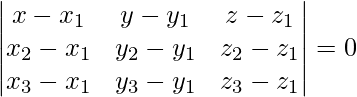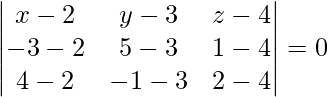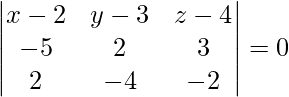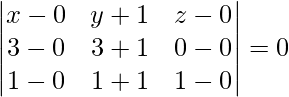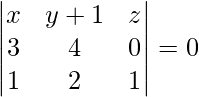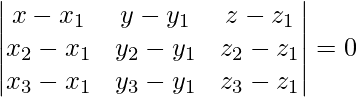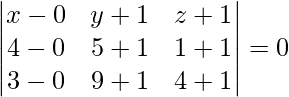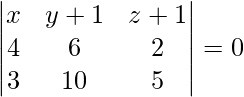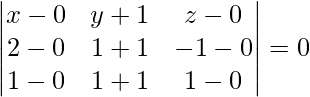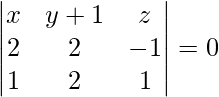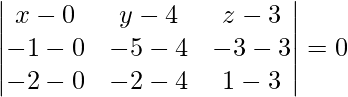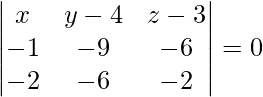Clase 12 RD Sharma Solutions – Capítulo 29 El avión – Ejercicio 29.1 – Part 3

Pregunta 1(i). Encuentra la ecuación del plano que pasa por los siguientes puntos (2, 1, 0), (3, -2, -2) y (3, 1, 7).

Solución:

Los puntos dados son (2, 1, 0), (3, -2, -2) y (3, 1, 7)

La ecuación del plano que pasa por tres puntos viene dada por

$\begin{vmatrix} x-x_1&y-y_1&z-z_1\\ x_2-x_1&y_2-y_1&z_2-z_1\\ x_3-x_1&y_3-y_1&z_3-z_1\\ \end{vmatrix} = 0$

$\begin{vmatrix} x-2&y-1&z-0\\ 3-2&-2-1&-2-0\\ 3-2&1-1&7-0\\ \end{vmatrix} = 0$

$\begin{vmatrix} x-2&y-1&z\\ 1&-3&-2\\ 1&0&7\\ \end{vmatrix} = 0$

= (x – 2)(-21 – 0) – (y – 1)(7 + 2) + z(0 + 3) = 0

= -21x + 42 – 9y + 9 + 3z = 0

= -21x – 9y + 3z + 51 = 0

Tomando -3 como común, obtenemos la ecuación resultante del plano

7x + 3y – z – 17 = 0

Pregunta 1(ii). Encuentra la ecuación del plano que pasa por los siguientes puntos (-5, 0, 6), (-3, 10, -9) y (-2, 6, -6).

Solución:

Los puntos dados son (-5, 0, 6), (-3, 10, -9) y (-2, 6, -6).

La ecuación de un plano que pasa por tres puntos viene dada por

$\begin{vmatrix} x-x_1&y-y_1&z-z_1\\ x_2-x_1&y_2-y_1&z_2-z_1\\ x_3-x_1&y_3-y_1&z_3-z_1\\ \end{vmatrix} = 0$

$\begin{vmatrix} x+5&y-0&z+6\\ -3+5&10-0&-9+6\\ -2+5&6-0&-6+6\\ \end{vmatrix} = 0$

$\begin{vmatrix} x+5&y&z+6\\ 2&10&-3\\ 3&6&0\\ \end{vmatrix} = 0$

(x + 5)(0 + 18) – y(0 + 9) + (z + 6)(12 – 30) = 0

(x + 5)(18) – y(9) + (z + 6)(-18) = 0

18x + 90 – 9y – 18z -108 = 0

Tomando 9 como común, obtenemos la ecuación

2x-y-2z-2 = 0

Pregunta 1(iii). Encuentra la ecuación del plano que pasa por los siguientes puntos (1, 1, 1), (1, -1, 2) y (-2, -2, 2).

Solución:

Dados tres puntos son (1, 1, 1), (1, -1, 2) y (-2, -2, 2)

La ecuación del plano que pasa por tres puntos viene dada por

$\begin{vmatrix} x-x_1&y-y_1&z-z_1\\ x_2-x_1&y_2-y_1&z_2-z_1\\ x_3-x_1&y_3-y_1&z_3-z_1\\ \end{vmatrix} = 0$

$\begin{vmatrix} x-1&y-1&z-1\\ 1-1&-1-1&2-1\\ -2-1&-2-1&2-1\\ \end{vmatrix} = 0$

$\begin{vmatrix} x-1&y-1&z-1\\ 0&-2&1\\ -3&-3&1\\ \end{vmatrix} = 0$

(x – 1)(-2 + 3) – (y – 1)(0 + 3) + (z – 1)(0 – 6) = 0

(x – 1)(1) – (y – 1)(3) + (z – 1)(-6) = 0

x – 1 – 3y + 3 – 6z + 6 = 0

x -3y – 6z + 8 = 0

Pregunta 1(iv). Encuentra la ecuación del plano que pasa por los siguientes puntos (2, 3, 4), (-3, 5, 1) y (4, -1, 2).

Solución:

Los puntos dados son (2, 3, 4), (-3, 5, 1) y (4, -1, 2).

La ecuación del plano que pasa por tres puntos viene dada por

$\begin{vmatrix} x-x_1&y-y_1&z-z_1\\ x_2-x_1&y_2-y_1&z_2-z_1\\ x_3-x_1&y_3-y_1&z_3-z_1\\ \end{vmatrix} = 0$

$\begin{vmatrix} x-2&y-3&z-4\\ -3-2&5-3&1-4\\ 4-2&-1-3&2-4\\ \end{vmatrix} = 0$

$\begin{vmatrix} x-2&y-3&z-4\\ -5&2&3\\ 2&-4&-2\\ \end{vmatrix} = 0$

(x – 2)(-4 – 12) – (y – 3)(10 + 6) + (z – 4)(20 – 4) = 0

(x – 2)(-16) – (y – 3)(16) + (z – 4)(16) = 0

-16x – 32 – 16y + 48 + 16z – 64 = 0

-16x – 16y + 16z + 16 = 0

Tomando -16 común obtenemos la ecuación del plano como,

x + y – z – 1 = 0

Pregunta 1(v). Encuentra la ecuación del plano que pasa por los siguientes puntos (0, -1, 0), (3, 3, 0) y (1, 1, 1).

Solución:

Los puntos dados son (0, -1, 0), (3, 3, 0) y (1, 1, 1)

La ecuación del plano que pasa por tres puntos viene dada por,

$\begin{vmatrix} x-x_1&y-y_1&z-z_1\\ x_2-x_1&y_2-y_1&z_2-z_1\\ x_3-x_1&y_3-y_1&z_3-z_1\\ \end{vmatrix} = 0$

$\begin{vmatrix} x-0&y+1&z-0\\ 3-0&3+1&0-0\\ 1-0&1+1&1-0\\ \end{vmatrix} = 0$

$\begin{vmatrix} x&y+1&z\\ 3&4&0\\ 1&2&1\\ \end{vmatrix} = 0$

x(4 – 0) – (y + 1)(3 – 0) + z(6 – 4) = 0

4x – (y + 1)(3) + z(2) = 0

4x – 3y – 3 + 2z = 0

4x – 3y + 2z – 3 = 0

Pregunta 2. Muestre que los cuatro puntos (0, -1, 1), (4, 5, 1), (3, 9, 4) y (-4, 4, 4) son coplanares y encuentre la ecuación de la plano común.

Solución:

Para demostrar que los puntos dados (0, -1, 1), (4, 5, 1), (3, 9, 4) y (-4, 4, 4) son coplanares.

La solución eficiente es encontrar la ecuación del plano que pasa por tres puntos cualesquiera.

Luego sustituya el cuarto punto en la ecuación resultante.

Si se cumple, entonces los cuatro puntos son coplanares.

La ecuación del plano que pasa por tres puntos (0, -1, 1), (4, 5, 1) y (3, 9, 4) viene dada por

$\begin{vmatrix} x-x_1&y-y_1&z-z_1\\ x_2-x_1&y_2-y_1&z_2-z_1\\ x_3-x_1&y_3-y_1&z_3-z_1\\ \end{vmatrix} = 0$

$\begin{vmatrix} x-0&y+1&z+1\\ 4-0&5+1&1+1\\ 3-0&9+1&4+1\\ \end{vmatrix} = 0$

$\begin{vmatrix} x&y+1&z+1\\ 4&6&2\\ 3&10&5\\ \end{vmatrix} = 0$

x(30 – 20) – (y + 1)(20 – 6) + (z + 1)(40 – 18) = 0

10x – (y + 1)(14) + (z + 1)(22) = 0

10x – 14y + 22z + 8 = 0

Tomando 2 como común,

5x – 7y + 11z + 4 = 0 -Ecuación (1)

Sustituya el punto restante (-4, 4, 4) en la ecuación anterior (1)

5(-4) – 7(4) + 11(4) + 4 = 0

-48 + 48 = 0

0 = 0

LHS = RHS

Como el punto satisface la ecuación. Entonces, los cuatro puntos son coplanares.

La ecuación del plano común es 5x – 7y + 11z + 4 = 0

Pregunta 3(i). Demuestre que los siguientes puntos son coplanares (0, -1, 0), (2, 1, -1), (1, 1, 1) y (3, 3, 0).

Solución:

Los puntos dados son (0, -1, 0), (2, 1, -1), (1, 1, 1) y (3, 3, 0).

La ecuación del plano que pasa por tres puntos (0, -1, 0), (2, 1, -1), (1, 1, 1) viene dada por

$\begin{vmatrix} x-x_1&y-y_1&z-z_1\\ x_2-x_1&y_2-y_1&z_2-z_1\\ x_3-x_1&y_3-y_1&z_3-z_1\\ \end{vmatrix} = 0$

$\begin{vmatrix} x-0&y+1&z-0\\ 2-0&1+1&-1-0\\ 1-0&1+1&1-0\\ \end{vmatrix} = 0$

$\begin{vmatrix} x&y+1&z\\ 2&2&-1\\ 1&2&1\\ \end{vmatrix} = 0$

x(2 + 2) – (y + 1)(2 + 1) + z(4 – 2) = 0

x(4) – (y + 1)(3) + z(2) = 0

4x – 3y – 3 + 2z = 0

4x – 3y + 2z – 3 = 0 -Ecuación (1)

Sustituya el punto cuatro en la ecuación (1)

4(3) – 3(3) + 2 (0) – 3 = 0

12 – 9 + 0 – 3 = 0

12 – 12 = 0

0 = 0

LHS = RHS

Como cuarto punto satisface la ecuación.

Entonces, los cuatro puntos son coplanares.

Pregunta 3(ii). Demuestre que los siguientes puntos son coplanares (0, 4, 3), (-1, -5, -3), (-2, -2, 1) y (1, 1, -1).

Solución:

Dados cuatro puntos son (0, 4, 3), (-1, -5, -3), (-2, -2, 1) y (1, 1, -1).

La ecuación de los puntos que pasan por tres puntos viene dada por

$\begin{vmatrix} x-x_1&y-y_1&z-z_1\\ x_2-x_1&y_2-y_1&z_2-z_1\\ x_3-x_1&y_3-y_1&z_3-z_1\\ \end{vmatrix} = 0$

$\begin{vmatrix} x-0&y-4&z-3\\ -1-0&-5-4&-3-3\\ -2-0&-2-4&1-3\\ \end{vmatrix} = 0$

$\begin{vmatrix} x&y-4&z-3\\ -1&-9&-6\\ -2&-6&-2\\ \end{vmatrix} = 0$

x(18 – 36) – (y – 4)(2 – 12) + (z – 3)(6 – 18) = 0

x(-18) – (y – 4)(-10) + (z – 3)(-12) = 0

-18x + 10y – 40 – 12z + 36 = 0

-18x + 10y – 12z – 4 = 0 -Ecuación (1)

Sustituir el cuarto punto en la ecuación (1)

-18(1) + 10(1) – 12(-1) – 4 = 0

-18 +10 +12 -4 = 0

-22 + 22 = 0

0 = 0

LHS = RHS

Como el cuarto punto satisface la ecuación dada.

Entonces, los cuatro puntos son coplanares.

Publicación traducida automáticamente

Artículo escrito por vishnuteja476 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1(i). Encuentra la ecuación del plano que pasa por los siguientes puntos (2, 1, 0), (3, -2, -2) y (3, 1, 7).

Pregunta 1(ii). Encuentra la ecuación del plano que pasa por los siguientes puntos (-5, 0, 6), (-3, 10, -9) y (-2, 6, -6).

Pregunta 1(iii). Encuentra la ecuación del plano que pasa por los siguientes puntos (1, 1, 1), (1, -1, 2) y (-2, -2, 2).

Pregunta 1(iv). Encuentra la ecuación del plano que pasa por los siguientes puntos (2, 3, 4), (-3, 5, 1) y (4, -1, 2).

Pregunta 1(v). Encuentra la ecuación del plano que pasa por los siguientes puntos (0, -1, 0), (3, 3, 0) y (1, 1, 1).

Pregunta 2. Muestre que los cuatro puntos (0, -1, 1), (4, 5, 1), (3, 9, 4) y (-4, 4, 4) son coplanares y encuentre la ecuación de la plano común.

Pregunta 3(i). Demuestre que los siguientes puntos son coplanares (0, -1, 0), (2, 1, -1), (1, 1, 1) y (3, 3, 0).

Pregunta 3(ii). Demuestre que los siguientes puntos son coplanares (0, 4, 3), (-1, -5, -3), (-2, -2, 1) y (1, 1, -1).

Deja una respuesta Cancelar la respuesta