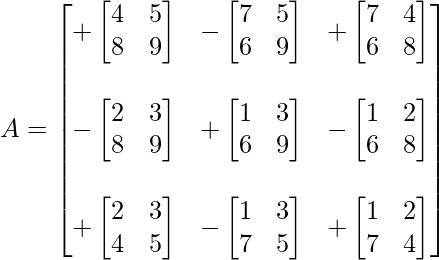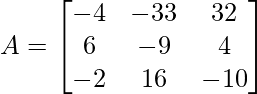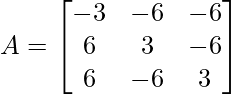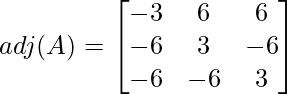Adjunto de una Array

El conocimiento de arrays es necesario para diversas ramas de las matemáticas. Las arrays son una de las herramientas más poderosas de las matemáticas. De las arrays vienen los Determinantes, ahora vemos una de las propiedades del Determinante en este artículo. En este artículo, vemos cómo encontrar el adjunto de una array. Para saber sobre el Adjunto de una Array tenemos que saber sobre el Cofactor de una array.

Cofactor de una array

El cofactor es el número que obtenemos cuando eliminamos la columna y la fila de un elemento designado en una array. Significa tomar un elemento de una array y eliminar toda la fila y la columna de ese elemento de la array, luego qué elementos presentes en esa array, que se denominan cofactor.

Ejemplo

Tomemos una array, $A =\begin{bmatrix} 1 & 2 & 3\\ 7 & 4 & 5 \\ 6 & 8 & 9 \end{bmatrix}$

Ahora encuentra el cofactor del elemento 3

Paso 1: elimine toda la fila y la columna que contiene el elemento 3

Paso 2: Tome los elementos presentes tal como están en la array después del Paso 1.

Entonces, el cofactor de 3 es $\begin{bmatrix} 7 & 4 \\ 6 & 8 \end{bmatrix}$

Para encontrar el adjunto de una array, primero tenemos que encontrar el cofactor de cada elemento y luego encontrar 2 pasos más. ver a continuación los pasos,

Paso 1: Encuentra el Cofactor de cada elemento presente en la array.
Paso 2: crea otra array con los cofactores y expande los cofactores, luego obtenemos una array
Paso 3: Ahora encuentre la transpuesta de la array que viene después del Paso 2.

Entendamos todo esto tomando algunos ejemplos.

Ejemplos

Ejemplo 1: ¿Encuentra el adjunto de la array dada 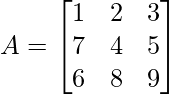$A =\begin{bmatrix} 1 & 2 & 3\\ 7 & 4 & 5 \\ 6 & 8 & 9 \end{bmatrix}$ ?

Solución:

Paso 1: Encontrar el cofactor de cada elemento

Para encontrar el cofactor de cada elemento, debemos eliminar la fila y la columna de cada elemento uno por uno y tomar los elementos presentes después de eliminar.

Cofactor del elemento en A[0,0] = 1 : $+\begin{bmatrix} 4 & 5 \\ 8 & 9 \end{bmatrix}$ = +(4×9 – 8×5) = -4

Cofactor de elementos en A[0,1] = 2 : $-\begin{bmatrix} 7 & 5 \\ 6 & 9 \end{bmatrix}$ = -(7×9 – 6×5) = -33

Cofactor de elementos en A[0,2] = 3 : $+\begin{bmatrix} 7 & 4 \\ 6 & 8 \end{bmatrix}$ = +(7×8 – 6×4) = 32

Cofactor de elementos en A[2,0] = 7 : $-\begin{bmatrix} 2 & 3 \\ 8 & 9 \end{bmatrix}$ = -(2×9 – 8×3) = 6

Cofactor de elementos en A[2,1] = 4 : $+\begin{bmatrix} 1 & 3 \\ 6 & 9 \end{bmatrix}$ = +(1×9 – 6×3) = -9

Cofactor de elementos en A[2,2] = 5 : $-\begin{bmatrix} 1 & 2 \\ 6 & 8 \end{bmatrix}$ = -(1×8 – 6×2) = 4

Cofactor de elementos en A[3,0] = 6 : $+\begin{bmatrix} 2 & 3 \\ 4 & 5 \end{bmatrix}$ = +(2×5 – 4×3) = -2

Cofactor de elementos en A[3,1] = 8 : $-\begin{bmatrix} 1 & 3 \\ 7 & 5 \end{bmatrix}$ = -(1×5 – 7×3) = 16

Cofactor de elementos en A[3,2] = 9 : $+\begin{bmatrix} 1 & 2 \\ 7 & 4 \end{bmatrix}$ = +(1×4 – 7×2) = -10

La array se ve así con los cofactores:

$A =\begin{bmatrix} +\begin{bmatrix} 4 & 5 \\ 8 & 9 \end{bmatrix} & -\begin{bmatrix} 7 & 5 \\ 6 & 9 \end{bmatrix} & +\begin{bmatrix} 7 & 4 \\ 6 & 8 \end{bmatrix}\\ \\ -\begin{bmatrix} 2 & 3 \\ 8 & 9 \end{bmatrix} & +\begin{bmatrix} 1 & 3 \\ 6 & 9 \end{bmatrix} & -\begin{bmatrix} 1 & 2 \\ 6 & 8 \end{bmatrix} \\ \\ +\begin{bmatrix} 2 & 3 \\ 4 & 5 \end{bmatrix} & -\begin{bmatrix} 1 & 3 \\ 7 & 5 \end{bmatrix} & +\begin{bmatrix} 1 & 2 \\ 7 & 4 \end{bmatrix} \end{bmatrix}$

La array final de cofactores:

$A =\begin{bmatrix} -4 & -33 & 32\\ 6 & -9 & 4 \\ -2 & 16 & -10 \end{bmatrix}$

Paso 2: Encuentra la transpuesta de la array obtenida en el paso 1

$adj(A) =\begin{bmatrix} -4 & 6 & -2\\ -33 & -9 & 16 \\ 32 & 4 & -10 \end{bmatrix}$

Este es el adjunto de la array.

Ejemplo 2: ¿Encuentra el adjunto de la array dada $A =\begin{bmatrix} -1 & -2 & -2\\ 2 & 1 & -2 \\ 2 & -2 & 1 \end{bmatrix}$ ?

Solución:

Paso 1: Encontrar el cofactor de cada elemento

Para encontrar el cofactor de cada elemento, debemos eliminar la fila y la columna de cada elemento uno por uno y tomar los elementos presentes después de eliminar.

Cofactor del elemento en A[0,0] = -1 : $+\begin{bmatrix} 1 & -2 \\ -2 & 1 \end{bmatrix}$ = +(1×1 – (-2)x(-2)) = -3

Cofactor de elementos en A[0,1] = -2 : $-\begin{bmatrix} 2 & -2 \\ 2 & 1 \end{bmatrix}$ = -(2×1 – 2x(-2)) = -6

Cofactor de elementos en A[0,2] = -2 : $+\begin{bmatrix} 2 & 1 \\ 2 & -2 \end{bmatrix}$ = +(2x(-2) – 2×1) = -6

Cofactor de elementos en A[2,0] = 2 : $-\begin{bmatrix} -2 & -2 \\ -2 & 1 \end{bmatrix}$ = -((-2)x1 – (-2)x(-2)) = 6

Cofactor de elementos en A[2,1] = 1 : $+\begin{bmatrix} -1 & -2 \\ 2 & 1 \end{bmatrix}$ = +((-1)x1 – 2x(-2)) = 3

Cofactor de elementos en A[2,2] = -2 : $-\begin{bmatrix} -1 & -2 \\ 2 & -2 \end{bmatrix}$ = -((-1)x(-2) – 2x(-2)) = -6

Cofactor de elementos en A[3,0] = 2 : $+\begin{bmatrix} -2 & -2 \\ 1 & -2 \end{bmatrix}$ = +((-2)x(-2) – 1x(-2)) = 6

Cofactor de elementos en A[3,1] = -2 : $-\begin{bmatrix} -1 & -2 \\ 2 & -2 \end{bmatrix}$ = -((-1)x(-2) – 2x(-2)) = -6

Cofactor de elementos en A[3,2] = 1 : $+\begin{bmatrix} -1 & -2 \\ 2 & 1 \end{bmatrix}$ = +((-1)x(-1)- 2x(-2)) = 3

La array final de cofactores:

$A =\begin{bmatrix} -3 & -6 & -6\\ 6 & 3 & -6 \\ 6 & -6 & 3 \end{bmatrix}$

Paso 2: Encuentra la transpuesta de la array obtenida en el Paso 1

$adj(A) =\begin{bmatrix} -3 & 6 & 6\\ -6 & 3 & -6 \\ -6 & -6 & 3 \end{bmatrix}$

Este es el adjunto de la array.

Array singular

Se dice que una array es una array singular si el determinante de esa array es CERO. Esta singularidad se logra solo con arrays cuadradas porque solo las arrays cuadradas tienen determinante. Además, la inversión de arrays singulares no es posible porque para encontrar la inversa de una array necesitamos dividir el adjunto de una array con el determinante de la array, pero para una array singular, el valor del determinante es CERO. Entonces la división no es posible aquí. Para encontrar una array es singular o no hay alguna regla, ver a continuación:

Regla 1: Primero verifica si la array es cuadrada o no.
Regla 2: Si es cuadrado, calcula su determinante y verifica si el valor es CERO o no. Si es CERO entonces es una array singular.

Ejemplos

Ejemplo 1: Comprobar si la array dada es singular o no, 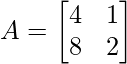$A =\begin{bmatrix} 4 & 1\\ 8 & 2\end{bmatrix}$ ?

Solución:

Aquí esta array es una array cuadrada, así que encontremos el determinante de esta array,

det A = (4×2 – 8×1) = 0

Aquí el determinante de A es CERO,

También $\frac{Adj(A)}{det (A)} = \frac{Adj(A)}{0} = \infty$ = inversión no posible

Entonces podemos decir que la array A es una array singular.

Ejemplo 2: Comprobar si la array dada es singular o no, $A =\begin{bmatrix} 2 & 4 & 6\\ 2 & 0 & 2 \\ 6 & 8 & 14 \end{bmatrix}$ ?

Solución:

det(A) = 2(0 – 16) – 4(28 – 12) + 6(16 – 0) [usando la primera fila]

= −2(16) + 2(16) = 0

Aquí el determinante de A es CERO

También $\frac{Adj(A)}{det (A)} = \frac{Adj(A)}{0} = \infty$ = inversión no posible

Entonces podemos decir que la array A es una array singular.

Propiedades de la array singular

Toda array singular tiene su determinante valor CERO.
Toda array singular debe ser de array cuadrada.
Toda la array singular no se puede invertir.
No hay inversa multiplicativa para una array singular.

Publicación traducida automáticamente

Artículo escrito por SoumikMondal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Cofactor de una array

Ejemplo