factor primo

El factor primo es el factor del número dado que es un número primo . Los factores son los números que se multiplican para obtener otro número. En palabras simples, el factor primo es encontrar qué números primos se multiplican para formar el número original.

Ejemplo: Los factores primos de 15 son 3 y 5 (porque 3×5=15, y 3 y 5 son números primos). 

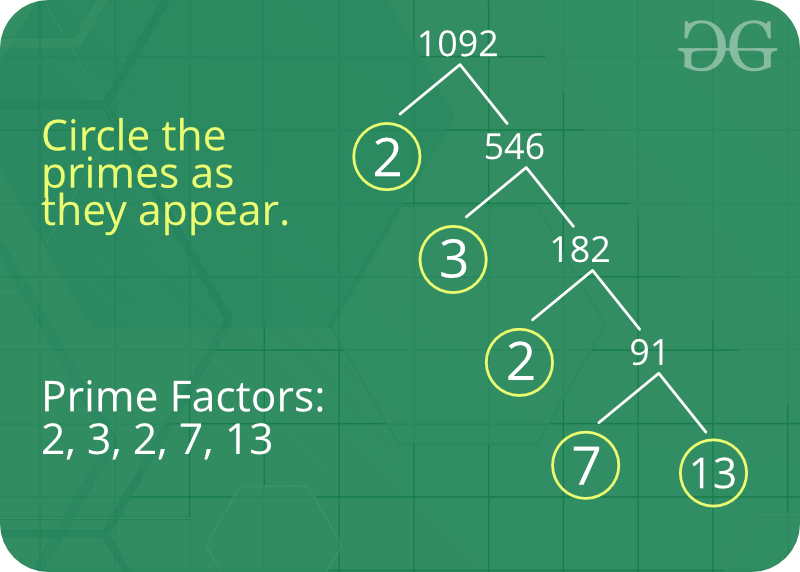
Algunos datos interesantes sobre Prime Factor: 

1. Solo hay un conjunto (¡único!) de factores primos para cualquier número.
2. Para mantener esta propiedad de factorizaciones primas únicas, es necesario que el número uno, 1, no se clasifique como ni primo ni compuesto.
3. Las factorizaciones primas pueden ayudarnos con la divisibilidad, la simplificación de fracciones y la búsqueda de denominadores comunes para las fracciones.
4. Pollard’s Rho es un algoritmo de descomposición en factores primos, particularmente rápido para un número compuesto grande con factores primos pequeños.
5. La criptografía es el estudio de los códigos secretos. La factorización prima es muy importante para las personas que intentan crear (o descifrar) códigos secretos basados ​​en números.

¿Cómo imprimir un factor primo de un número?
Solución ingenua: 
dado un número n, escriba una función para imprimir todos los factores primos de n. Por ejemplo, si el número de entrada es 12, la salida debería ser «2 2 3» y si el número de entrada es 315, la salida debería ser «3 3 5 7».

Los siguientes son los pasos para encontrar todos los factores primos: 

1. Mientras que n es divisible por 2, imprima 2 y divida n por 2.
2. Después del paso 1, n debe ser impar. Ahora inicia un bucle desde i = 3 hasta la raíz cuadrada de n . Mientras i divide n , imprima i y divida n entre i , incremente i en 2 y continúe.
3. Si n es un número primo y es mayor que 2, entonces n no se convertirá en 1 en los dos pasos anteriores. Entonces imprima n si es mayor que 2.

// Program to print all prime factors 
# include <stdio.h> 
# include <math.h> 
     
// A function to print all prime factors of a given number n 
void primeFactors(int n) 
{ 
    // Print the number of 2s that divide n 
    while (n%2 == 0) 
    { 
        printf("%d ", 2); 
        n = n/2; 
    } 
     
    // n must be odd at this point.  So we can skip  
    // one element (Note i = i +2) 
    for (int i = 3; i <= sqrt(n); i = i+2) 
    { 
        // While i divides n, print i and divide n 
        while (n%i == 0) 
        { 
            printf("%d ", i); 
            n = n/i; 
        } 
    } 
     
    // This condition is to handle the case when n  
    // is a prime number greater than 2 
    if (n > 2) 
        printf ("%d ", n); 
} 
     
/* Driver program to test above function */
int main() 
{ 
    int n = 315; 
    primeFactors(n); 
    return 0; 
}

// Program to print all prime factors
import java.io.*;
import java.lang.Math;
 
class GFG {
    // A function to print all prime factors
    // of a given number n
    public static void primeFactors(int n)
    {
        // Print the number of 2s that divide n
        while (n % 2 == 0) {
            System.out.print(2 + " ");
            n /= 2;
        }
 
        // n must be odd at this point.  So we can
        // skip one element (Note i = i +2)
        for (int i = 3; i <= Math.sqrt(n); i += 2) {
            // While i divides n, print i and divide n
            while (n % i == 0) {
                System.out.print(i + " ");
                n /= i;
            }
        }
 
        // This condition is to handle the case when
        // n is a prime number greater than 2
        if (n > 2)
            System.out.print(n);
    }
 
    public static void main(String[] args)
    {
        int n = 315;
        primeFactors(n);
    }
}

# Python program to print prime factors
 
import math
 
# A function to print all prime factors of
# a given number n
def primeFactors(n):
     
    # Print the number of two's that divide n
    while n % 2 == 0:
        print 2,
        n = n / 2
         
    # n must be odd at this point
    # so a skip of 2 ( i = i + 2) can be used
    for i in range(3, int(math.sqrt(n))+1, 2):
         
        # while i divides n, print i ad divide n
        while n % i == 0:
            print i,
            n = n / i
             
    # Condition if n is a prime
    # number greater than 2
    if n > 2:
        print n
         
# Driver Program to test above function
 
n = 315
primeFactors(n)
 
# This code is contributed by Harshit Agrawal

// C# Program to print all prime factors
using System;
 
namespace prime {
public class GFG {
 
    // A function to print all prime
    // factors of a given number n
    public static void primeFactors(int n)
    {
        // Print the number of 2s that divide n
        while (n % 2 == 0) {
            Console.Write(2 + " ");
            n /= 2;
        }
 
        // n must be odd at this point. So we can
        // skip one element (Note i = i +2)
        for (int i = 3; i <= Math.Sqrt(n); i += 2) {
            // While i divides n, print i and divide n
            while (n % i == 0) {
                Console.Write(i + " ");
                n /= i;
            }
        }
 
        // This condition is to handle the case when
        // n is a prime number greater than 2
        if (n > 2)
            Console.Write(n);
    }
 
    // Driver Code
    public static void Main()
    {
        int n = 315;
        primeFactors(n);
    }
}
}
 
// This code is contributed by Sam007

<?php
// PHP Efficient program to print all
// prime factors of a given number
 
// function to print all prime
// factors of a given number n
function primeFactors($n)
{
     
    // Print the number of
    // 2s that divide n
    while($n % 2 == 0)
    {
        echo 2, " ";
        $n = $n / 2;
    }
 
    // n must be odd at this
    // point. So we can skip
    // one element (Note i = i +2)
    for ($i = 3; $i <= sqrt($n);
                   $i = $i + 2)
    {
         
        // While i divides n,
        // print i and divide n
        while ($n % $i == 0)
        {
            echo $i, " ";
            $n = $n / $i;
        }
    }
 
    // This condition is to
    // handle the case when n
    // is a prime number greater
    // than 2
    if ($n > 2)
        echo $n, " ";
}
 
    // Driver Code
    $n = 315;
    primeFactors($n);
 
// This code is contributed by aj_36
?>

<script>
 
// Javascript program to print all prime factors
// A function to print all prime
// factors of a given number n
function primeFactors(n)
{
    // Print the number of 2s that divide n
    while (n % 2 == 0)
    {
        document.write(2 + " ");
        n = Math.floor(n/2);
    }
 
    // n must be odd at this point. So we can skip
    // one element (Note i = i +2)
    for (let i = 3; i <= Math.sqrt(n); i = i + 2)
    {
        // While i divides n, print i and divide n
        while (n % i == 0)
        {
            document.write(i + " ");
            n = Math.floor(n/i);
        }
    }
 
    // This condition is to handle the case when n
    // is a prime number greater than 2
    if (n > 2)
        document.write(n + " ");
}
 
/* Driver code */
  
    let n = 315;
    primeFactors(n);
 
 
// This is code is contributed by Mayank Tyagi
 
</script>

Producción: 

3 3 5 7

Complejidad del tiempo: O(sqrt(n))

Espacio auxiliar: O(1)
¿Cómo funciona esto? 

• Los pasos 1 y 2 se encargan de los números compuestos y el paso 3 se ocupa de los números primos. Para probar que el algoritmo completo funciona, necesitamos probar que los pasos 1 y 2 realmente se encargan de los números compuestos. 
  Está claro que el paso 1 se encarga de los números pares. Después del paso 1, todos los factores primos restantes deben ser impares (la diferencia de dos factores primos debe ser al menos 2), esto explica por qué i se incrementa en 2.
• Ahora, la parte principal es que el bucle se ejecuta hasta la raíz cuadrada de n . Para probar que esta optimización funciona, consideremos la siguiente propiedad de los números compuestos. 

Todo número compuesto tiene al menos un factor primo menor o igual a la raíz cuadrada de sí mismo.

• Esta propiedad se puede probar usando una declaración contraria. Sean a y b dos factores de n tales que a*b = n. Si ambos son mayores que √n, entonces ab > √n, * √n, lo que contradice la expresión “a * b = n”.
• En el paso 2 del algoritmo anterior, ejecutamos un bucle y hacemos lo siguiente: 
  • Encuentre el menor factor primo i (debe ser menor que √n, )
  • Elimine todas las ocurrencias i de n dividiendo repetidamente n por i.
  • Repita los pasos a y b para dividir n e i = i + 2. Los pasos a y b se repiten hasta que n se convierte en 1 o en un número primo.

Solución eficiente:  

• Factorización prima usando Sieve O (log n) para consultas múltiples

Programas para encontrar el factor primo de un número  

• Factores primos distintos del producto de array
• N-ésimo factor primo de un número dado
• Programa para imprimir factores de un numero en pares
• Número de factores primos distintos de los primeros n números naturales
• Producto de factores primos únicos de un número

Más problemas relacionados con Prime Factor  

• Cuenta números del rango cuyos factores primos son solo 2 y 3
• Factores primos comunes de dos números
• Mínimo factor primo de números hasta n
• El divisor primo más pequeño de un número
• Suma de factores de un número mediante factorización prima
• Números con suma de dígitos igual a la suma de dígitos de todos sus factores primos
• Número que tiene el número máximo de factores primos distintos en el rango M a N

¡Artículos recientes sobre Prime Factor!