La regla de la potencia es una regla de uso común en derivadas. La regla de la potencia básicamente establece que la derivada de una variable elevada a una potencia n es n veces la variable elevada a una potencia n-1. La fórmula matemática de la regla de la potencia se puede escribir como:
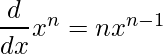
Dado que la diferenciación es una operación lineal en el espacio de funciones diferenciables, los polinomios también se pueden diferenciar usando esta regla. La regla de la potencia es la base de la serie de Taylor, ya que relaciona una serie de potencias con las derivadas de una función.
Ejemplos
Encuentra la derivada de
1.
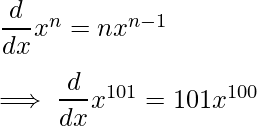
2.
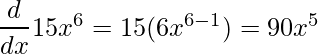
Regla de la potencia (reescribiendo la expresión)
De la ecuación y el ejemplo anteriores, ahora sabes cómo derivar una variable elevada a una potencia n. El punto a tener en cuenta es que n también puede ser fraccionario, por lo que la variable podría tener exponentes y estos exponentes son números reales. Para una mejor comprensión revisa los siguientes ejemplos:
Encuentre la derivada de
![Rendered by QuickLaTeX.com 1.\ \ x^{\dfrac{-3}{4}}\\\qquad\\ \dfrac{d}{dx}x^{\dfrac{-3}{4}}\ =\ \dfrac{-3}{4}x^{\dfrac{-3}{4}-1}\ =\ \dfrac{-3}{4}x^{\dfrac{-3-4}{4}}\ =\ \dfrac{-3}{4}x^{\dfrac{-7}{4}} \\\qquad\\\qquad\\ 2. \ \ \sqrt{x}\\\qquad\\ \dfrac{d}{dx}\sqrt{x}\ =\ \dfrac{d}{dx}x^{\dfrac{1}{2}}=\dfrac{1}{2}x^{\dfrac{1}{2}-1}\ =\ \dfrac{1}{2}x^{\dfrac{-1}{2}}\ =\ \dfrac{1}{2\sqrt{x}} \\\qquad\\\qquad\\ 3. \ \ \dfrac{1}{\sqrt[3]{x}}\\\qquad\\ \dfrac{d}{dx}\dfrac{1}{\sqrt[3]{x}}\ =\ \dfrac{d}{dx}x^{\dfrac{-1}{3}}\ =\ \dfrac{-1}{3}x^{\dfrac{-1}{3}-1}\ =\ \dfrac{-1}{3}x^{\dfrac{-1-3}{3}}\ =\ \dfrac{-1}{3}x^{\dfrac{-4}{3}}\ =\dfrac{-1}{3\sqrt[3]{x^{4}}} \\\qquad\\\qquad\\ 4. \ \ \sqrt[5]{x^7}\\\qquad\\ \dfrac{d}{dx}\sqrt[5]{x^7}\ =\ \dfrac{d}{dx}x^{\dfrac{7}{5}}\ =\ \dfrac{7}{5}x^{\dfrac{7-5}{5}}\ =\ \dfrac{7}{5}x^{\dfrac{2}{5}} \\\qquad\\\qquad\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-666aa279f5accd26679ae5ea04a959c0_l3.png)
Justificación de la regla de la potencia
Prueba:
Usando la definición de derivada podemos escribir
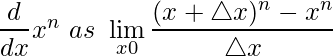
Usando el teorema del binomio desarrollamos (x + △x) n el término

Solo quedó el primer término, ya que no contiene un término △ x, por lo tanto,
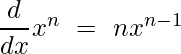
Publicación traducida automáticamente
Artículo escrito por somsagar2019 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA