Modelos lineales generalizados

Requisito previo:

El siguiente artículo analiza los modelos lineales generalizados (GLM) que explican cómo la regresión lineal y la regresión logística son miembros de una clase de modelos mucho más amplia. Los GLM se pueden usar para construir modelos para problemas de regresión y clasificación usando el tipo de distribución que mejor describa los datos o las etiquetas dadas para entrenar el modelo. A continuación se presentan algunos tipos de conjuntos de datos y las distribuciones correspondientes que nos ayudarían a construir el modelo para un tipo particular de datos (El término datos especificado aquí se refiere a los datos de salida o las etiquetas del conjunto de datos).

Datos de clasificación binaria: distribución de Bernoulli
Datos de valor real: distribución gaussiana
Datos de conteo: distribución de Poisson

Para comprender los GLM, comenzaremos definiendo familias exponenciales. Las familias exponenciales son una clase de distribuciones cuya función de densidad de probabilidad (PDF) se puede moldear de la siguiente forma:
$P(y;\eta) = b(y)exp(\eta^T * T(y) - a(\eta))\hspace{1mm}\\$

$\small \eta - Natural\hspace{1mm} parameter\hspace{1mm} (can\hspace{1mm} be\hspace{1mm} a \hspace{1mm}scalar \hspace{1mm}or\hspace{1mm} a \hspace{1mm}vector\hspace{1mm} quantity)\\ y - Label\hspace{1mm} for\hspace{1mm} data\\ T(y) - Sufficient\hspace{1mm} statistic\hspace{1mm} (Here, \hspace{1mm} it \hspace{1mm}will\hspace{1mm} be \hspace{1mm}equal \hspace{1mm}to \hspace{1mm}y)\\ a(\eta) - Log-partition \hspace{1mm}function (It \hspace{1mm}should \hspace{1mm}be \hspace{1mm}purely \hspace{1mm}a \hspace{1mm}function \hspace{1mm}of \hspace{1mm}eta)\\ b(y) - It \hspace{1mm}should\hspace{1mm} be \hspace{1mm}purely \hspace{1mm}a \hspace{1mm}function \hspace{1mm}of \hspace{1mm}y\\$

Prueba : la distribución de Bernoulli es un miembro de la familia exponencial.
$P(y;\phi) = \phi^y * (1-\phi)^{(1-y)}\\ \hspace{1cm}= exp(log(\phi^y * (1-\phi)^{(1-y)}))\\ \hspace{1cm}= exp(y * log(\phi) + (1-y) * log(1-\phi))\\ \hspace{1cm}= exp(y * log(\phi/1-\phi)) + log(1-\phi))\hspace{1mm}- Eq 2$
Por lo tanto, al comparar Eq1 y Eq2 :
$\eta = log(\phi/1-\phi)\\$
$\phi = 1/1+e^{-\eta} - Eq 3\\$
$b(y) = 1\\ T(y) = y\\ a(\eta) = -log(1-\phi)$

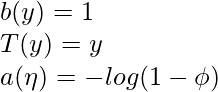
Nota: Como se mencionó anteriormente, el valor de phi (que es el mismo que la función de activación o sigmoide para la regresión logística) no es una coincidencia. Y se demostrará más adelante en el artículo cómo se puede derivar el modelo de regresión logística de la distribución de Bernoulli.

Prueba : la distribución gaussiana es un miembro de la familia exponencial.
$P(y, mu) = 1/\sqrt{2\pi} * exp(-1/2*(y-\mu)^2)\\ \hspace{1.5cm} = 1/\sqrt{2\pi}*exp(-1/2*y^{2}) * exp(\mu*y-1/2*\mu^{2}) - Eq3\\$
Por lo tanto, al comparar Eq1 y Eq3 :

$b(y) = 1/\sqrt{2\pi}*exp(-1/2*y^{2})\\ \eta = \mu\\ T(y) = y\\ a(\eta) = 1/2*\eta^2\\$

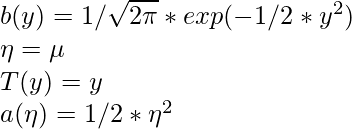
Construcción de GLM:
para construir GLM para un tipo particular de datos o, de manera más general, para problemas de clasificación lineal o logística, se deben considerar las siguientes tres suposiciones u opciones de diseño:
$y|x;\theta \sim exponential\hspace{1mm} family(\eta)\\ Given \hspace{1mm}x\hspace{1mm} our\hspace{1mm} goal\hspace{1mm} is\hspace{1mm} to\hspace{1mm} predict \hspace{1mm}T(y)\hspace{1mm} which \hspace{1mm}is \hspace{1mm}equal \hspace{1mm}to\hspace{1mm} y \hspace{1mm}in\hspace{1mm} our\hspace{1mm} case \hspace{1mm}or \hspace{1mm}h(x) = E[y|x] = \mu\\ \eta = \theta^T * x$
La primera suposición es que si x son los datos de entrada parametrizados por theta, la salida resultante o y será un miembro de la familia exponencial. Esto significa que si se nos proporcionan algunos datos etiquetados, nuestro objetivo es encontrar los parámetros theta correctos que se ajusten lo más posible al modelo dado. El tercer supuesto es el menos justificado y puede considerarse como una elección de diseño.

Modelo de Regresión Lineal:
Para mostrar que la Regresión Lineal es un caso especial de los GLM. Se considera que las etiquetas de salida son valores continuos y por tanto una distribución gaussiana . Entonces, tenemos
$y|x;\theta \sim \mathcal{N}(\mu, \sigma^2) \\ h_\theta(x) = E[y|x;\theta]\\ \hspace{0.9cm} = \mu\\ \hspace{0.9cm} = \eta\\ \hspace{0.9cm} = \theta^Tx$
La primera ecuación anterior corresponde a la primera suposición de que las etiquetas de salida (o variables objetivo ) deben ser miembros de una familia exponencial. La segunda ecuación corresponde a la suposición de que la hipótesis es igual al valor esperado o la media de la distribución . y por último, la tercera ecuación corresponde a la suposición de que el parámetro natural y los parámetros de entrada siguen una relación lineal.

Modelo de Regresión Logística:
Para mostrar que la Regresión Logística es un caso especial de los GLM. Se considera que las etiquetas de salida tienen valores binarios y, por lo tanto, son una distribución de Bernoulli . Entonces, tenemos
$y|x;\theta \sim Bernoulli(\phi) \\ h_\theta(x) = E[y|x;\theta]\\ \hspace{0.9cm} = \mu\\ \hspace{0.9cm} = 1/1+e^{-\eta}\\$
De la tercera suposición, se prueba que:
$\eta = \theta^Tx\\ h_\theta(x) = 1/1+e^{-\theta^Tx\\}$
La función que mapea el parámetro natural al parámetro canónico se conoce como la función de respuesta canónica (aquí, la función de partición logarítmica) y la inversa de la misma se conoce como la Función de enlace canónico .
Por lo tanto, al utilizar los tres supuestos mencionados anteriormente, se puede probar que la regresión logística y lineal pertenece a una familia mucho más grande de modelos conocidos como GLM.

Referencia:

Publicación traducida automáticamente

Artículo escrito por amanbhutani263 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta