Dadas dos arrays, la tarea de multiplicarlas. Las arrays pueden ser cuadradas o rectangulares.
Ejemplos:
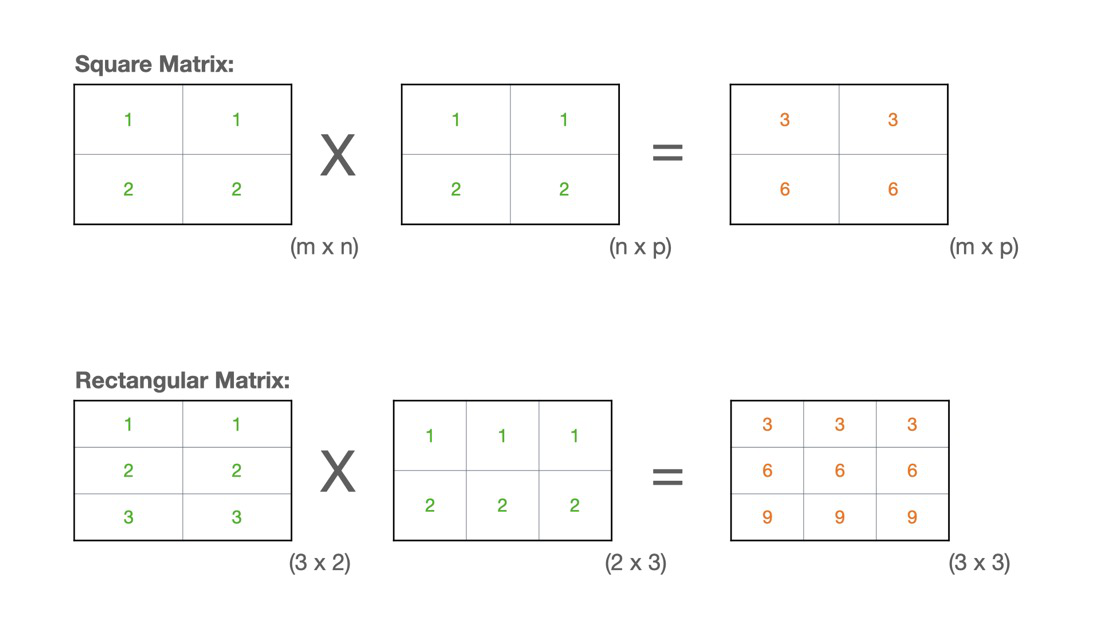
(Square Matrix Multiplication)
Input : mat1[m][n] = {
{1, 1},
{2, 2}
}
mat2[n][p] = {
{1, 1},
{2, 2}
}
Output : result[m][p] = {
{3, 3},
{6, 6}
}
(Rectangular Matrix Multiplication)
Input : mat1[3][2] = {
{1, 1},
{2, 2},
{3, 3}
}
mat2[2][3] = {
{1, 1, 1},
{2, 2, 2}
}
Output : result[3][3] = {
{3, 3, 3},
{6, 6, 6},
{9, 9, 9}
}
Multiplicación de dos Arrays Cuadradas o Rectangulares:
Este programa puede multiplicar dos arrays cuadradas o rectangulares cualesquiera.
El siguiente programa multiplica dos arrays cuadradas de tamaño 4 * 4.
También hay un ejemplo de array rectangular para el mismo código (comentado más abajo).
Podemos cambiar el valor de Matrix con el número de filas y columnas (de MACRO) para Matrix-1 y Matrix-2 para diferentes dimensiones.
Nota : i- El número de columnas en la Array-1 debe ser igual al número de filas en la Array-2.
ii- Salida de la multiplicación de Array-1 y Array-2, resultados con igual al número de filas de Array-1 y
el número de columnas de Matrix-2, es decir, rslt[R1][C2].
C
/*
* This C program can multiply any two square or rectangular matrices.
* The below program multiplies two square matrices of size 4 * 4.
* There is also an example of a rectangular matrix for the same code (commented below).
* We can change the Matrix value with the number of rows and columns (from MACROs) for Matrix-1
* and Matrix-2 for different dimensions.
*/
/*
* Note: i- The number of columns in Matrix-1 must be equal to the number of rows in Matrix-2.
* ii- Output of multiplication of Matrix-1 and Matrix-2, results with equal to the number
* of rows of Matrix-1 and the number of columns of Matrix-2 i.e. rslt[R1][C2].
*/
#include <stdio.h>
#include <stdlib.h>
// Edit MACROs here, according to your Matrix Dimensions for mat1[R1][C1] and mat2[R2][C2]
#define R1 4 // number of rows in Matrix-1
#define C1 4 // number of columns in Matrix-1
#define R2 4 // number of rows in Matrix-2
#define C2 4 // number of columns in Matrix-2
void mulMat(int mat1[][C1], int mat2[][C2]) {
int rslt[R1][C2];
printf("Multiplication of given two matrices is:\n\n");
for (int i = 0; i < R1; i++) {
for (int j = 0; j < C2; j++) {
rslt[i][j] = 0;
for (int k = 0; k < R2; k++) {
rslt[i][j] += mat1[i][k] * mat2[k][j];
}
printf("%d\t", rslt[i][j]);
}
printf("\n");
}
}
int main(void) {
// Square Matrices
// R1 = 4, C1 = 4 and R2 = 4, C2 = 4 (Update these values in MACROs)
int mat1[R1][C1] = {
{1, 1, 1, 1},
{2, 2, 2, 2},
{3, 3, 3, 3},
{4, 4, 4, 4}
};
int mat2[R2][C2] = {
{1, 1, 1, 1},
{2, 2, 2, 2},
{3, 3, 3, 3},
{4, 4, 4, 4}
};
/*
// Rectangular Matrices
// R1 = 3, C1 = 4 and R2 = 4, C2 = 3 (Update these values in MACROs)
int mat1[R1][C1] = {
{1, 1, 1, 1},
{2, 2, 2, 2},
{3, 3, 3, 3}
};
int mat2[R2][C2] = {
{1, 1, 1},
{2, 2, 2},
{3, 3, 3},
{4, 4, 4}
};
*/
if (C1 != R2) {
printf("The number of columns in Matrix-1 must be equal to the number of rows in "
"Matrix-2\n");
printf("Please update MACROs value according to your array dimension in "
"#define section\n");
exit(EXIT_FAILURE);
}
mulMat(mat1, mat2);
return 0;
}
// This code is contributed by Manish Kumar (mkumar2789)
C++
/*
* This C++ program can multiply any two square or rectangular matrices.
* The below program multiplies two square matrices of size 4 * 4.
* There is also an example of a rectangular matrix for the same code (commented below).
* We can change the Matrix value with the number of rows and columns (from MACROs) for Matrix-1
* and Matrix-2 for different dimensions.
*/
/*
* Note: i- The number of columns in Matrix-1 must be equal to the number of rows in Matrix-2.
* ii- Output of multiplication of Matrix-1 and Matrix-2, results with equal to the number
* of rows of Matrix-1 and the number of columns of Matrix-2 i.e. rslt[R1][C2].
*/
#include <iostream>
using namespace std;
// Edit MACROs here, according to your Matrix Dimensions for mat1[R1][C1] and mat2[R2][C2]
#define R1 4 // number of rows in Matrix-1
#define C1 4 // number of columns in Matrix-1
#define R2 4 // number of rows in Matrix-2
#define C2 4 // number of columns in Matrix-2
void mulMat(int mat1[][C1], int mat2[][C2]) {
int rslt[R1][C2];
cout << "Multiplication of given two matrices is:\n" << endl;
for (int i = 0; i < R1; i++) {
for (int j = 0; j < C2; j++) {
rslt[i][j] = 0;
for (int k = 0; k < R2; k++) {
rslt[i][j] += mat1[i][k] * mat2[k][j];
}
cout << rslt[i][j] << "\t";
}
cout << endl;
}
}
int main(void) {
// Square Matrices
// R1 = 4, C1 = 4 and R2 = 4, C2 = 4 (Update these values in MACROs)
int mat1[R1][C1] = {
{1, 1, 1, 1},
{2, 2, 2, 2},
{3, 3, 3, 3},
{4, 4, 4, 4}
};
int mat2[R2][C2] = {
{1, 1, 1, 1},
{2, 2, 2, 2},
{3, 3, 3, 3},
{4, 4, 4, 4}
};
/*
// Rectangular Matrices
// R1 = 3, C1 = 4 and R2 = 4, C2 = 3 (Update these values in MACROs)
int mat1[R1][C1] = {
{1, 1, 1, 1},
{2, 2, 2, 2},
{3, 3, 3, 3}
};
int mat2[R2][C2] = {
{1, 1, 1},
{2, 2, 2},
{3, 3, 3},
{4, 4, 4}
};
*/
if (C1 != R2) {
cout << "The number of columns in Matrix-1 must be equal to the number of rows in "
"Matrix-2" << endl;
cout << "Please update MACROs according to your array dimension in #define section"
<< endl;
exit(EXIT_FAILURE);
}
mulMat(mat1, mat2);
return 0;
}
// This code is contributed by Manish Kumar (mkumar2789)
Java
/*
* This Java program can multiply any two square or
* rectangular matrices. The below program multiplies two
* square matrices of size 4 * 4. There is also an example
* of a rectangular matrix for the same code (commented
* below). We can change the Matrix value with the number of
* rows and columns for Matrix-1 and Matrix-2
* for different dimensions.
*/
/*
* Note: i- The number of columns in Matrix-1 must be equal
* to the number of rows in Matrix-2. ii- Output of
* multiplication of Matrix-1 and Matrix-2, results with
* equal to the number of rows of Matrix-1 and the number of
* columns of Matrix-2 i.e. rslt[R1][C2].
*/
import java.io.*;
import java.util.*;
class GFG {
static int R1 = 4; // number of rows in Matrix-1
static int C1 = 4; // number of columns in Matrix-1
static int R2 = 4; // number of rows in Matrix-2
static int C2 = 4; // number of columns in Matrix-2
// This function multiplies mat1[][]
// and mat2[][], and stores the result
// in res[][]
static void mulMat(int[][] mat1, int[][] mat2)
{
// To store result
int[][] rslt = new int[R1][C2];
System.out.println("Multiplication of given two matrices is:");
int i, j, k;
for (i = 0; i < R1; i++) {
for (j = 0; j < C2; j++) {
rslt[i][j] = 0;
for (k = 0; k < R2; k++)
rslt[i][j] += mat1[i][k] * mat2[k][j];
System.out.print(rslt[i][j] + " ");
}
System.out.println("");
}
}
// Driver program
public static void main (String[] args) {
int[][] mat1 = { { 1, 1, 1, 1 },
{ 2, 2, 2, 2 },
{ 3, 3, 3, 3 },
{ 4, 4, 4, 4 } };
int[][] mat2 = { { 1, 1, 1, 1 },
{ 2, 2, 2, 2 },
{ 3, 3, 3, 3 },
{ 4, 4, 4, 4 } };
/*
// Rectangular Matrices
// R1 = 3, C1 = 4 and R2 = 4, C2 = 3 (Update these values in the global variables)
int mat1[][] = {
{1, 1, 1, 1},
{2, 2, 2, 2},
{3, 3, 3, 3} };
int mat2[][] = {
{1, 1, 1},
{2, 2, 2},
{3, 3, 3},
{4, 4, 4} };
*/
if (C1 != R2) {
System.out.println("The number of columns in Matrix-1 must be equal to the number of rows in Matrix-2");
System.out.println("Please update the global variables according to your array dimension");
}
else {
mulMat(mat1, mat2);
}
}
}
//This code is contributed by shruti456rawal
Python3
# 4x4 matrix multiplication using Python3
# Function definition
def mulMat(mat1, mat2, R1, R2, C1, C2):
# List to store matrix multiplication result
rslt = [[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]]
for i in range(0, R1):
for j in range(0, C2):
for k in range(0, R2):
rslt[i][j] += mat1[i][k] * mat2[k][j]
for i in range(0, R1):
for j in range(0, C2):
print(rslt[i][j], end=" ")
print("\n", end="")
R1 = 4
R2 = 4
C1 = 4
C2 = 4
# First matrix. M is a list
mat1 = [[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3],
[4, 4, 4, 4]]
# Second matrix. N is a list
mat2 = [[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3],
[4, 4, 4, 4]]
if C1 != R2:
print("The number of columns in Matrix-1 must be equal to the number of rows in " + "Matrix-2", end='')
print("\n", end='')
print("Please update MACROs according to your array dimension in #define section", end='')
print("\n", end='')
else:
# Call matrix_multiplication function
mulMat(mat1, mat2, R1, R2, C1, C2)
# This code is contributed by Aarti_Rathi
C#
/*
* This C# program can multiply any two square or
* rectangular matrices. The below program multiplies two
* square matrices of size 4 * 4. There is also an example
* of a rectangular matrix for the same code (commented
* below). We can change the Matrix value with the number of
* rows and columns (from MACROs) for Matrix-1 and Matrix-2
* for different dimensions.
*/
/*
* Note: i- The number of columns in Matrix-1 must be equal
* to the number of rows in Matrix-2. ii- Output of
* multiplication of Matrix-1 and Matrix-2, results with
* equal to the number of rows of Matrix-1 and the number of
* columns of Matrix-2 i.e. rslt[R1][C2].
*/
using System;
class GFG {
static int R1 = 4; // number of rows in Matrix-1
static int C1 = 4; // number of columns in Matrix-1
static int R2 = 4; // number of rows in Matrix-2
static int C2 = 4; // number of columns in Matrix-2
// This function multiplies mat1[][]
// and mat2[][], and stores the result
// in res[][]
static void mulMat(int[, ] mat1, int[, ] mat2)
{
// To store result
int[, ] rslt = new int[R1, C2];
Console.WriteLine(
"Multiplication of given two matrices is:");
int i, j, k;
for (i = 0; i < R1; i++) {
for (j = 0; j < C2; j++) {
rslt[i, j] = 0;
for (k = 0; k < R2; k++)
rslt[i, j] += mat1[i, k] * mat2[k, j];
Console.Write(rslt[i, j] + "\t");
}
Console.WriteLine();
}
}
// Driver code
public static void Main()
{
int[, ] mat1 = { { 1, 1, 1, 1 },
{ 2, 2, 2, 2 },
{ 3, 3, 3, 3 },
{ 4, 4, 4, 4 } };
int[, ] mat2 = { { 1, 1, 1, 1 },
{ 2, 2, 2, 2 },
{ 3, 3, 3, 3 },
{ 4, 4, 4, 4 } };
if (C1 != R2) {
Console.WriteLine(
"The number of columns in Matrix-1 must be equal to the number of rows in Matrix-2");
Console.WriteLine(
"Please update MACROs according to your array dimension in #define section");
}
else {
mulMat(mat1, mat2);
}
}
}
// This code is contributed by Aarti_Rathi
Javascript
var R1 = 4;
// number of rows in Matrix-1
var C1 = 4;
// number of columns in Matrix-1
var R2 = 4;
// number of rows in Matrix-2
var C2 = 4;
// number of columns in Matrix-2
// This function multiplies mat1[][]
// and mat2[][], and stores the result
// in res[][]
function mulMat(mat1, mat2)
{
// To store result
var rslt = Array(R1).fill(0).map(()=>new Array(C2).fill(0));
console.log("Multiplication of given two matrices is:");
var i = 0;
var j = 0;
var k = 0;
for (i = 0; i < R1; i++)
{
for (j = 0; j < C2; j++)
{
rslt[i][j] = 0;
for (k = 0; k < R2; k++)
{
rslt[i][j] += mat1[i][k] * mat2[k][j];
}
console.log(rslt[i][j] + " ");
}
console.log("");
}
}
// Driver program
var mat1 = [[1, 1, 1, 1], [2, 2, 2, 2], [3, 3, 3, 3], [4, 4, 4, 4]];
var mat2 = [[1, 1, 1, 1], [2, 2, 2, 2], [3, 3, 3, 3], [4, 4, 4, 4]];
// // Rectangular Matrices
// // R1 = 3, C1 = 4 and R2 = 4, C2 = 3 (Update these values in the global variables)
// int mat1[][] = {
// {1, 1, 1, 1},
// {2, 2, 2, 2},
// {3, 3, 3, 3} };
// int mat2[][] = {
// {1, 1, 1},
// {2, 2, 2},
// {3, 3, 3},
// {4, 4, 4} };
if (C1 != R2)
{
console.log("The number of columns in Matrix-1 must be equal to the number of rows in Matrix-2");
console.log("Please update the global variables according to your array dimension");
}
else
{
mulMat(mat1, mat2);
}
// This code is contributed by Aarti_Rathi
Multiplication of given two arrays is: 10 10 10 10 20 20 20 20 30 30 30 30 40 40 40 40
Multiplicación de Arrays Cuadradas:
El siguiente programa multiplica dos arrays cuadradas de tamaño 4*4, podemos cambiar N por diferentes dimensiones.
C++
// C++ program to multiply
// two square matrices.
#include <iostream>
using namespace std;
#define N 4
// This function multiplies
// mat1[][] and mat2[][], and
// stores the result in res[][]
void multiply(int mat1[][N],
int mat2[][N],
int res[][N])
{
int i, j, k;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
res[i][j] = 0;
for (k = 0; k < N; k++)
res[i][j] += mat1[i][k] * mat2[k][j];
}
}
}
// Driver Code
int main()
{
int i, j;
int res[N][N]; // To store result
int mat1[N][N] = { { 1, 1, 1, 1 },
{ 2, 2, 2, 2 },
{ 3, 3, 3, 3 },
{ 4, 4, 4, 4 } };
int mat2[N][N] = { { 1, 1, 1, 1 },
{ 2, 2, 2, 2 },
{ 3, 3, 3, 3 },
{ 4, 4, 4, 4 } };
multiply(mat1, mat2, res);
cout << "Result matrix is \n";
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++)
cout << res[i][j] << " ";
cout << "\n";
}
return 0;
}
// This code is contributed
// by Soumik Mondal
C
// C program to multiply two square matrices.
#include <stdio.h>
#define N 4
// This function multiplies mat1[][] and mat2[][],
// and stores the result in res[][]
void multiply(int mat1[][N], int mat2[][N], int res[][N])
{
int i, j, k;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
res[i][j] = 0;
for (k = 0; k < N; k++)
res[i][j] += mat1[i][k] * mat2[k][j];
}
}
}
int main()
{
int mat1[N][N] = { { 1, 1, 1, 1 },
{ 2, 2, 2, 2 },
{ 3, 3, 3, 3 },
{ 4, 4, 4, 4 } };
int mat2[N][N] = { { 1, 1, 1, 1 },
{ 2, 2, 2, 2 },
{ 3, 3, 3, 3 },
{ 4, 4, 4, 4 } };
int res[N][N]; // To store result
int i, j;
multiply(mat1, mat2, res);
printf("Result matrix is \n");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++)
printf("%d ", res[i][j]);
printf("\n");
}
return 0;
}
Java
// Java program to multiply two square
// matrices.
import java.io.*;
class GFG {
static int N = 4;
// This function multiplies mat1[][]
// and mat2[][], and stores the result
// in res[][]
static void multiply(int mat1[][],
int mat2[][], int res[][])
{
int i, j, k;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
res[i][j] = 0;
for (k = 0; k < N; k++)
res[i][j] += mat1[i][k]
* mat2[k][j];
}
}
}
// Driver code
public static void main(String[] args)
{
int mat1[][] = { { 1, 1, 1, 1 },
{ 2, 2, 2, 2 },
{ 3, 3, 3, 3 },
{ 4, 4, 4, 4 } };
int mat2[][] = { { 1, 1, 1, 1 },
{ 2, 2, 2, 2 },
{ 3, 3, 3, 3 },
{ 4, 4, 4, 4 } };
// To store result
int res[][] = new int[N][N];
int i, j;
multiply(mat1, mat2, res);
System.out.println("Result matrix"
+ " is ");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++)
System.out.print(res[i][j]
+ " ");
System.out.println();
}
}
}
// This code is contributed by anuj_67.
Python3
# 4x4 matrix multiplication using Python3
# Function definition
def matrix_multiplication(M, N):
# List to store matrix multiplication result
R = [[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]]
for i in range(0, 4):
for j in range(0, 4):
for k in range(0, 4):
R[i][j] += M[i][k] * N[k][j]
for i in range(0, 4):
for j in range(0, 4):
# if we use print(), by default cursor moves to next line each time,
# Now we can explicitly define ending character or sequence passing
# second parameter as end ="<character or string>"
# syntax: print(<variable or value to print>, end ="<ending with>")
# Here space (" ") is used to print a gap after printing
# each element of R
print(R[i][j], end =" ")
print("\n", end ="")
# First matrix. M is a list
M = [[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3],
[4, 4, 4, 4]]
# Second matrix. N is a list
N = [[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3],
[4, 4, 4, 4]]
# Call matrix_multiplication function
matrix_multiplication(M, N)
# This code is contributed by Santanu
C#
// C# program to multiply two square
// matrices.
using System;
class GFG {
static int N = 4;
// This function multiplies mat1[][]
// and mat2[][], and stores the result
// in res[][]
static void multiply(int[, ] mat1,
int[, ] mat2, int[, ] res)
{
int i, j, k;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
res[i, j] = 0;
for (k = 0; k < N; k++)
res[i, j] += mat1[i, k]
* mat2[k, j];
}
}
}
// Driver code
public static void Main()
{
int[, ] mat1 = { { 1, 1, 1, 1 },
{ 2, 2, 2, 2 },
{ 3, 3, 3, 3 },
{ 4, 4, 4, 4 } };
int[, ] mat2 = { { 1, 1, 1, 1 },
{ 2, 2, 2, 2 },
{ 3, 3, 3, 3 },
{ 4, 4, 4, 4 } };
// To store result
int[, ] res = new int[N, N];
int i, j;
multiply(mat1, mat2, res);
Console.WriteLine("Result matrix"
+ " is ");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++)
Console.Write(res[i, j]
+ " ");
Console.WriteLine();
}
}
}
// This code is contributed by anuj_67.
PHP
<?php
// PHP program to multiply two
// square matrices.
// This function multiplies mat1[][] and
// mat2[][], and stores the result in res[][]
function multiply(&$mat1, &$mat2, &$res)
{
$N = 4;
for ($i = 0; $i < $N; $i++)
{
for ($j = 0; $j < $N; $j++)
{
$res[$i][$j] = 0;
for ($k = 0; $k < $N; $k++)
$res[$i][$j] += $mat1[$i][$k] *
$mat2[$k][$j];
}
}
}
// Driver Code
$mat1 = array(array(1, 1, 1, 1),
array(2, 2, 2, 2),
array(3, 3, 3, 3),
array(4, 4, 4, 4));
$mat2 = array(array(1, 1, 1, 1),
array(2, 2, 2, 2),
array(3, 3, 3, 3),
array(4, 4, 4, 4));
multiply($mat1, $mat2, $res);
$N = 4;
echo ("Result matrix is \n");
for ($i = 0; $i < $N; $i++)
{
for ($j = 0; $j < $N; $j++)
{
echo ($res[$i][$j]);
echo(" ");
}
echo ("\n");
}
// This code is contributed
// by Shivi_Aggarwal
?>
Javascript
<script>
// Javascript program to multiply
// two square matrices.
const N = 4;
// This function multiplies
// mat1[][] and mat2[][], and
// stores the result in res[][]
function multiply(mat1, mat2, res)
{
let i, j, k;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
res[i][j] = 0;
for (k = 0; k < N; k++)
res[i][j] += mat1[i][k] * mat2[k][j];
}
}
}
// Driver Code
let i, j;
// To store result
let res = new Array(N);
for (let k = 0; k < N; k++)
res[k] = new Array(N);
let mat1 = [ [ 1, 1, 1, 1 ],
[ 2, 2, 2, 2 ],
[ 3, 3, 3, 3 ],
[ 4, 4, 4, 4 ] ];
let mat2 = [ [ 1, 1, 1, 1 ],
[ 2, 2, 2, 2 ],
[ 3, 3, 3, 3 ],
[ 4, 4, 4, 4 ] ];
multiply(mat1, mat2, res);
document.write("Result matrix is <br>");
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++)
document.write(res[i][j] + " ");
document.write("<br>");
}
</script>
Result matrix is 10 10 10 10 20 20 20 20 30 30 30 30 40 40 40 40
Complejidad temporal: O(n 3 ). Se puede optimizar utilizando la multiplicación de arrays de Strassen
Espacio Auxiliar: O(n 2 )
Multiplicación de Arrays Rectangulares:
Usamos punteros en C para multiplicar a arrays. Consulte la siguiente publicación como requisito previo del código.
¿Cómo pasar una array 2D como parámetro en C?
C++
// C++ program to multiply two
// rectangular matrices
#include <bits/stdc++.h>
using namespace std;
// Multiplies two matrices mat1[][]
// and mat2[][] and prints result.
// (m1) x (m2) and (n1) x (n2) are
// dimensions of given matrices.
void multiply(int m1, int m2, int mat1[][2], int n1, int n2,
int mat2[][2])
{
int x, i, j;
int res[m1][n2];
for (i = 0; i < m1; i++)
{
for (j = 0; j < n2; j++)
{
res[i][j] = 0;
for (x = 0; x < m2; x++)
{
*(*(res + i) + j) += *(*(mat1 + i) + x)
* *(*(mat2 + x) + j);
}
}
}
for (i = 0; i < m1; i++)
{
for (j = 0; j < n2; j++)
{
cout << *(*(res + i) + j) << " ";
}
cout << "\n";
}
}
// Driver code
int main()
{
int mat1[][2] = { { 2, 4 }, { 3, 4 } };
int mat2[][2] = { { 1, 2 }, { 1, 3 } };
int m1 = 2, m2 = 2, n1 = 2, n2 = 2;
// Function call
multiply(m1, m2, mat1, n1, n2, mat2);
return 0;
}
// This code is contributed
// by Akanksha Rai(Abby_akku)
C
// C program to multiply two rectangular matrices
#include <stdio.h>
// Multiplies two matrices mat1[][] and mat2[][]
// and prints result.
// (m1) x (m2) and (n1) x (n2) are dimensions
// of given matrices.
void multiply(int m1, int m2, int mat1[][m2], int n1,
int n2, int mat2[][n2])
{
int x, i, j;
int res[m1][n2];
for (i = 0; i < m1; i++)
{
for (j = 0; j < n2; j++)
{
res[i][j] = 0;
for (x = 0; x < m2; x++)
{
*(*(res + i) + j) += *(*(mat1 + i) + x)
* *(*(mat2 + x) + j);
}
}
}
for (i = 0; i < m1; i++)
{
for (j = 0; j < n2; j++)
{
printf("%d ", *(*(res + i) + j));
}
printf("\n");
}
}
// Driver code
int main()
{
int mat1[][2] = { { 2, 4 }, { 3, 4 } };
int mat2[][2] = { { 1, 2 }, { 1, 3 } };
int m1 = 2, m2 = 2, n1 = 2, n2 = 2;
// Function call
multiply(m1, m2, mat1, n1, n2, mat2);
return 0;
}
Java
// Java program to multiply two matrices.
public class GFG
{
/**
* to find out matrix multiplication
*
* @param matrix1 First matrix
* @param rows1 Number of rows in matrix 1
* @param cols1 Number of columns in matrix 1
* @param matrix2 Second matrix
* @param rows2 Number of rows in matrix 2
* @param cols2 Number of columns in matrix 2
* @return the result matrix (matrix 1 and matrix 2
* multiplication)
*/
public static int[][] matrixMultiplication(
int[][] matrix1, int rows1, int cols1,
int[][] matrix2, int rows2, int cols2)
throws Exception
{
// Required condition for matrix multiplication
if (cols1 != rows2) {
throw new Exception("Invalid matrix given.");
}
// create a result matrix
int resultMatrix[][] = new int[rows1][cols2];
// Core logic for 2 matrices multiplication
for (int i = 0; i < resultMatrix.length; i++)
{
for (int j = 0;
j < resultMatrix[i].length;
j++)
{
for (int k = 0; k < cols1; k++)
{
resultMatrix[i][j]
+= matrix1[i][k] * matrix2[k][j];
}
}
}
return resultMatrix;
}
// Driver code
public static void main(String[] args) throws Exception
{
// Initial matrix 1 and matrix 2
int matrix1[][] = { { 2, 4 }, { 3, 4 } };
int matrix2[][] = { { 1, 2 }, { 1, 3 } };
// Function call to get a matrix multiplication
int resultMatrix[][] = matrixMultiplication(
matrix1, 2, 2, matrix2, 2, 2);
// Display result matrix
System.out.println("Result Matrix is:");
for (int i = 0; i < resultMatrix.length; i++)
{
for (int j = 0;
j < resultMatrix[i].length;
j++)
{
System.out.print(resultMatrix[i][j] + "\t");
}
System.out.println();
}
}
// This code is contributed by darshatandel1998 (Darshan
// Tandel)
}
Python3
# Python3 program to multiply two # rectangular matrices # Multiplies two matrices mat1[][] # and mat2[][] and prints result. # (m1) x (m2) and (n1) x (n2) are # dimensions of given matrices. def multiply(m1, m2, mat1, n1, n2, mat2): res = [[0 for x in range(n2)] for y in range (m1)] for i in range(m1): for j in range(n2): res[i][j] = 0 for x in range(m2): res[i][j] += (mat1[ i][x] * mat2[ x][j]) for i in range(m1): for j in range(n2): print (res[i][j], end = " ") print () # Driver code if __name__ == "__main__": mat1 = [[2, 4], [3, 4]] mat2 = [[1, 2], [1, 3]] m1, m2, n1, n2 = 2, 2, 2, 2 # Function call multiply(m1, m2, mat1, n1, n2, mat2) # This code is contributed by Chitranayal
C#
// C# program to multiply two
// rectangular matrices
using System;
class GFG{
// Multiplies two matrices mat1[][]
// and mat2[][] and prints result.
// (m1) x (m2) and (n1) x (n2) are
// dimensions of given matrices.
static void multiply(int m1, int m2, int[,] mat1,
int n1, int n2, int[,] mat2)
{
int x, i, j;
int[,] res = new int[m1, n2];
for(i = 0; i < m1; i++)
{
for(j = 0; j < n2; j++)
{
res[i, j] = 0;
for(x = 0; x < m2; x++)
{
res[i, j] += (mat1[i, x] *
mat2[x, j]);
}
}
}
for(i = 0; i < m1; i++)
{
for(j = 0; j < n2; j++)
{
Console.Write(res[i, j] + " ");
}
Console.WriteLine();
}
}
// Driver Code
static void Main()
{
int[,] mat1 = { { 2, 4 }, { 3, 4 } };
int[,] mat2 = { { 1, 2 }, { 1, 3 } };
int m1 = 2, m2 = 2, n1 = 2, n2 = 2;
// Function call
multiply(m1, m2, mat1, n1, n2, mat2);
}
}
// This code is contributed by divyeshrabadiya07
PHP
<?php
// PHP program to multiply two
// rectangular matrices
// Multiplies two matrices mat1[][]
// and mat2[][] and prints result.
// (m1) x (m2) and (n1) x (n2) are
// dimensions of given matrices.
function multiply($m1, $m2, $mat1,
$n1, $n2, $mat2)
{
for ($i = 0; $i < $m1; $i++)
{
for ($j = 0; $j < $n2; $j++)
{
$res[$i][$j] = 0;
for ($x = 0; $x < $m2; $x++)
{
$res[$i][$j] += $mat1[$i][$x] *
$mat2[$x][$j];
}
}
}
for ($i = 0; $i < $m1; $i++)
{
for ($j = 0; $j < $n2; $j++)
{
echo $res[$i][$j] . " ";
}
echo "\n";
}
}
// Driver code
$mat1 = array( array( 2, 4 ), array( 3, 4 ));
$mat2 = array( array( 1, 2 ), array( 1, 3 ));
$m1 = 2;
$m2 = 2;
$n1 = 2;
$n2 = 2;
//Function call
multiply($m1, $m2, $mat1, $n1, $n2, $mat2);
// This code is contributed by rathbhupendra
?>
Javascript
<script>
// Javascript program to multiply two
// rectangular matrices
// Multiplies two matrices mat1[][]
// and mat2[][] and prints result.
// (m1) x (m2) and (n1) x (n2) are
// dimensions of given matrices.
function multiply(m1, m2, mat1, n1, n2, mat2)
{
let x, i, j;
let res = new Array(m1);
for (i = 0; i < m1; i++)
res[i] = new Array(n2);
for (i = 0; i < m1; i++)
{
for (j = 0; j < n2; j++)
{
res[i][j] = 0;
for (x = 0; x < m2; x++)
{
res[i][j] += mat1[i][x] * mat2[x][j];
}
}
}
for (i = 0; i < m1; i++)
{
for (j = 0; j < n2; j++)
{
document.write(res[i][j] + " ");
}
document.write("<br>");
}
}
// Driver code
let mat1 = [ [ 2, 4 ], [ 3, 4 ] ];
let mat2 = [ [ 1, 2 ], [ 1, 3 ] ];
let m1 = 2, m2 = 2, n1 = 2, n2 = 2;
// Function call
multiply(m1, m2, mat1, n1, n2, mat2);
</script>
6 16 7 18
Complejidad temporal: O(n 3 ). Se puede optimizar utilizando la multiplicación de arrays de Strassen
Espacio Auxiliar: O(m1 * n2)
Este artículo es una contribución de Aditya Ranjan . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA