Dado un número m, encuentra todos los números que tienen m dígitos y son divisores de su rotación a la derecha. La rotación a la derecha de un número N es el resultado de rotar los dígitos de N un lugar a la derecha y envolver el dígito menos significativo para que se convierta en el dígito más significativo. Por ejemplo, la rotación a la derecha de 4356 es 6435.
Ejemplos:
Input: 2 Output: 11 22 33 44 55 66 77 88 99 Input: 6 Output: 102564 111111 128205 142857 153846 179487 205128 222222 230769 333333 444444 555555 666666 777777 888888 999999 128205 satisfies the condition as 128205 * 4 = 512820.
Enfoque de fuerza bruta :
El enfoque más simple es recorrer todos los números que son mayores o iguales a 10 m-1 y menores a 10 m y verificar si cumplen la condición requerida. Podemos comprobarlo en tiempo constante, por lo que la complejidad temporal de todo el proceso es O(10 m ), lo cual es factible solo para valores pequeños de m.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to Generating numbers that
// are divisor of their right-rotations
#include <bits/stdc++.h>
using namespace std;
// Function to check if N is a
// divisor of its right-rotation
bool rightRotationDivisor(int N)
{
int lastDigit = N % 10;
int rightRotation = (lastDigit * pow(10 ,int(log10(N))))
+ floor(N / 10);
return (rightRotation % N == 0);
}
// Function to generate m-digit
// numbers which are divisor of
// their right-rotation
void generateNumbers(int m)
{
for (int i=pow(10,(m - 1));i<pow(10 , m);i++)
if (rightRotationDivisor(i))
cout<<i<<endl;
}
// Driver code
int main()
{
int m = 3;
generateNumbers(m);
}
Java
// Java program to Generating numbers that
// are divisor of their right-rotations
public class GFG {
// Function to check if N is a
// divisor of its right-rotation
static boolean rightRotationDivisor(int N)
{
int lastDigit = N % 10;
int rightRotation = (int)(lastDigit * Math.pow(10 ,(int)(Math.log10(N)))
+ Math.floor(N / 10));
return (rightRotation % N == 0);
}
// Function to generate m-digit
// numbers which are divisor of
// their right-rotation
static void generateNumbers(int m)
{
for (int i= (int)Math.pow(10,(m - 1)); i < Math.pow(10 , m);i++)
if (rightRotationDivisor(i))
System.out.println(i);
}
// Driver code
public static void main(String args[])
{
int m = 3;
generateNumbers(m);
}
// This Code is contributed by ANKITRAI1
}
Python3
# Python program to Generating numbers that are # divisor of their right-rotations from math import log10 # Function to check if N is a # divisor of its right-rotation def rightRotationDivisor(N): lastDigit = N % 10 rightRotation = (lastDigit * 10 ** int(log10(N)) + N // 10) return rightRotation % N == 0 # Function to generate m-digit # numbers which are divisor of # their right-rotation def generateNumbers(m): for i in range(10 ** (m - 1), 10 ** m): if rightRotationDivisor(i): print(i) # Driver code m = 3 generateNumbers(m)
C#
// C# program to Generating numbers that
// are divisor of their right-rotations
using System;
public class GFG{
// Function to check if N is a
// divisor of its right-rotation
static bool rightRotationDivisor(int N)
{
int lastDigit = N % 10;
int rightRotation = (int)(lastDigit * Math.Pow(10 ,(int)(Math.Log10(N)))
+ Math.Floor((double)N/10));
return (rightRotation % N == 0);
}
// Function to generate m-digit
// numbers which are divisor of
// their right-rotation
static void generateNumbers(int m)
{
for (int i= (int)Math.Pow(10,(m - 1)); i < Math.Pow(10 , m);i++)
if (rightRotationDivisor(i))
Console.WriteLine(i);
}
// Driver code
public static void Main()
{
int m = 3;
generateNumbers(m);
}
}
// This code is contributed by 29AjayKumar
PHP
<?php
// PHP program to Generating numbers that
// are divisor of their right-rotations
// Function to check if N is a
// divisor of its right-rotation
function rightRotationDivisor($N)
{
$lastDigit = $N % 10;
$rightRotation = ($lastDigit * pow(10 ,
(int)(log10($N)))) +
floor($N / 10);
return ($rightRotation % $N == 0);
}
// Function to generate m-digit
// numbers which are divisor of
// their right-rotation
function generateNumbers($m)
{
for ($i = pow(10, ($m - 1));
$i < pow(10 , $m); $i++)
if (rightRotationDivisor($i))
echo $i . "\n";
}
// Driver code
$m = 3;
generateNumbers($m);
// This code is contributed
// by ChitraNayal
?>
Javascript
<script>
// Javascript program to Generating numbers that
// are divisor of their right-rotations
// Function to check if N is a
// divisor of its right-rotation
function rightRotationDivisor(N)
{
let lastDigit = N % 10;
let rightRotation = (lastDigit * Math.pow(10 ,
Math.floor((Math.log10(N)))) + Math.floor(N / 10));
return (rightRotation % N == 0);
}
// Function to generate m-digit
// numbers which are divisor of
// their right-rotation
function generateNumbers(m)
{
for (let i= Math.floor(Math.pow(10,(m - 1))); i <
Math.floor(Math.pow(10 , m));i++)
if (rightRotationDivisor(i))
document.write(i+"<br>");
}
// Driver code
let m = 3;
generateNumbers(m);
// This code is contributed by avanitrachhadiya2155
</script>
111 222 333 444 555 666 777 888 999
Complejidad de tiempo : O (10 m )
Enfoque eficiente :
Sea d m d m-1 ..d 3 d 2 d 1 la forma general de los números que queremos generar. Tome x = re metro re m -1 ..d 3 re 2 y y = re 1 . La condición que queremos satisfacer es y * 10 m – 1 + x = k * (10x + y) donde k es un número entero positivo. Reorganizando los términos, obtenemos x = (y * (10 m-1 – k)) / (10k – 1) . Por lo tanto, si fijamos el valor de y y k, podemos obtener un valor de x tal que 10x + y es un número que necesitamos generar.
El valor de y puede variar de 1 a 9; observe que no tendremos el caso y = 0 ya que eso haría que la rotación correcta y * 10 m – 1 + x tenga m – 1 dígito, y la condición requerida nunca se cumplirá.
Requerimos que x tenga exactamente m – 1 dígito, es decir
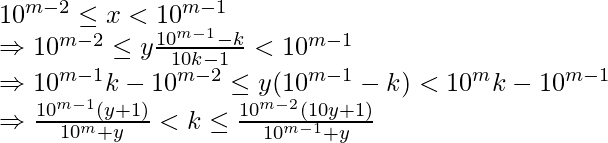
We can observe that the lower bound is always less than unity, so we can keep it at 1 since k has to be a positive integer.
We can use these results to obtain a highly efficient solution that runs with constant time complexity, i.e. O(1). An important point to note is that the numbers obtained may not be in a sorted form, so we need to store and explicitly sort them if we wish to obtain the numbers in a sorted fashion.
Below is the implementation of the above approach:
C++
// C++ program to Generating
// numbers that are divisor
// of their right-rotations
#include <bits/stdc++.h>
using namespace std;
// Function to generate m-digit
// numbers which are divisor of
// their right-rotation
void generateNumbers(int m)
{
vector<int> numbers;
int k_max, x;
for (int y = 0; y < 10; y++)
{
k_max = (int)(pow(10, m - 2) *
(10 * y + 1)) /
(int)(pow(10, m - 1) + y);
for (int k = 1; k <= k_max; k++)
{
x = (int)(y * (pow(10, m - 1) - k)) /
(10 * k - 1);
if ((int)(y * (pow(10, m - 1) - k)) %
(10 * k - 1) == 0)
numbers.push_back(10 * x + y);
}
}
sort(numbers.begin(), numbers.end());
for (int i = 0; i < numbers.size(); i++)
cout << (numbers[i]) << endl;
}
// Driver code
int main()
{
int m = 3;
generateNumbers(m);
}
// This code is contributed by Chitranayal
Java
// Java program to Generating numbers that
// are divisor of their right-rotations
import java.util.*;
import java.io.*;
class GFG
{
// Function to generate m-digit
// numbers which are divisor of
// their right-rotation
static void generateNumbers(int m)
{
ArrayList<Integer> numbers = new ArrayList<>();
int k_max, x;
for (int y = 0; y < 10; y++)
{
k_max = (int)(Math.pow(10,m-2) * (10 * y + 1)) /
(int)(Math.pow(10, m-1) + y);
for (int k = 1; k <= k_max; k++)
{
x = (int)(y*(Math.pow(10,m-1)-k)) / (10 * k -1);
if ((int)(y*(Math.pow(10,m-1)-k)) % (10 * k -1) == 0)
numbers.add(10 * x + y);
}
}
Collections.sort(numbers);
for (int i = 0; i < numbers.size(); i++)
System.out.println(numbers.get(i));
}
// Driver code
public static void main(String args[])
{
int m = 3;
generateNumbers(m);
}
}
// This code is contributed by rachana soma
Python 3
# Python program to Generating numbers that # are divisor of their right-rotations from math import log10 # Function to generate m-digit # numbers which are divisor of # their right-rotation def generateNumbers(m): numbers = [] for y in range(1, 10): k_max = ((10 ** (m - 2) * (10 * y + 1)) // (10 ** (m - 1) + y)) for k in range(1, k_max + 1): x = ((y * (10 ** (m - 1) - k)) // (10 * k - 1)) if ((y * (10 ** (m - 1) - k)) % (10 * k - 1) == 0): numbers.append(10 * x + y) for n in sorted(numbers): print(n) # Driver code m = 3 generateNumbers(m)
C#
// C# program to Generating numbers that
// are divisor of their right-rotations
using System;
using System.Collections.Generic;
class GFG
{
// Function to generate m-digit
// numbers which are divisor of
// their right-rotation
static void generateNumbers(int m)
{
List<int> numbers = new List<int>();
int k_max, x;
for (int y = 0; y < 10; y++)
{
k_max = (int)(Math.Pow(10, m - 2) * (10 * y + 1)) /
(int)(Math.Pow(10, m - 1) + y);
for (int k = 1; k <= k_max; k++)
{
x = (int)(y * (Math.Pow(10, m - 1) - k)) /
(10 * k - 1);
if ((int)(y * (Math.Pow(10, m - 1) - k)) %
(10 * k - 1) == 0)
numbers.Add(10 * x + y);
}
}
numbers.Sort();
for (int i = 0; i < numbers.Count; i++)
Console.WriteLine(numbers[i]);
}
// Driver code
public static void Main(String []args)
{
int m = 3;
generateNumbers(m);
}
}
// This code is contributed by PrinciRaj1992
Javascript
<script>
// Javascript program to Generating numbers that
// are divisor of their right-rotations
// Function to generate m-digit
// numbers which are divisor of
// their right-rotation
function generateNumbers(m)
{
let numbers = [];
let k_max, x;
for (let y = 0; y < 10; y++)
{
k_max = Math.floor((Math.pow(10,m-2) * (10 * y + 1)) /
Math.floor(Math.pow(10, m-1) + y));
for (let k = 1; k <= k_max; k++)
{
x = Math.floor((y*(Math.pow(10,m-1)-k)) / (10 * k -1));
if (Math.floor((y*(Math.pow(10,m-1)-k)) % (10 * k -1)) == 0)
numbers.push(10 * x + y);
}
}
numbers.sort(function(a,b){return a-b;});
for (let i = 0; i < numbers.length; i++)
document.write(numbers[i]+"<br>");
}
// Driver code
let m = 3;
generateNumbers(m);
// This code is contributed by rag2127
</script>
111 222 333 444 555 666 777 888 999
Complejidad del tiempo : O(1)
Espacio Auxiliar: O(n)
Publicación traducida automáticamente
Artículo escrito por vaibhav29498 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA