Probabilidades de registro

Odds (probabilidades de éxito): Se define como las posibilidades de éxito divididas por las posibilidades de fracaso. Digamos que hay un 90 % de posibilidades de que ganar una apuesta implique que las «probabilidades están a nuestro favor», ya que las probabilidades de ganar son del 90 % mientras que las probabilidades de perder son solo del 10 %. También se conoce como razón de probabilidades, ya que tiene la forma de una razón. Entonces, la razón impar del ejemplo discutido anteriormente sería:

Formalmente, la razón de posibilidades de un evento A se define como la probabilidad de que A ocurra sobre la probabilidad de que A no ocurra (es decir, complemento de A). (Como se muestra en la ecuación dada a continuación)

Odds, no es lo mismo que probabilidad

Es importante tener en cuenta que las probabilidades de que ocurra un evento no son las mismas que su probabilidad. Digamos que las probabilidades de que mi equipo de baloncesto gane el torneo son de 1 a 5. 

Las probabilidades de que mi equipo gane =   pero,
La probabilidad de que mi equipo gane = 

Sin embargo, matemáticamente, el resultado final sigue siendo el mismo para ambos, ya que en el caso de la probabilidad, el denominador se cancela. (Como se muestra abajo)

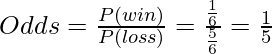
problema con las probabilidades

El problema con la relación de probabilidades se debe a la presencia de asimetría creada entre las probabilidades de ganar y las probabilidades de perder. Tratemos de entender esto con la ayuda de un ejemplo. 72 países participan en los Juegos de la Commonwealth. 

Teniendo en cuenta que todos los países tienen las mismas posibilidades de ganar, las probabilidades de que el equipo indio gane el oro son en contra, 1 a 71 o 
Pero suponiendo un escenario ideal donde las probabilidades de que el equipo indio gane el oro son a favor, 71 a 1 o 

Como se observa en la figura 1, cuando las probabilidades están en contra nuestra, el valor siempre tiende a estar entre 0 y 1, que es un valor muy pequeño. Sin embargo, si las probabilidades están a nuestro favor, el valor puede estar entre 1 e infinito, ¡lo que puede ser un valor muy grande! Para resolver este problema, apareció el concepto de probabilidades logarítmicas.

Logaritmo de probabilidades : Es el logaritmo de la razón de probabilidades. (Como se muestra en la ecuación dada a continuación)

Según el ejemplo mencionado anteriormente, 

El registro de probabilidades de que el equipo indio gane un oro es en contra, 1 a 71 = 

El registro de probabilidades de que el equipo indio gane el oro está a favor, 71 a 1 = 

Como se observa en la Fig. 2, tomar el logaritmo de la razón de posibilidades genera cierta simetría en los resultados, lo que facilita su interpretación y uso en diversas estadísticas. 

NOTA INTERESANTE: ¡ Las probabilidades logarítmicas de un determinado evento dan una distribución normal cuando se trazan en un histograma! Esto es lo que hace que las probabilidades logarítmicas sean tan útiles. 

ejemplo de la vida real 

Las probabilidades de registro se utilizan en la investigación médica para predecir la probabilidad de síntomas que el sujeto puede tener en función de sus síntomas anteriores. Considere el siguiente ejemplo. Se realiza una investigación médica en 1000 sujetos de prueba que muestran síntomas de fiebre y tos/resfriado al azar. El objetivo es averiguar la probabilidad de que las personas que tienen tos/resfriado tengan muchas más posibilidades de tener fiebre o no. (Datos proporcionados a continuación en la Fig. 3.)

Solución: 

Las probabilidades de que una persona con tos/resfriado también tenga fiebre 

Las probabilidades de que una persona que no tiene tos/resfriado, también tenga fiebre 

∴ Las cuotas objetivas 

y  , dotar de simetría a los diversos resultados que se pueden obtener de la investigación. 

Esto muestra que la probabilidad de que una persona con tos/resfriado también tenga fiebre es 21 veces mayor que la probabilidad de que una persona no tenga tos/resfriado. El logaritmo de las probabilidades o razón de probabilidades es muy similar a la prueba R-cuadrado, ya que indica la relación entre dos factores. Por lo tanto, se puede decir que cuanto mayor sea el valor de las cuotas, más relacionados tienden a estar los dos factores. Este es el poder del logaritmo de probabilidades/razón de probabilidades.