Dado un valor de ángulo, debe calcular los valores de Sin y Cos correspondientes a él.
Para la función sen
Ejemplos:
Input : 90 Output : 1
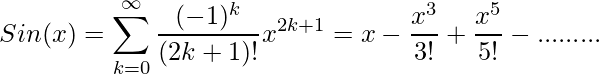
C++
// CPP code for implementing sin function
#include <iostream>
#include <math.h>
using namespace std;
// Function for calculating sin value
void cal_sin(float n)
{
float accuracy = 0.0001, denominator, sinx, sinval;
// Converting degrees to radian
n = n * (3.142 / 180.0);
float x1 = n;
// maps the sum along the series
sinx = n;
// holds the actual value of sin(n)
sinval = sin(n);
int i = 1;
do
{
denominator = 2 * i * (2 * i + 1);
x1 = -x1 * n * n / denominator;
sinx = sinx + x1;
i = i + 1;
} while (accuracy <= fabs(sinval - sinx));
cout << sinx;
}
// Main function
int main()
{
float n = 90;
cal_sin(n);
return 0;
}
Java
import static java.lang.Math.sin;
// JAVA code for implementing sin function
class GFG {
// Function for calculating sin value
static void cal_sin(float n)
{
float accuracy = (float) 0.0001, denominator, sinx, sinval;
// Converting degrees to radian
n = n * (float)(3.142 / 180.0);
float x1 = n;
// maps the sum along the series
sinx = n;
// holds the actual value of sin(n)
sinval = (float)sin(n);
int i = 1;
do
{
denominator = 2 * i * (2 * i + 1);
x1 = -x1 * n * n / denominator;
sinx = sinx + x1;
i = i + 1;
} while (accuracy <= sinval - sinx);
System.out.println(sinx);
}
// Main function
public static void main(String[] args) {
float n = 90;
cal_sin(n);
}
}
Python3
# Python3 code for implementing # sin function import math; # Function for calculating sin value def cal_sin(n): accuracy = 0.0001; # Converting degrees to radian n = n * (3.142 / 180.0); x1 = n; # maps the sum along the series sinx = n; # holds the actual value of sin(n) sinval = math.sin(n); i = 1; while(True): denominator = 2 * i * (2 * i + 1); x1 = -x1 * n * n / denominator; sinx = sinx + x1; i = i + 1; if(accuracy <= abs(sinval - sinx)): break; print(round(sinx)); # Driver Code n = 90; cal_sin(n); # This code is contributed by mits
C#
// C# code for implementing sin function
using System;
class GFG
{
// Function for calculating sin value
static void cal_sin(float n)
{
float accuracy = (float) 0.0001,
denominator, sinx, sinval;
// Converting degrees to radian
n = n * (float)(3.142 / 180.0);
float x1 = n;
// maps the sum along the series
sinx = n;
// holds the actual value of sin(n)
sinval = (float)Math.Sin(n);
int i = 1;
do
{
denominator = 2 * i * (2 * i + 1);
x1 = -x1 * n * n / denominator;
sinx = sinx + x1;
i = i + 1;
} while (accuracy <= sinval - sinx);
Console.WriteLine(sinx);
}
// Driver Code
static public void Main ()
{
float n = 90;
cal_sin(n);
}
}
// This code is contributed by jit_t
PHP
<?php
// PHP code for implementing sin function
// Function for calculating sin value
function cal_sin($n)
{
$accuracy = 0.0001;
// Converting degrees to radian
$n = $n * (3.142 / 180.0);
$x1 = $n;
// maps the sum along the series
$sinx = $n;
// holds the actual value of sin(n)
$sinval = sin($n);
$i = 1;
do
{
$denominator = 2 * $i * (2 * $i + 1);
$x1 = -$x1 * $n * $n / $denominator;
$sinx = $sinx + $x1;
$i = $i + 1;
} while ($accuracy <= abs($sinval - $sinx));
echo round($sinx);
}
// Main function
$n = 90;
cal_sin($n);
// This code is contributed by mits
?>
Javascript
<script>
// javascript code for implementing sin function
// Function for calculating sin value
function cal_sin(n) {
var accuracy = 0.0001, denominator, sinx, sinval;
// Converting degrees to radian
n = n * (3.142 / 180.0);
var x1 = n;
// maps the sum along the series
sinx = n;
// holds the actual value of sin(n)
sinval = Math.sin(n);
var i = 1;
do {
denominator = 2 * i * (2 * i + 1);
x1 = -x1 * n * n / denominator;
sinx = (sinx + x1);
i = i + 1;
} while (accuracy <= sinval - sinx);
document.write(sinx.toFixed(0));
}
// Main function
var n = 90;
cal_sin(n);
// This code is contributed by todaysgaurav
</script>
Producción:
1
Para función cos
Ejemplos:
Input : 30 Output : 0.86602
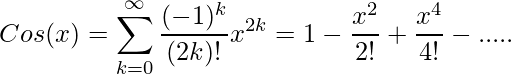
C++
// CPP code for implementing cos function
#include <iostream>
#include <math.h>
using namespace std;
// Function for calculation
void cal_cos(float n)
{
float accuracy = 0.0001, x1, denominator, cosx, cosval;
// Converting degrees to radian
n = n * (3.142 / 180.0);
x1 = 1;
// maps the sum along the series
cosx = x1;
// holds the actual value of sin(n)
cosval = cos(n);
int i = 1;
do
{
denominator = 2 * i * (2 * i - 1);
x1 = -x1 * n * n / denominator;
cosx = cosx + x1;
i = i + 1;
} while (accuracy <= fabs(cosval - cosx));
cout << cosx;
}
// Main function
int main()
{
float n = 30;
cal_cos(n);
}
Java
// Java code for implementing cos function
import static java.lang.Math.cos;
class GFG {
// Function for calculation
static void cal_cos(float n) {
float accuracy = (float) 0.0001, x1, denominator, cosx, cosval;
// Converting degrees to radian
n = n * (float) (3.142 / 180.0);
x1 = 1;
// maps the sum along the series
cosx = x1;
// holds the actual value of sin(n)
cosval = (float) cos(n);
int i = 1;
do {
denominator = 2 * i * (2 * i - 1);
x1 = -x1 * n * n / denominator;
cosx = cosx + x1;
i = i + 1;
}
while (accuracy <= cosval - cosx);
System.out.println(cosx);
}
// Main function
public static void main(String[] args) {
float n = 30;
cal_cos(n);
}
}
Python3
# Python 3 code for implementing cos function
from math import fabs, cos
# Function for calculation
def cal_cos(n):
accuracy = 0.0001
# Converting degrees to radian
n = n * (3.142 / 180.0)
x1 = 1
# maps the sum along the series
cosx = x1
# holds the actual value of sin(n)
cosval = cos(n)
i = 1
denominator = 2 * i * (2 * i - 1)
x1 = -x1 * n * n / denominator
cosx = cosx + x1
i = i + 1
while (accuracy <= fabs(cosval - cosx)):
denominator = 2 * i * (2 * i - 1)
x1 = -x1 * n * n / denominator
cosx = cosx + x1
i = i + 1
print('{0:.6}'.format(cosx))
# Driver Code
if __name__ == '__main__':
n = 30
cal_cos(n)
# This code is contributed by
# Sahil_Shelangia
C#
// C# code for implementing cos function
using System;
class GFG {
// Function for calculation
static void cal_cos(float n) {
float accuracy = (float) 0.0001, x1, denominator, cosx, cosval;
// Converting degrees to radian
n = n * (float) (3.142 / 180.0);
x1 = 1;
// maps the sum along the series
cosx = x1;
// holds the actual value of sin(n)
cosval = (float) Math.Cos(n);
int i = 1;
do {
denominator = 2 * i * (2 * i - 1);
x1 = -x1 * n * n / denominator;
cosx = cosx + x1;
i = i + 1;
}
while (accuracy <= cosval - cosx);
Console.WriteLine(cosx);
}
// Main function
static void Main() {
float n = 30;
cal_cos(n);
}
}
// This code is contributed by mits
PHP
<?php
// PHP code for implementing cos function
// Function for calculation
function cal_cos($n)
{
$accuracy = 0.0001;
// Converting degrees to radian
$n = $n * (3.142 / 180.0);
$x1 = 1;
// maps the sum along the series
$cosx = $x1;
// holds the actual value of sin(n)
$cosval = cos($n);
$i = 1;
do
{
$denominator = 2 * $i * (2 * $i - 1);
$x1 = -$x1 * $n * $n / $denominator;
$cosx = $cosx + $x1;
$i = $i + 1;
} while ($accuracy <= abs($cosval - $cosx));
echo round($cosx, 6);
}
// Driver Code
$n = 30;
cal_cos($n);
// This code is contributed by mits
?>
Javascript
<script>
// JavaScript code for implementing cos function
// Function for calculation
function cal_cos(n)
{
let accuracy = 0.0001, x1, denominator, cosx, cosval;
// Converting degrees to radian
n = n * (3.142 / 180.0);
x1 = 1;
// maps the sum along the series
cosx = x1;
// holds the actual value of sin(n)
cosval = Math.cos(n);
let i = 1;
do
{
denominator = 2 * i * (2 * i - 1);
x1 = -x1 * n * n / denominator;
cosx = cosx + x1;
i = i + 1;
} while (accuracy <= Math.abs(cosval - cosx));
document.write(cosx.toFixed(5));
}
// Main function
let n = 30;
cal_cos(n);
// This code is contributed by Surbhi Tyagi.
</script>
Producción:
0.86602
Este artículo es una contribución de Sakshi Tiwari . Si te gusta GeeksforGeeks (¡sabemos que te gusta!) y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA