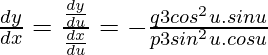Tangentes y Normales

Para una curva dada, la tangente en un punto particular es una línea recta que toca esa curva en ese punto, y va en la misma dirección que la curva en ese punto, es decir, si la curva deja de seguir la función en este punto, entonces seguirá ir recto y eso sería una línea tangente.

Entendamos esto con un ejemplo:

Imagina que estás girando una piedra en un círculo que está atada a un hilo.

Ahora, si en algún momento sueltas el hilo, la piedra seguirá un camino recto, y ese camino recto es la tangente al punto de contacto entre el camino circular y la piedra cuando se suelta la piedra. 

Propiedades de una tangente

1. Las tangentes solo tocan la curva en el punto de contacto.
2. Si cualquier tangente a una curva y = f(x) forma un ángulo θ con el eje x, entonces dy/dx = pendiente de la tangente = tan θ.
3. Si la pendiente de la tangente es cero, entonces tan θ será igual a 0, por lo que θ = 0, lo que implica que la línea tangente es paralela al eje x.
4. Si θ = π/2, entonces tan θ se aproximará a ∞, es decir, la recta tangente es perpendicular al eje x.

Aplicaciones de tangentes

1. Si viaja en automóvil en una esquina y si realiza un derrape, su automóvil comienza a patinar, continuará en una dirección tangente a la curva.
2. Si sostienes una piedra y la haces girar en un movimiento circular y luego la sueltas, volará en una tangente al movimiento circular.

Puntos importantes:

• La longitud de la tangente es 
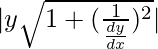
• La longitud de la subtangente es |y/dy/dx|
• Cuando una tangente es paralela a la recta ax + by + c = 0, entonces dy/dx = -a/b.

Normales: Una línea normal a una curva es una línea recta que es perpendicular a la tangente de esa curva en un punto dado.

Por ejemplo: Tomemos la curva y = x², si queremos dibujar la línea normal en el punto (1, 1), a la curva, primero dibujaremos la línea tangente a la curva en ese punto. Luego dibujaremos una recta perpendicular a la tangente. Se verá así.

Propiedades de una normal

1. Una línea normal en cualquier punto de un círculo siempre pasará por el centro del círculo.
2. La normal a cualquier curva siempre es perpendicular a la tangente en cualquier punto de la curva.

Aplicaciones de la normalidad

1. La fuerza centrípeta que actúa sobre un cuerpo que se mueve en un círculo siempre es normal al punto de contacto en un momento dado.
2. Los radios de una rueda son normales al borde de una rueda en cada punto donde el radio se conecta con el centro.

Ecuación de una Tangente y una Normal a una curva

Ecuación de una Tangente y una Normal a una curva en las Coordenadas Cartesianas

En un punto de la curva, la pendiente de la curva es igual a la pendiente de la tangente a la curva en ese punto. Entonces, la ecuación de una tangente se puede encontrar por el gradiente en ese punto a la curva y el punto dado de la siguiente manera:

Como sabemos que la ecuación de la recta que pasa por el punto P (x ₀ , y ₀ ) es 

y – y ₀ = m(x – x ₀ )

Aquí, m es la pendiente finita de la línea. Ahora la pendiente de la tangente a una curva dada es y = f(x) en el punto P (x ₀ , y ₀ ) es f(x ₀ )’. Entonces la ecuación de la tangente a la curva en el punto P(x ₀ , y ₀ ) será:

y – y ₀ = f(x ₀ )'(x – x ₀ )

Para la normal, como ya sabemos que la normal siempre es perpendicular a la recta tangente. Entonces la pendiente de la normal a la curva será:

-1/f(x0 ₎ ‘

Entonces, la ecuación de la normal a la curva y = f(x) en el punto (x ₀ , y ₀ ) es:

y – y ₀ = [-1/f(x ₀ )’](x – x ₀ )

o 

f(x ₀ )'(y – y ₀ ) + (x – x ₀ ) = 0

Ecuación de una Tangente y una Normal a una curva en Forma Paramétrica

Supongamos que la forma paramétrica de la curva es

x = x(t) ….(yo)

y = y(t) ….(ii)

Ahora encontramos la pendiente de la tangente a una curva en el punto (x ₀ , y ₀ ), usando la regla de diferenciación:

m = tan α = y _t ‘/x _t ‘

Por lo tanto, la ecuación de la tangente es:

y – y ₀ = y _t ‘/x _t ‘(x – x ₀ )

Por lo tanto, la ecuación de la normal es:

y – y ₀ = – x _t ‘/y _t ‘(x – x ₀ )

o 

y’t (y – y ₀ ) + _{x’t ( x} – x ₀ ) = 0

Ecuación de una Tangente y una Normal a una curva en Coordenadas Polares

Supongamos que la ecuación polar de la curva es r = f(θ). Representa la dependencia del radio vector r del ángulo polar θ. En coordenadas cartesianas, esta curva se puede escribir en las siguientes ecuaciones

x = r = f(θ) cosθ ….(i)

y = r = f(θ)senθ ….(ii)

Entonces, obtenemos la ecuación paramétrica de la curva. Ahora encontramos la pendiente de la tangente a una curva en el punto (x ₀ , y ₀ ).

m = tanθ = y’ _θ / x’ _θ   = r’ _θ sen θ + rcosθ/r’ _θ cosθ – rsinθ

Por lo tanto, la ecuación de la tangente es:

y – y ₀ = y’ _θ / x’ _θ (x – x ₀ )

Por lo tanto, la ecuación de la normal es:

y – y ₀ = – x’ _θ /y’ _θ (x – x ₀ )

o 

y’ _θ (y – y ₀ ) + x’ _θ (x – x ₀ ) = 0

Problemas de muestra

Pregunta 1. Encuentra la pendiente de la tangente y la normal a la curva y = 6x ² – 10x en x = 1.

Solución:

La curva dada es y = 6x ² – 10x

Ahora el gradiente, dy/dx = 12x − 10

Entonces, la pendiente de la tangente a la curva dada en x = 1 es,

dy/dx] _x=1 = 12 * 1 – 10 = 2

La pendiente de la normal será:

= -1/2 = -0,5

Pregunta 2. Encuentra la pendiente de la tangente y normal a la curva y = 3x ³ + 3sin(x) en x = 0.

Solución:

La curva dada es y = 3x ³ + 3sin(x)

Ahora el gradiente, dy/dx = 9x ² + 3cos(x) 

Entonces, la pendiente de la tangente a la curva dada en x = 0 es,

dy/dx] _x=0 = 0 + 3 * 1 = 3

La pendiente de la normal será:

= -1/3

Pregunta 3. Encuentra la ecuación de la tangente a la curva y = 6x ² – 2x + 3 en P(1, 0).

Solución:

La curva dada es y = 6x ²– 2x + 3 

Ahora el gradiente, dy/dx = 12x – 2

Entonces, la pendiente de la tangente a la curva dada en P(1,0) es 

dy/dx] _1,0 = 12 – 2 = 10

La ecuación de la recta será:

y-0 = 10(x-1)

y = 10x – 10

Pregunta 4. Determine el punto en la curva y = 6x ² – 8x + 1 donde la tangente es paralela a la línea y = 4x – 5.

Solución:

La curva dada es y = 6x ²– 8x + 1

Ahora el gradiente, dy/dx = 12x – 8

La tangente es paralela a y = 4x – 5

asi que,

12x ₀ – 8 = 4

o x ₀ = 1

Poniendo x = 1 en la ecuación de la curva 

Obtenemos, 

y ₀ = 6 – 8 + 1

y ₀ = -1

Entonces el punto es (1, -1)

Pregunta 5. Encuentra la pendiente de la tangente a la curva dada por:

x = sen ² u, y = cos ² u en el punto donde u = π/2.

Solución:

Dado: 

x = psin ³ u …(i)

y = qcos ³ u …(ii)

El valor de u = π/2

Al diferenciar las ecuaciones (i) y (ii), con respecto a u, obtenemos

dx/du = 3psin ² u.cosu …(iii)

dy/du = -3qcos ² u.sinu …(iv) 

Ahora encontramos la pendiente de la tangente en el punto u = π/2

dy/dx = -qcosu/psinu

dy/dx] _u=π/2 = -qcos(π/2)/psin(π/2) = 0

Por lo tanto, la ecuación de la tangente es y = 0.